डीएसपी - सिग्नल कनवल्शन पर संचालन
टाइम डोमेन में दो सिग्नलों का कनवल्शन फ़्रीक्वेंसी डोमेन में उनके प्रतिनिधित्व के गुणन के बराबर है। गणितीय रूप से, हम दो संकेतों के दृढ़ संकल्प को लिख सकते हैं
$ $ y (t) = x_ {1} (t) * x_ {2} (t) $ $ $ $ = \ int _ {- \ infty} ^ {\ infty} x_ {1} (p) .x_ / 2 } (टीपी) डी पी $$दृढ़ संकल्प के लिए कदम
- संकेत x 1 (t) लें और t = p को वहां रखें ताकि वह x 1 (p) हो जाए।
- सिग्नल x 2 (t) लें और चरण 1 करें और इसे x 2 (p) करें।
- सिग्नल को फोल्ड करना यानी x 2 (-p)।
- उपरोक्त संकेत x 2 [- (pt)] का समय परिवर्तन
- फिर दोनों संकेतों का गुणा करें। अर्थात $ x_ {1} (p) .x_ {2} [- (p _ t)] $
उदाहरण
आइए हम एक स्टेप सिग्नल u (t) का कनवल्शन अपनी तरह से करें।
$ y (t) = u (t) * u (t) $
$ = \ int _ {- \ infty} ^ {\ infty} [u (p) .u [- (pt)] $
अब यह टी शून्य से अधिक या उससे कम हो सकती है, जो नीचे दिए गए आंकड़ों में दिखाए गए हैं
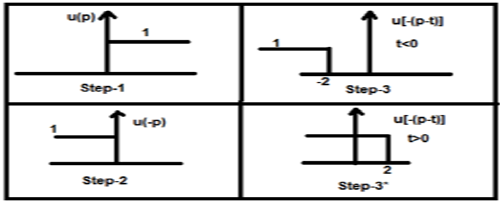
तो, उपरोक्त मामले के साथ, परिणाम निम्न संभावनाओं के साथ उत्पन्न होता है
$ y (t) = \ start {case} 0, और if \ quad t <0 \\\ int_ {0} ^ {t} 1dt, और for \ quad t> 0 \ end {केस} $
$ = \ शुरू {मामलों} 0, और अगर \ क्वाड टी <0 \\ टी, और टी> 0 \ अंत {मामलों} = आर (टी) $
बातचीत के गुण
विनिमेय
इसमें कहा गया है कि सजा का आदेश कोई मायने नहीं रखता, जिसे गणितीय रूप से दिखाया जा सकता है
$ $ x_ {1} (t) * x_ {2} (t) = x_ {2} (t) * x_ {1} (t) $$जोड़नेवाला
इसमें कहा गया है कि तीन संकेतों को शामिल करते हुए सजा का आदेश कुछ भी हो सकता है। गणितीय रूप से, इसे इस रूप में दिखाया जा सकता है;
$ $ x_ {1} (t) * [x_ {2} (t) * x_ {3} (t)] = [x_ {1} (t) * x_ {2} (t)] * x_ {3} (टी) $$विभाजित करनेवाला
दो संकेतों को पहले जोड़ा जा सकता है, और फिर उनका संकेत तीसरे संकेत को बनाया जा सकता है। यह तीसरे संकेत के साथ व्यक्तिगत रूप से दो संकेतों के दृढ़ीकरण के बराबर है और अंत में जोड़ा गया है। गणितीय रूप से, इसे इस प्रकार लिखा जा सकता है;
$ $ x_ {1} (t) * [x_ {2} (t) + x_ {3} (t)] = [x_ {1} (t) * x_ {2} (t) + x_ {1} ( टी) * x_ {3} (टी)] $$क्षेत्र
यदि एक संकेत दो संकेतों के दृढ़ीकरण का परिणाम है तो संकेत का क्षेत्र उन व्यक्तिगत संकेतों का गुणन है। गणितीय रूप से यह लिखा जा सकता है
यदि $ y (t) = x_ {1} * x_ {2} (t) $
फिर, y के क्षेत्र (टी) = एक्स के क्षेत्र 1 (टी) एक्स के एक्स क्षेत्र 2 (टी)
स्केलिंग
यदि दो संकेतों को कुछ अज्ञात निरंतर "और" के लिए स्केल किया जाता है, तो परिणामी संकेत भी उसी निरंतर "ए" के लिए दृढ़ हो जाएगा और उस मात्रा से विभाजित किया जाएगा जैसा कि नीचे दिखाया गया है।
यदि, $ x_ {1} (t) * x_ {2} (t) = y (t) $
फिर, $ x_ {1} (पर) * x_ {2} (पर) = \ frac {y (पर)} {a}, a \ ne 0 $
विलंब
मान लीजिए कि एक संकेत y (t) दो संकेतों X1 (t) और x2 (t) के दृढ़ संकल्प का परिणाम है। यदि दो संकेतों को क्रमशः समय t1 और t2 द्वारा विलंबित किया जाता है, तो परिणामी संकेत y (t) देरी से (t1 + t2) होगा। गणितीय रूप से, इसे इस प्रकार लिखा जा सकता है -
यदि, $ x_ {1} (t) * x_ {2} (t) = y (t) $
फिर, $ x_ {1} (t-t_ {1}) * x_ {2} (t-t_ {2}) = y [t- (t_ {1} + t_ {2}]] $
हल के उदाहरण
Example 1 - संकेतों u (t-1) और u (t-2) के दृढ़ संकल्प का पता लगाएं।
Solution- दिए गए संकेत यू (टी -1) और यू (टी -2) हैं। उनका कनविक्शन नीचे दिखाए अनुसार किया जा सकता है -
$ y (t) = u (t-1) * u (t-२) $
$ y (t) = \ int _ {- \ infty} ^ {+ \ infty} [u (t-1) .u (टी -2)] dt $।
$ = आर (टी -1) + आर (टी -2) $
$ = आर (टी -3) $
Example 2 - द्वारा दिए गए दो संकेतों के दृढ़ संकल्प का पता लगाएं
$x_{1}(n) = \lbrace 3,-2, 2\rbrace $
$ x_ {2} (n) = \ start {मामलों} 2, और 0 \ leq n \ leq 4 \\ 0, & x> कहीं और \ अंत {मामलों} $
Solution -
x 2 (n) को $ x_ {2} (n) = \ lbrace 2,2,2,2,2 \ rbrace के रूप में डीकोड किया जा सकता है
x 1 (n) को पहले $ = \ lbrace 3, -2,3 \ rbrace = 3-2Z ^ {- 1} + 2Z ^ {- 2} $ दिया जाता है
इसी तरह, $ x_ {2} (z) = 2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {- 4} $
परिणामी संकेत,
$ X (Z) = X_ {1} (Z) X_ {2} (z) $
$ = \ lbrace 3-2Z ^ {- 1} + 2Z ^ {- 2} \ rbrace \ टाइम्स \ lbrace 2 + 2Z ^ {- 1} + 2Z ^ {- 2} + 2Z ^ {- 3} + 2Z ^ {-4} \ rbrace $
$ = 6 + 2Z ^ {- 1} + 6Z ^ {- 2} + 6Z ^ {- 3} + 6Z ^ {- 4} + 6Z ^ {- 5} $
उपरोक्त के Z- परिवर्तन को उलटते हुए, हमें परिणामी संकेत मिलेगा
$ x (n) = \ lbrace 6,2,6,6,6,0,4 \ rbrace $ उत्पत्ति पहली बार में
Example 3 - निम्नलिखित 2 संकेतों के दृढ़ संकल्प का निर्धारण करें -
$x(n) = \lbrace 2,1,0,1\rbrace$
$h(n) = \lbrace 1,2,3,1\rbrace$
Solution -
संकेतों के जेड-परिवर्तन को लेते हुए, हम प्राप्त करते हैं,
$ x (z) = 2 + 2Z ^ {- 1} + 2Z ^ {- 3} $
और $ h (n) = 1 + 2Z ^ {- 1} + 3Z ^ {- 2} + Z ^ {- 3} $
अब दो सिग्नल के दोषी होने का मतलब है उनके जेड-ट्रांसफॉर्मेशन का गुणा
वह $ Y (Z) = X (Z) \ गुना h (Z) $ है
$ = \ lbrace 2 + 2Z ^ {- 1} + 2Z ^ {- 3} \ rbrace \ टाइम्स \ lbrace 1 + 2Z ^ {- 1} + 3Z ^ {- 2} + Z ^ {- 3} \ rbrace $
$ = \ lbrace 2 + 5Z ^ {- 1} + 8Z ^ {- 2} + 6Z ^ {- 3} + 3Z ^ {- 4} + 3Z ^ {- 5} + Z ^ {- 6} \ r \ _ $
उलटा Z- परिवर्तन लेते हुए, परिणामी संकेत के रूप में लिखा जा सकता है;
$ y (n) = \ lbrace 2,5,8,6,6,1 \ rbrace ओरिजिनल $