डिजिटल सिग्नल प्रोसेसिंग - सिग्नल-डेफिनिशन

परिभाषा

कुछ भी जो सूचना को वहन करता है उसे संकेत कहा जा सकता है। इसे एक भौतिक मात्रा के रूप में भी परिभाषित किया जा सकता है जो समय, तापमान, दबाव या किसी स्वतंत्र चर जैसे कि भाषण संकेत या वीडियो सिग्नल के साथ बदलता रहता है।

ऑपरेशन की प्रक्रिया जिसमें एक संकेत की विशेषताएं (आयाम, आकार, चरण, आवृत्ति, आदि) एक परिवर्तन से गुजरती हैं उन्हें सिग्नल प्रोसेसिंग के रूप में जाना जाता है।

Note- मुख्य संकेत के साथ हस्तक्षेप करने वाले किसी भी अवांछित सिग्नल को शोर कहा जाता है। तो, शोर भी एक संकेत है लेकिन अवांछित है।

उनके प्रतिनिधित्व और प्रसंस्करण के अनुसार, संकेतों को विभिन्न श्रेणियों के विवरणों में वर्गीकृत किया जा सकता है, जिनके बारे में नीचे चर्चा की गई है।

निरंतर समय संकेत

निरंतर-समय संकेतों को समय की एक निरंतरता के साथ परिभाषित किया जाता है और इस प्रकार, एक निरंतर स्वतंत्र चर द्वारा दर्शाया जाता है। निरंतर-समय संकेतों को अक्सर एनालॉग संकेतों के रूप में संदर्भित किया जाता है।

इस प्रकार का संकेत आयाम और समय दोनों में निरंतरता दर्शाता है। प्रत्येक समय में इनका मान होगा। निरंतर समय संकेत के साइन और कोसाइन कार्य सबसे अच्छे उदाहरण हैं।

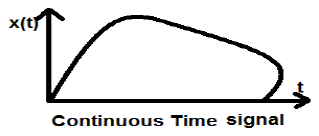
ऊपर दिखाया गया संकेत निरंतर समय संकेत का एक उदाहरण है क्योंकि हम प्रत्येक पल में संकेत का मूल्य प्राप्त कर सकते हैं।

असतत समय संकेत

असतत समय पर परिभाषित होने वाले संकेतों को असतत संकेतों के रूप में जाना जाता है। इसलिए, प्रत्येक स्वतंत्र चर का अलग मूल्य है। इस प्रकार, उन्हें संख्याओं के अनुक्रम के रूप में दर्शाया जाता है।

यद्यपि भाषण और वीडियो संकेतों को निरंतर और असतत समय प्रारूप दोनों में प्रतिनिधित्व करने का विशेषाधिकार है; कुछ परिस्थितियों में, वे समान हैं। एम्पलीट्यूड भी असतत विशेषताओं को दर्शाता है। इसका सटीक उदाहरण एक डिजिटल सिग्नल है; जिसका आयाम और समय दोनों असतत हैं।

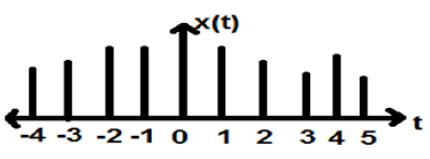
समय के ऊपर एक असतत संकेत के असतत आयाम की विशेषता दर्शाती है। गणितीय रूप से, इन प्रकार के संकेतों को औपचारिक रूप दिया जा सकता है;

$ $ x = \ left \ {x \ left [n \ right] \ right \}, \ quad - \ infty <n <\ infty $$

जहाँ, n एक पूर्णांक है।

यह संख्या x का एक क्रम है, जहाँ अनुक्रम में n ^वें नंबर को x [n] के रूप में दर्शाया जाता है।