डीएसपी - डीटी सिग्नल का वर्गीकरण
कंटीन्यू टाइम सिग्नल की तरह, डिसक्रीट टाइम सिग्नल को सिग्नल पर स्थितियां या संचालन के अनुसार वर्गीकृत किया जा सकता है।
सम और विषम संकेत
यहां तक कि सिग्नल भी
एक संकेत को सममित या सममित कहा जाता है यदि यह निम्नलिखित स्थिति को संतुष्ट करता है;
$ $ x (-n) = x (n) $ $
यहाँ, हम देख सकते हैं कि x (-1) = x (1), x (-2) = x (2) और x (-n) = x (n)। इस प्रकार, यह एक भी संकेत है।
अजीब संकेत
एक संकेत को विषम कहा जाता है यदि यह निम्नलिखित स्थिति को संतुष्ट करता है;
$ $ x (-n) = -x (n) $ $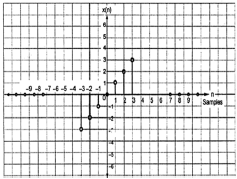
आकृति से, हम देख सकते हैं कि x (1) = -x (-1), x (2) = -x (2) और x (n) = -x (-n)। इसलिए, यह एक विषम और साथ ही एंटी-सममित संकेत है।
आवधिक और गैर-आवधिक संकेत
एक असतत समय संकेत आवधिक है और केवल अगर यह निम्न स्थिति को संतुष्ट करता है -
$ $ x (n + N) = x (n) $ $यहाँ, x (n) सिग्नल N अवधि के बाद खुद को दोहराता है। यह एक कोसाइन सिग्नल पर विचार करके सबसे अच्छा समझा जा सकता है -
$ $ x (n) = A \ cos (2 \ pi f_ {0} n + \ थीटा) $ $ $ $ x (n + N) = A \ cos (2 \ pi f_ {0} (n + N) + \ Theta) = A \ cos (2 \ pi f_ {0} n + 2 \ pi f_ {0} N + \ थीटा) $ $ $ $ = A \ cos (2 \ pi f_ {0} n + 2 \ _ pi f_) {0} एन \ थीटा) $$संकेत के लिए आवधिक बनने के लिए, निम्नलिखित स्थिति को संतुष्ट किया जाना चाहिए;
$ $ x (n + N) = x (n) $ $ $ $ \ Rightarrow A \ cos (2 \ pi f_ {0} n + 2 \ pi f_ {0} N + \ थीटा) = A \ cos (2 \ _) pi f_ {0} n + \ थीटा) $$यानी $ 2 \ pi f_ {0} N $ $ 2 \ pi $ का एक अभिन्न गुण है
$ $ 2 \ pi f_ {0} N = 2 \ pi K $$ $ $ \ Rightarrow N = \ frac {K} {f_ {0}} $ $असतत साइनसोइडल संकेतों की आवृत्ति को $ 2 \ pi $ के अभिन्न कई द्वारा अलग किया जाता है।
ऊर्जा और पावर सिग्नल
ऊर्जा संकेत
असतत समय संकेत की ऊर्जा को ई। गणितीय रूप में निरूपित किया जाता है, इसे इस प्रकार लिखा जा सकता है;
$ $ E = \ displaystyle \ sum \ limit_ {n = - \ infty} ^ {+ \ infty} | x (n) | ^ 2 $$यदि $ x (n) $ के प्रत्येक व्यक्तिगत मान को चुकता और जोड़ा जाता है, तो हमें ऊर्जा संकेत मिलता है। यहाँ $ x (n) $ ऊर्जा संकेत है और इसकी ऊर्जा समय के साथ परिमित होती है अर्थात $ 0 <E <\ infty $
पावर सिग्नल
असतत संकेत की औसत शक्ति को पी। गणितीय रूप में दर्शाया जाता है, इसे इस प्रकार लिखा जा सकता है;
$ $ P = \ lim_ {N \ to \ infty} \ frac {1} {2N + 1} \ displaystyle \ sum \ limit_ {n = -N} ^ {+ N} | x (n) | ^ 2 $ $यहाँ, शक्ति परिमित है अर्थात 0 <P <ite। हालांकि, कुछ संकेत हैं, जो न तो ऊर्जा और न ही बिजली प्रकार के संकेत से संबंधित हैं।