डीएसपी - विविध संकेत
अन्य संकेत हैं, जो उन पर किए गए ऑपरेशन का परिणाम हैं। कुछ सामान्य प्रकार के संकेतों की चर्चा नीचे की गई है।
संयुग्म संकेत
सिग्नल, जो स्थिति को संतुष्ट करते हैं $ x (t) = x * (- t) $ को संयुग्म संकेत कहा जाता है।
आज्ञा देना $ x (t) = a (t) + jb (t) $ ... eqn। 1
तो, $ x (-t) = (-t) + jb (-t) $
और $ x * (- t) = (a -t) -jb (-t) $ ... eqn। 2
शर्त के अनुसार, $ x (t) = x * (- t) $
यदि हम व्युत्पन्न समीकरण 1 और 2 दोनों की तुलना करते हैं, तो हम देख सकते हैं कि वास्तविक भाग सम है, जबकि काल्पनिक भाग विषम है। यह एक संकेत प्रकार के संयुग्मित होने की स्थिति है।
Conjugate एंटी-सिमेट्रिक सिग्नल
सिग्नल, जो स्थिति को संतुष्ट करते हैं $ x (t) = -x * (- t) $ को संयुग्म विरोधी सममित संकेत कहा जाता है
आज्ञा देना $ x (t) = a (t) + jb (t) $ ... eqn। 1
तो $ x (-t) = (-t) + jb (-t) $
और $ x * (- t) = (a -t) -jb (-t) $
$ -x * (- t) = -a (-t) + jb (-t) $ ... eqn। 2
शर्त के अनुसार $ x (t) = -x * (- t) $
अब, फिर से तुलना करें, दोनों समीकरण उसी तरह जैसे हमने संकेतों को संयुग्मित करने के लिए किया था। यहां, हम पाएंगे कि वास्तविक भाग विषम है और काल्पनिक भाग सम है। यह एक संकेत के लिए संयुग्म विरोधी सममित प्रकार बनने की स्थिति है।
उदाहरण
बता दें कि दिया गया संकेत $ x (t) = \ sin t + jt ^ {2} $ है।
यहाँ, वास्तविक भाग $ \ sin t $ विषम है और काल्पनिक भाग $ t ^ 2 $ है। तो, इस संकेत को संयुग्म विरोधी सिमेट्रिक संकेत के रूप में वर्गीकृत किया जा सकता है।
किसी भी फ़ंक्शन को दो भागों में विभाजित किया जा सकता है। एक भाग संयुग्म समरूपता और अन्य भाग संयुग्म विरोधी समरूप हो रहा है। तो किसी भी संकेत x (t) के रूप में लिखा जा सकता है
$ $ x (t) = xcs (t) + xcas (t) $ $जहाँ $ xcs (t) $ संयुग्म सममित संकेत है और $ xcas (t) $ संयुग्म विरोधी सममित संकेत है
$ $ xcs (t) = \ frac {[x (t) + x * ((t)]} {२} $ $तथा
$ $ xcas (t) = \ frac {[x (t) -x * (- t)]} {२} ५%हाफ वेव सिमेट्रिक सिग्नल
जब कोई सिग्नल $ cx (t) = -x (t \ pm (\ frac {T_ {0}} {2}) $) को संतुष्ट करता है, तो इसे आधा तरंग सममित संकेत कहा जाता है। यहां, सिग्नल के आयाम उलट और समय की शिफ्टिंग आधे समय तक होती है। आधा लहर सममित संकेत के लिए, औसत मूल्य शून्य होगा लेकिन स्थिति उलट होने पर ऐसा नहीं है।
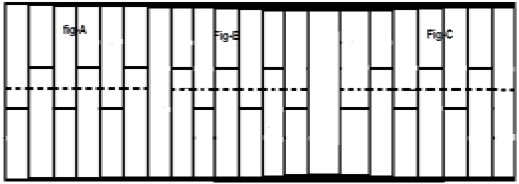
एक संकेत एक्स (टी) पर विचार करें जैसा कि ऊपर ए में दिखाया गया है। पहला कदम सिग्नल को शिफ्ट करने और इसे $ x [t - (\ frac {T} {2})] $ बनाने का है। तो, नया संकेत बदल जाता है जैसा कि आंकड़ा बी में दिखाया गया है। अगला, हम सिग्नल के आयाम को उल्टा करते हैं, अर्थात इसे $ -x [t - (\ frac {T} {2})] $ जैसा कि चित्र C में दिखाया गया है। चूंकि, यह सिग्नल आधे समय के स्थानांतरण और आयाम के उलट होने के बाद खुद को दोहराता है, यह एक आधा लहर सममित संकेत है।
ऑर्थोगोनल सिग्नल
दो संकेतों x (t) और y (t) को ऑर्थोगोनल कहा जाता है यदि वे निम्नलिखित दो स्थितियों को पूरा करते हैं।
Condition 1 - $ \ int _ {- \ infty} ^ {\ infty} x (t) y (t) = 0 $ [गैर-आवधिक संकेत के लिए]
Condition 2 - $ \ int x (t) y (t) = 0 $ [आवधिक संकेत के लिए]
सिग्नल, जिसमें विषम हार्मोनिक्स (3 आरडी , 5 वें , 7 वें ... आदि) होते हैं और अलग-अलग आवृत्तियों होते हैं, एक दूसरे के लिए पारस्परिक रूप से ऑर्थोगोनल होते हैं।
त्रिकोणमितीय प्रकार के संकेतों में, साइन फ़ंक्शंस और कोज़ाइन फ़ंक्शंस एक-दूसरे के लिए ऑर्थोगोनल भी हैं; बशर्ते, उनकी आवृत्ति समान हो और एक ही चरण में हों। उसी तरह डीसी (डायरेक्ट करंट सिग्नल) और साइनसोइडल सिग्नल भी एक दूसरे के लिए ऑर्थोगोनल हैं। यदि x (t) और y (t) दो ऑर्थोगोनल सिग्नल हैं और $ z (t) = x (t) + y (t) $ हैं तो z (t) की शक्ति और ऊर्जा को लिखा जा सकता है;
$ $ P (z) = p (x) + p (y) $$ $$ E (z) = E (x) + E (y) $ $उदाहरण
संकेत का विश्लेषण करें: $ z (t) = 3 + 4 \ sin (2 \ pi t + 30 ^ 0) $
यहां, संकेत में डीसी सिग्नल (3) और एक साइन फ़ंक्शन शामिल हैं। इसलिए, संपत्ति द्वारा यह संकेत एक ऑर्थोगोनल सिग्नल है और इसमें दो उप-सिग्नल परस्पर एक-दूसरे के लिए ऑर्थोगोनल हैं।