डीएसपी - फास्ट फूरियर ट्रांसफॉर्म
पहले के डीएफटी तरीकों में, हमने देखा है कि कम्प्यूटेशनल भाग बहुत लंबा है। हम इसे कम करना चाहते हैं। यह एफएफटी या तेज फूरियर ट्रांसफॉर्म के माध्यम से किया जा सकता है। तो, हम कह सकते हैं कि FFT एक एल्गोरिथम प्रारूप में असतत फूरियर रूपांतरण की गणना के अलावा कुछ भी नहीं है, जहां कम्प्यूटेशनल भाग कम हो जाएगा।
एफएफटी होने का मुख्य लाभ यह है कि इसके माध्यम से हम एफआईआर फिल्टर डिजाइन कर सकते हैं। गणितीय रूप से, एफएफटी को निम्नानुसार लिखा जा सकता है;
$ $ x [K] = \ displaystyle \ sum \ limit_ {n = 0} ^ {N-1} x [n] W_N ^ {nk} $$इसे बेहतर तरीके से समझने के लिए एक उदाहरण लेते हैं। हमने $ x_0 \ quad से \ quad x_7 $ नाम के आठ बिंदुओं पर विचार किया है। हम एक समूह में समान शब्द और दूसरे में विषम शब्द चुनेंगे। ऊपर कहा गया है की आरेखीय दृश्य नीचे दिखाया गया है -
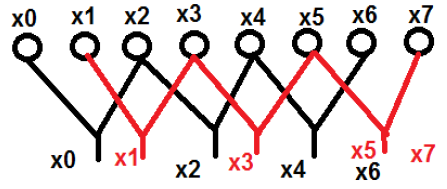
यहाँ, अंक x 0 , x 2 , x 4 और x 6 को एक श्रेणी में रखा गया है और इसी तरह, अंक x 1 , x 3 , x 5 और x 7 को अन्य श्रेणी में रखा गया है। अब, हम उन्हें दो के समूह में आगे बना सकते हैं और संगणना के साथ आगे बढ़ सकते हैं। अब, आइए देखें कि कैसे आगे के दो हिस्सों में टूटने से गणना में मदद मिल रही है।
$ x [k] = \ displaystyle \ sum \ limit_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_N ^ {2rk} + \ displaystyle \ sum \ limit_ r = 0 } ^ {\ frac {एन} {2} -1} एक्स [2R + 1] W_N ^ {(2R +1) कश्मीर} $
$ = \ sum_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_ {N / 2} ^ {rk} + \ sum_ {r = 0} ^ {\ frac {N } {2} -1} x [2r + 1] W_ {N / 2} ^ {rk} \ टाइम्स W_N ^ K $
$ = G [k] + H [k] \ टाइम्स W_N ^ k $
प्रारंभ में, हमने आठ-बिंदु क्रम लिया, लेकिन बाद में हमने उस एक को दो भागों में तोड़ दिया [जी] और एच [के]। जी [के] का अर्थ सम भाग के लिए है जबकि एच [के] विषम भाग के लिए है। यदि हम इसे आरेख के माध्यम से महसूस करना चाहते हैं, तो इसे नीचे दिखाया जा सकता है -
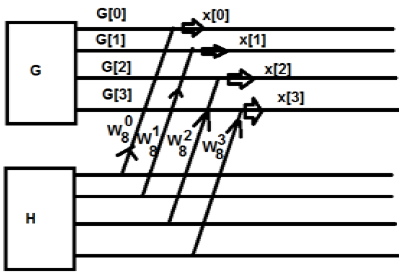
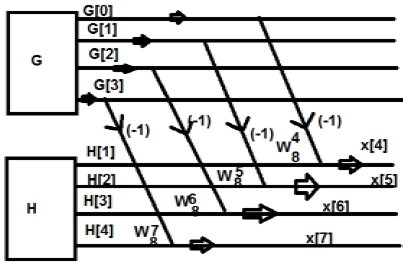
उपरोक्त आंकड़े से, हम यह देख सकते हैं
$ W_8 ^ 4 = -1 $
$ W_8 ^ 5 = -W_8 ^ 1 $
$ W_8 ^ 6 = -W_8 ^ 2 $
$ W_8 ^ 7 = -W_8 ^ 3 $
इसी प्रकार, अंतिम मान निम्न प्रकार लिखे जा सकते हैं -
$ G [0] -H [0] = x [4] $
$ G [1] -W_8 ^ 1H [1] = x [5] $
$ G [2] -W_8 ^ 2H [2] = x [6] $
$ G [1] -W_8 ^ 3H [3] = x [7] $
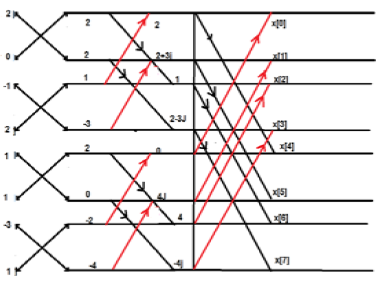
उपरोक्त एक आवधिक श्रृंखला है। इस प्रणाली का नुकसान यह है कि K को 4 बिंदु से परे नहीं तोड़ा जा सकता है। अब हम ऊपर दिए गए शब्दों को तोड़ते हैं। हम संरचनाओं को कुछ इस तरह से प्राप्त करेंगे
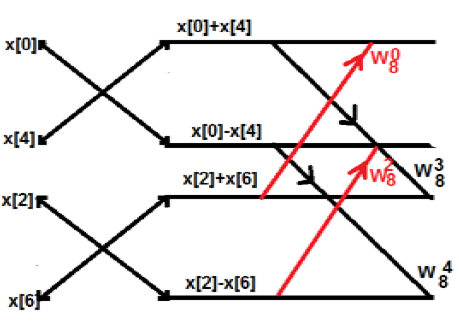
उदाहरण
अनुक्रम x [n] = {2,1, -1, -3,0,1,2,1} पर विचार करें। FFT की गणना करें।
Solution - दिया गया क्रम x [n] = {2,1, -1, -3,0,1,2,1} है
नीचे दिखाए अनुसार शब्दों को व्यवस्थित करें;