डीएसपी - इन-प्लेस कम्प्यूटेशन
FFT की गणना करने के लिए तेजी से हार्डवेयर डिजाइन करने के लिए मेमोरी का यह कुशल उपयोग महत्वपूर्ण है। इस मेमोरी उपयोग का वर्णन करने के लिए इन-प्लेस अभिकलन शब्द का उपयोग किया जाता है।
समय अनुक्रम में गिरावट
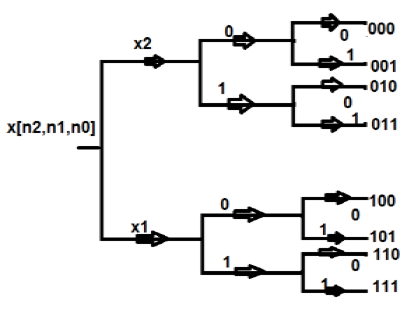
इस संरचना में, हम द्विआधारी प्रारूप में 0 और 1 में सभी बिंदुओं का प्रतिनिधित्व करते हैं। फिर, हम उन संरचनाओं को उलट देते हैं। उसके बाद जो क्रम हमें मिलता है उसे बिट रिवर्सल अनुक्रम के रूप में जाना जाता है। इसे समय क्रम में विघटन के रूप में भी जाना जाता है। एक आठ-सूत्रीय डीएफटी का इन-प्लेस संगणना एक सारणीबद्ध प्रारूप में दिखाया गया है जैसा कि नीचे दिखाया गया है -
| अंक | द्विआधारी प्रारूप | उलट | एक्वैरियम अंक |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| 7 | 111 | 111 | 7 |
फ्रीक्वेंसी सीक्वेंस में गिरावट
समय अनुक्रम के अलावा, एन-पॉइंट अनुक्रम को आवृत्ति में भी दर्शाया जा सकता है। इसे बेहतर ढंग से समझने के लिए हम चार सूत्रीय क्रम लेते हैं।
अनुक्रम $ x [0], x [1], x [2], x [3], x [4], x [5], x [6], x [7] $ होने दें। हम शुरू में दो बिंदुओं को एक समूह में बाँटेंगे। गणितीय रूप से, इस क्रम को इस प्रकार लिखा जा सकता है;
$ $ x [k] = \ sum_ {n = 0} ^ {N-1} x [n] W_N ^ {n} $ $अब हम क्रम संख्या ० से ३ का एक समूह बनाते हैं और ४ से group से क्रम का एक और समूह बनाते हैं। अब, गणितीय रूप से इसे दिखाया जा सकता है;
$$ \ displaystyle \ sum \ limit_ {n = 0} ^ {\ frac {N} {2} -1} x [n] W_N ^ {nk} + \ displaystyle \ sum \ limit_ {n = N / 2} ^ {एन 1} एक्स [n] W_N ^ {} nk $$N से r को प्रतिस्थापित करते हैं, जहाँ r = 0, 1, 2…। (N / 2-1)। गणित के अनुसार,
$$ \ displaystyle \ sum \ limit_ {n = 0} ^ {\ frac {N} {2} -1} x [r] W_ {N / 2} ^ {nr} $ $हम शुरू में पहले चार अंक (x [0], x [1], x [2], x [3]) लेते हैं, और निम्नानुसार गणितीय रूप से उनका प्रतिनिधित्व करने का प्रयास करते हैं -
$ \ sum_ {n = 0} ^ 3x [n] W_8 ^ {nk} + \ sum_ {n = 0} ^ 3x [n + 4] W_8 ^ {(n + 4) k} $
$ = \ lbrace \ sum_ {n = 0} ^ 3x [n] + \ sum_ {n = 0} ^ 3x [n + 4] W_8 ^ {(4) k} \ rbrace \ टाइम्स W_8 ^ / nk} $
अब $ X [0] = \ sum_ {n = 0} ^ 3 (X [n] + X [n + 4]) $
$ X [1] = \ sum_ {n = 0} ^ 3 (X [n] + X [n + 4]) W_8 ^ {nk} $
$ = [X [0] -X [4] + (X [1] -X [5]) W_8 ^ 1 + (X [2] -X [6]) W_8 ^ 2 + (X [3] -X) [7]) W_8 ^ 3 $
हम इसे दो और भागों में तोड़ सकते हैं, जिसका अर्थ है कि उन्हें 4-बिंदु अनुक्रम के रूप में तोड़ने के बजाय, हम उन्हें 2-बिंदु अनुक्रम में तोड़ सकते हैं।