डिजिटल सिग्नल प्रोसेसिंग - मूल डीटी सिग्नल
हमने देखा है कि कंटिन्युअस टाइम डोमेन में बेसिक सिग्नल्स को कैसे दर्शाया जा सकता है। आइए हम देखें कि कैसे असतत समय डोमेन में मूल संकेतों का प्रतिनिधित्व किया जा सकता है।
यूनिट आवेग अनुक्रम
इसे असतत समय डोमेन में δ (n) के रूप में दर्शाया गया है और इसे परिभाषित किया जा सकता है;
$$ \ delta (n) = \ start {case} 1, और \ quad n = 0 \\ 0 के लिए, और अन्यथा \ end {केस} $$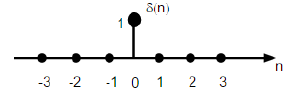
यूनिट स्टेप सिग्नल
असतत समय इकाई चरण संकेत के रूप में परिभाषित किया गया है;
$ $ U (n) = \ start {case} 1, और for \ quad n \ geq0 \\ 0, और for \ quad n <0 \ end {केस} $$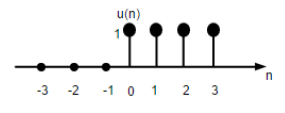
ऊपर दिया गया आंकड़ा एक असतत चरण फ़ंक्शन के चित्रमय प्रतिनिधित्व को दर्शाता है।
यूनिट रैंप फंक्शन
एक असतत इकाई रैंप फ़ंक्शन को निम्न के रूप में परिभाषित किया जा सकता है -
$ $ r (n) = \ start {case} n, और for \ quad n \ geq0 \\ 0, और for \ quad n <0 \ end {केस} $$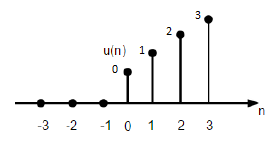
ऊपर दिया गया आंकड़ा एक असतत रैंप सिग्नल के चित्रमय प्रतिनिधित्व को दर्शाता है।
परवलयिक क्रिया
असतत इकाई परवलयिक क्रिया को p (n) के रूप में निरूपित किया जाता है और इसे परिभाषित किया जा सकता है;
$ $ p (n) = \ start {case} \ frac {n ^ {2}} {2}, और \ quad n \ geq0 \\ 0 के लिए, और \ Quad n <0 \ end {मामलों} के लिए $ $यूनिट स्टेप फ़ंक्शन के संदर्भ में इसे लिखा जा सकता है;
$ $ P (n) = \ frac {n ^ {2}} {2} U (n) $ $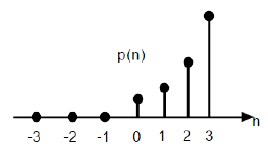
ऊपर दिया गया आंकड़ा एक परवलयिक अनुक्रम के चित्रमय प्रतिनिधित्व को दर्शाता है।
साइनसोइडल सिग्नल
सभी निरंतर-समय के संकेत आवधिक हैं। असतत समय साइनसोइडल अनुक्रम आवधिक हो सकते हैं या नहीं। वे ω के मूल्य पर निर्भर करते हैं। असतत समय संकेत समय-समय पर होने के लिए, कोणीय आवृत्ति π 2π का एक तर्कसंगत बहु होना चाहिए।
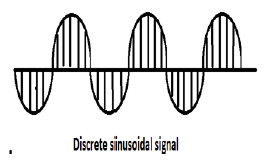
ऊपर की आकृति में एक असतत साइनसोइडल संकेत दिखाया गया है।
साइनसोइडल सिग्नल के असतत रूप को प्रारूप में दर्शाया जा सकता है -
$ $ x (n) = A \ sin (\ omega n + \ phi) $$यहाँ A, n और φ का सामान्य अर्थ है और n पूर्णांक है। असतत साइनसोइडल सिग्नल की समयावधि किसके द्वारा दी गई है -
$$ N = \ frac {2 \ pi m} {\ omega} $$जहाँ, N और m पूर्णांक हैं।