डीएसपी - सिग्नल शिफ्टिंग पर संचालन
शिफ्टिंग का अर्थ है सिग्नल की गति, या तो समय डोमेन (Y- अक्ष के आसपास) या आयाम डोमेन (X- अक्ष के आसपास) में। तदनुसार, हम शिफ्टिंग को टाइम शिफ्टिंग और एम्प्लिट्यूड शिफ्टिंग नामक दो श्रेणियों में वर्गीकृत कर सकते हैं, इन पर बाद में नीचे चर्चा की गई है।
समय बदलता है
टाइम शिफ्टिंग का मतलब है, टाइम डोमेन में सिग्नल की शिफ्टिंग। गणितीय रूप से, इसे लिखा जा सकता है
$ $ x (t) \ rightarrow y (t + k) $ $यह K मान धनात्मक हो सकता है या यह ऋणात्मक हो सकता है। K मान के संकेत के अनुसार, हमारे पास दो प्रकार की शिफ्टिंग है, जिसका नाम राइट शिफ्टिंग और लेफ्ट शिफ्टिंग है।
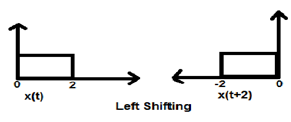
केस 1 (K> 0)
जब K शून्य से अधिक होता है, तो सिग्नल का स्थानांतरण समय डोमेन में "बाएं" की ओर होता है। इसलिए, इस प्रकार की शिफ्टिंग को सिग्नल के लेफ्ट शिफ्टिंग के रूप में जाना जाता है।
Example
केस 2 (K <0)
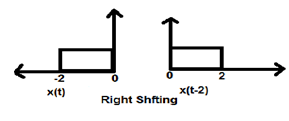
जब K शून्य से कम होता है तो सिग्नल की शिफ्टिंग टाइम डोमेन में दाईं ओर होती है। इसलिए, इस प्रकार की शिफ्टिंग को राइट शिफ्टिंग के रूप में जाना जाता है।
Example
नीचे दिया गया आंकड़ा 2 द्वारा सिग्नल के सही स्थानांतरण को दर्शाता है।
आयाम शिफ्टिंग
आयाम शिफ्टिंग का अर्थ है आयाम डोमेन में सिग्नल का स्थानांतरण (एक्स-एक्सिस के आसपास)। गणितीय रूप से, इसका प्रतिनिधित्व इस प्रकार किया जा सकता है -
$ $ x (t) \ rightarrow x (t) + K $ $यह K मान धनात्मक या ऋणात्मक हो सकता है। तदनुसार, हमारे पास दो प्रकार के आयाम स्थानांतरण हैं जिनके बारे में नीचे चर्चा की गई है।
केस 1 (K> 0)
जब K शून्य से अधिक होता है, तो सिग्नल का स्थानांतरण एक्स-अक्ष में ऊपर की ओर होता है। इसलिए, इस प्रकार के स्थानांतरण को ऊपर की ओर स्थानांतरण के रूप में जाना जाता है।
Example
आइए एक संकेत x (t) पर विचार करें जो कि दिया गया है;
$ $ x = \ शुरू {मामलों} 0, और टी <0 \\ 1, और 0 \ leq t \ leq 2 \\ 0, और टी> 0 \ अंत {मामलों} $ $हमने K = + 1 लिया है, इसलिए नए संकेत के रूप में लिखा जा सकता है -
$ y (t) \ rightarrow x (t) + 1 $ इसलिए, y (t) को अंत में लिखा जा सकता है;
$ $ x (t) = \ start {case} 1, & t <0 \\ 2, और 0 \ leq t \ leq 2 \\ 1, & t> 0 \ end {केस} $ $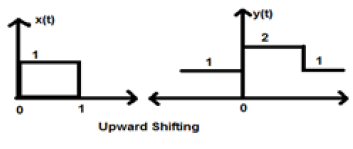
केस 2 (K <0)
जब K शून्य से कम होता है तो सिग्नल का स्थानांतरण X- अक्ष में नीचे की ओर होता है। इसलिए, इसे सिग्नल की डाउनवर्ड शिफ्टिंग कहा जाता है।
Example
आइए एक संकेत x (t) पर विचार करें जो कि दिया गया है;
$ $ x (t) = \ start {मामलों} 0, और टी <0 \\ 1, और 0 \ leq t \ leq 2 \\ 0, और t> 0 \ end {मामलों} $ $हमने K = -1 लिया है, इसलिए नए संकेत के रूप में लिखा जा सकता है;
$ y (t) \ rightarrow x (t) -1 $ इसलिए, y (t) को अंत में लिखा जा सकता है;
$ $ y (t) = \ start {case} -1, और t <0 \\ 0, & 0 \ leq t \ leq 2 \\ -1, & t> 0 \ end {केस} $$