डीएसपी - सिग्नल स्केलिंग पर संचालन
सिग्नल के स्केलिंग का मतलब है, एक स्थिर सिग्नल के समय या आयाम के साथ गुणा किया जाता है।
टाइम स्केलिंग
यदि किसी स्थिरांक को समय अक्ष से गुणा किया जाता है तो उसे टाइम स्केलिंग के रूप में जाना जाता है। इसे गणितीय रूप में दर्शाया जा सकता है;
$ x (t) \ rightarrow y (t) = x (\ Alpha t) $ या $ x (\ frac {t} {\ alpha}) $; जहां α 0
तो y- अक्ष समान होने के नाते, x- अक्ष परिमाण घटता है या स्थिर के संकेत के अनुसार बढ़ता है (चाहे सकारात्मक या नकारात्मक)। इसलिए, स्केलिंग को भी दो श्रेणियों में विभाजित किया जा सकता है जैसा कि नीचे चर्चा की गई है।
समय संपीड़न
जब भी अल्फा शून्य से अधिक होता है, सिग्नल का आयाम अल्फा से विभाजित हो जाता है जबकि Y- अक्ष का मान समान रहता है। इसे टाइम कम्प्रेशन के नाम से जाना जाता है।
Example
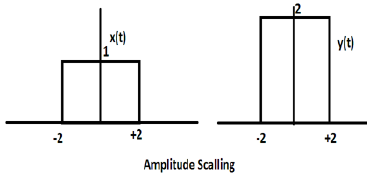
आइए एक संकेत x (t) पर विचार करें, जो नीचे दिए गए चित्र में दिखाया गया है। आइए हम अल्फा के मान को 2 के रूप में लें। तो, y (t) x (2t) होगा, जो कि दिए गए चित्र में दर्शाया गया है।

स्पष्ट रूप से, हम उपरोक्त आंकड़ों से देख सकते हैं कि y- अक्ष में समय परिमाण समान है लेकिन x- अक्ष में आयाम 4 से घटकर 2 हो जाता है। इसलिए, यह समय संपीड़न का मामला है।
समय विस्तार
जब समय को निरंतर अल्फा द्वारा विभाजित किया जाता है, तो संकेत के वाई-अक्ष परिमाण को एक्स-अक्ष परिमाण रखते हुए, अल्फा बार गुणा किया जाता है। इसलिए, इसे टाइम एक्सपेंशन टाइप सिग्नल कहा जाता है।
Example
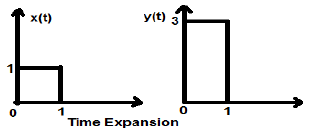
आइए हम एक वर्गाकार सिग्नल x (t) पर विचार करें, परिमाण 1. जब हम समय को लगातार 3 से घटाते हैं, जैसे कि $ x (t) \ rightarrow y (t) \ rightarrow x (\ frac {t} {3}) ) $, फिर सिग्नल के आयाम को 3 गुना संशोधित किया जाता है जो नीचे दिए गए आंकड़े में दिखाया गया है।
आयाम स्केलिंग
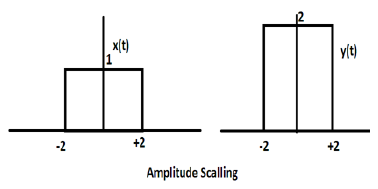
सिग्नल के आयाम के साथ एक स्थिरांक का गुणा आयाम स्केलिंग का कारण बनता है। स्थिरांक के संकेत के आधार पर, यह या तो आयाम स्केलिंग या क्षीणन हो सकता है। आइए एक वर्ग तरंग संकेत x (t) = t (t / 4) पर विचार करें।
मान लीजिए कि हम एक और फ़ंक्शन y (t) = 2 t (t / 4) परिभाषित करते हैं। इस स्थिति में, y- अक्ष का मान दोगुना हो जाएगा, समय के अक्ष का मान रखते हुए। नीचे दिए गए आंकड़े में सचित्र है।
Z (t) के रूप में परिभाषित एक और वर्ग तरंग फ़ंक्शन पर विचार करें जहां z (t) = 0.5 Consider (t / 4)। यहाँ, फ़ंक्शन z (t) का आयाम x (t) का आधा होगा अर्थात समय अक्ष शेष रहेगा, आयाम अक्ष को आधा किया जाएगा। यह नीचे दिए गए आंकड़े से दर्शाया गया है।