डीएसपी - सीटी सिग्नल का वर्गीकरण
संकेतों पर निष्पादित विभिन्न स्थितियों या संचालन के अनुसार निरंतर समय संकेतों को वर्गीकृत किया जा सकता है।
सम और विषम संकेत
यहां तक कि सिग्नल भी
एक संकेत के लिए कहा जाता है भले ही यह निम्नलिखित स्थिति को संतुष्ट करता है;
$ $ x (-t) = x (t) $ $संकेत के समय उलट यहाँ आयाम पर किसी भी परिवर्तन का मतलब नहीं है। उदाहरण के लिए, नीचे दिखाए गए त्रिकोणीय लहर पर विचार करें।
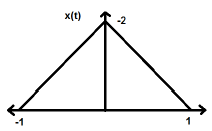
त्रिकोणीय संकेत एक भी संकेत है। चूंकि, यह Y- अक्ष के बारे में सममित है। हम कह सकते हैं कि यह Y- अक्ष के बारे में दर्पण छवि है।
नीचे दिए गए चित्र में दिखाए गए अनुसार एक और संकेत पर विचार करें।
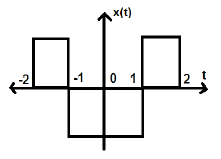
हम देख सकते हैं कि उपरोक्त संकेत सम है क्योंकि यह Y- अक्ष के बारे में सममित है।
अजीब संकेत
एक संकेत को विषम कहा जाता है, अगर यह निम्नलिखित स्थिति को संतुष्ट करता है
$ $ x (-t) = -x (t) $ $यहाँ, दोनों समय उलट और आयाम परिवर्तन एक साथ होते हैं।
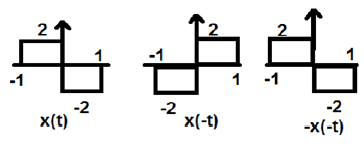
ऊपर दिए गए चित्र में, हम एक चरण सिग्नल x (t) देख सकते हैं। यह जांचने के लिए कि यह एक विषम संकेत है या नहीं, पहले हम समय उलटा करते हैं अर्थात x (-t) और परिणाम जैसा कि चित्र में दिखाया गया है। फिर हम परिणामी संकेत के आयाम (-x -t) को उल्टा करते हैं और हमें परिणाम प्राप्त होता है जैसा कि चित्र में दिखाया गया है।
यदि हम पहली और तीसरी तरंग की तुलना करते हैं, तो हम देख सकते हैं कि वे समान हैं, अर्थात x (t) = -x (-t), जो हमारे मानदंड को संतुष्ट करता है। इसलिए, उपरोक्त संकेत एक अजीब संकेत है।
सम और विषम संकेतों से संबंधित कुछ महत्वपूर्ण परिणाम नीचे दिए गए हैं।
- यहाँ तक कि × सम =
- विषम × विषम = सम
- यहां तक कि × विषम = विषम
- सम Even सम = भी
- विषम ± विषम = विषम
- सम = विषम = न भी विषम
किसी भी संकेत का सम या विषम रूप में प्रतिनिधित्व करना
कुछ संकेतों को सीधे या विषम प्रकार में वर्गीकृत नहीं किया जा सकता है। इन्हें सम और विषम संकेत दोनों के संयोजन के रूप में दर्शाया गया है।
$ $ x (t) \ rightarrow x_ {e} (t) + x_ {0} (t) $ $जहाँ x e (t) सम संकेत का प्रतिनिधित्व करता है और x o (t) विषम संकेत का प्रतिनिधित्व करता है
$$ x_ {ई} (टी) = \ frac {[x (टी) + x (-t)]} {2} $$तथा
$$ x_ {0} (टी) = \ frac {[x (टी) -x (-t)]} {2} $$उदाहरण
संकेत के सम और विषम भागों का पता लगाएं $ x (n) = t + t ^ {2} + t ^ {3} $
Solution - एक्स (एन) को उलटने से, हम प्राप्त करते हैं
$ $ x (-n) = -t + t ^ {2} -t ^ {3} $ $
अब, सूत्र के अनुसार, समान भाग
$ $ x_ {e} (t) = \ frac {x (t) + x (-t)} {2} $ $
$ $ = \ frac {[(t + t ^ {2} + t ^ {3}) + (- t + t ^ {2} -t ^ {3}]}} {2} $ $
$ $ = t ^ {2} $ $
इसी प्रकार, सूत्र के अनुसार विषम भाग है
$$ x_ {0} (टी) = \ frac {[x (टी) -x (-t)]} {2} $$
$$ = \ frac {[(t + t ^ {2} + t ^ {3}) - (- t + t ^ {2} -t ^ {3}]]} {2} $ $
$ $ = t + t ^ {3} $ $
आवधिक और गैर-आवधिक संकेत
आवधिक संकेत
आवधिक संकेत समय के कुछ अंतराल के बाद खुद को दोहराता है। हम इसे समीकरण रूप में दिखा सकते हैं -
$ $ x (t) = x (t) \ pm एनटी $ $जहां, n = एक पूर्णांक (1,2,3 ……)
टी = मौलिक समय अवधि (एफ़टीपी) ≠ 0 और time time
मौलिक समय अवधि (एफ़टीपी) समय का सबसे छोटा सकारात्मक और निश्चित मूल्य है जिसके लिए संकेत आवधिक है।
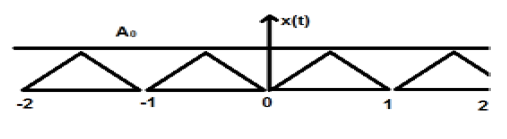
आयाम ए के ऊपर एक त्रिकोणीय संकेत दिखाया गया है। यहां, संकेत हर 1 सेकंड के बाद दोहरा रहा है। इसलिए, हम कह सकते हैं कि संकेत आवधिक है और इसका एफ़टीपी 1 सेकंड है।
गैर-आवधिक संकेत
बस, हम कह सकते हैं, संकेत, जो आवधिक नहीं हैं, प्रकृति में गैर-आवधिक हैं। स्पष्ट रूप से, ये संकेत किसी भी अंतराल समय के बाद खुद को दोहराएंगे नहीं।
गैर-आवधिक संकेत एक निश्चित प्रारूप का पालन नहीं करते हैं; इसलिए, कोई विशेष गणितीय समीकरण उनका वर्णन नहीं कर सकता है।
ऊर्जा और पावर सिग्नल
एक संकेत को एक ऊर्जा संकेत कहा जाता है, यदि और केवल अगर, निहित कुल ऊर्जा परिमित और गैर-शून्य (0 <ई <<) है। इसलिए, किसी भी ऊर्जा प्रकार के संकेत के लिए, कुल सामान्यीकृत संकेत परिमित और गैर-शून्य है।
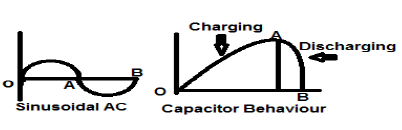
एक साइनसोइडल एसी वर्तमान संकेत ऊर्जा प्रकार संकेत का एक आदर्श उदाहरण है क्योंकि यह एक मामले में सकारात्मक आधा चक्र में है और फिर अगले आधे चक्र में नकारात्मक है। इसलिए, इसकी औसत शक्ति शून्य हो जाती है।
एक दोषरहित संधारित्र भी ऊर्जा प्रकार संकेत का एक आदर्श उदाहरण है क्योंकि जब यह स्रोत से जुड़ा होता है तो यह अपने इष्टतम स्तर तक चार्ज करता है और जब स्रोत को हटा दिया जाता है, तो यह एक लोड के माध्यम से ऊर्जा की समान मात्रा को नष्ट कर देता है और अपनी औसत शक्ति बनाता है। शून्य।
किसी भी परिमित संकेत x (t) के लिए ऊर्जा को E के रूप में चिह्नित किया जा सकता है और इसे लिखा जाता है;
$ $ E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt $ $ऊर्जा प्रकार के संकेतों का स्पेक्ट्रल घनत्व विभिन्न आवृत्ति स्तरों पर वितरित ऊर्जा की मात्रा देता है।
पावर टाइप सिग्नल
एक सिग्नल को पावर टाइप सिग्नल कहा जाता है, यदि और केवल अगर, सामान्यीकृत औसत शक्ति परिमित और गैर-शून्य है (यानी <p <<)। पावर टाइप सिग्नल के लिए, सामान्यीकृत औसत शक्ति परिमित और गैर-शून्य है। लगभग सभी आवधिक संकेत पावर सिग्नल हैं और उनकी औसत शक्ति परिमित और गैर-शून्य है।
गणितीय रूप में, एक सिग्नल x (t) की शक्ति के रूप में लिखा जा सकता है;
$ $ P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {- T / 2} ^ {+ T / 2} x ^ {2} (t) dt $ $ऊर्जा और पावर सिग्नल के बीच अंतर
निम्न तालिका ऊर्जा और पावर सिग्नल के अंतर को सारांशित करती है।
| पावर सिग्नल | ऊर्जा संकेत |
|---|---|
| व्यावहारिक आवधिक संकेत शक्ति संकेत हैं। | गैर-आवधिक संकेत ऊर्जा संकेत हैं। |
| यहां, सामान्यीकृत औसत शक्ति परिमित और गैर-शून्य है। | यहां, कुल सामान्यीकृत ऊर्जा परिमित और गैर-शून्य है। |
| गणित के अनुसार, $ $ P = \ lim_ {T \ rightarrow \ infty} 1 / T \ int _ {- T / 2} ^ {+ T / 2} x ^ {2} (t) dt $ $ |
गणित के अनुसार, $ $ E = \ int _ {- \ infty} ^ {+ \ infty} x ^ {2} (t) dt $ $ |
| इन संकेतों का अस्तित्व समय के साथ अनंत है। | ये संकेत सीमित समय के लिए मौजूद हैं। |
| पावर सिग्नल की ऊर्जा अनंत समय पर अनंत है। | ऊर्जा सिग्नल की शक्ति अनंत समय से शून्य है। |
हल के उदाहरण
Example 1 - एक सिग्नल की शक्ति का पता लगाएं $ z (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) + 4 \ sin (3 \ Pi + 30 ^ {o}) $
Solution- उपर्युक्त दो संकेत एक-दूसरे के लिए ऑर्थोगोनल हैं क्योंकि उनकी आवृत्ति की शर्तें एक-दूसरे के समान होती हैं और उनमें समान चरण अंतर भी होता है। तो, कुल शक्ति व्यक्तिगत शक्तियों का योग होगी।
$ Z (t) = x (t) + y (t) $
जहाँ $ x (t) = 2 \ cos (3 \ Pi t + 30 ^ {o}) $ और $ y (t) = 4 \ sin (3 \ Pi + 30 ^ {o}) $
$ X (t) = \ frac {2 ^ {2}} {2} = 2 $ की शक्ति
$ Y (t) = \ frac {4 ^ {2}} {2} = 8 $ की शक्ति
इसलिए, $ P (z) = p (x) + p (y) = 2 + 8 = 10 $ … Ans।
Example 2 - परीक्षण करें कि सिग्नल दिए गए $ x (t) = t ^ {2} + j \ sin t $ संयुग्म है या नहीं?
Solution- यहाँ, t 2 का वास्तविक भाग सम और विषम भाग (काल्पनिक) $ \ sin t $ विषम है। तो उपरोक्त संकेत Conjugate सिग्नल है।
Example 3 - सत्यापित करें कि क्या $ X (t) = \ sin \ omega t $ एक विषम संकेत या सम संकेत है।
Solution - दिए गए $ X (t) = \ sin \ omega t $
समय के विपरीत, हम $ \ sin (- \ omega t) $ प्राप्त करेंगे
लेकिन हम जानते हैं कि $ \ sin (- \ phi) = - \ sin \ phi $।
इसलिए,
$$ \ sin (- \ omega t) = - \ sin \ omega t $$यह सिग्नल के विषम होने की स्थिति को संतुष्ट करता है। इसलिए, $ \ sin \ omega t $ एक अजीब संकेत है।