凸最適化-最小値と最大値
極小値または最小化
$ \ bar {x} \ in \:S $は、$ f \ left(\ bar {x} \ right)\ leq f \ left(x \ right)、\の場合、関数$ f $の極小値であると言われます。 forall x \ in N_ \ varepsilon \ left(\ bar {x} \ right)$ここで、$ N_ \ varepsilon \ left(\ bar {x} \ right)$は、$ \ bar {x} $の近傍、つまり$を意味します。 N_ \ varepsilon \ left(\ bar {x} \ right)$は$ \ left \ |を意味します x- \ bar {x} \ right \ | <\ varepsilon $
ローカルマキシマまたはマキシマイザー
$ \ bar {x} \ in \:S $は、$ f \ left(\ bar {x} \ right)\ geq f \ left(x \ right)、\の場合、関数$ f $の極大値であると言われます。 forall x \ in N_ \ varepsilon \ left(\ bar {x} \ right)$ここで、$ N_ \ varepsilon \ left(\ bar {x} \ right)$は、$ \ bar {x} $の近傍、つまり$を意味します。 N_ \ varepsilon \ left(\ bar {x} \ right)$は$ \ left \ |を意味します x- \ bar {x} \ right \ | <\ varepsilon $
グローバル最小値
$ \ bar {x} \ in \:S $は、$ f \ left(\ bar {x} \ right)\ leq f \ left(x \ right)、\の場合、関数$ f $のグローバル最小値であると言われます。 forall x \ in S $
グローバル最大値
$ \ bar {x} \ in \:S $は、$ f \ left(\ bar {x} \ right)\ geq f \ left(x \ right)、\の場合、関数$ f $のグローバル最大値であると言われます。 forall x \ in S $
例
Step 1− $ f \ left(\ bar {x} \ right)= \ left |の極小値と極大値を見つけます。x ^ 2-4 \ right | $
Solution −

上記の関数のグラフから、極小値は$ x = \ pm 2 $で発生し、極大値は$ x = 0 $で発生することが明らかです。
Step 2−関数$ f \ left(x \ right)= \ left |のグローバル最小値を見つけます。4x ^ 3-3x ^ 2 + 7 \ right | $
Solution −
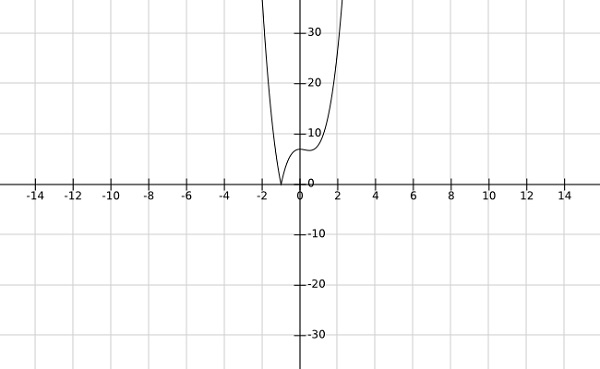
上記の関数のグラフから、グローバル最小値が$ x = -1 $で発生することが明らかです。