凸最適化-クイックガイド
このコースは、さまざまな工学および科学アプリケーションで発生する非線形最適化問題を解決したい学生に役立ちます。このコースは、線形計画法の基本理論から始まり、凸集合と関数の概念、および関連する用語を紹介して、非線形計画法の問題を解決するために必要なさまざまな定理を説明します。このコースでは、このような問題を解決するために使用されるさまざまなアルゴリズムを紹介します。この種の問題は、機械学習、電気工学の最適化問題など、さまざまなアプリケーションで発生します。生徒は高校の数学の概念と計算について事前に知っている必要があります。
このコースでは、学生は、いくつかの制約を条件として、$ min f \ left(x \ right)$のような最適化問題を解くことを学びます。
これらの問題は、関数$ f \ left(x \ right)$が線形関数であり、制約が線形である場合に簡単に解決できます。それからそれは線形計画問題(LPP)と呼ばれます。しかし、制約が非線形である場合、上記の問題を解決することは困難です。関数をグラフにプロットできない限り、最適化を分析することは1つの方法ですが、3次元を超える場合は関数をプロットできません。したがって、このような問題を解決するための非線形計画法または凸計画法の手法が登場します。これらのチュートリアルでは、そのようなテクニックの学習に焦点を当て、最後に、そのような問題を解決するためのいくつかのアルゴリズムを学びます。まず、凸計画問題の基礎となる凸集合の概念を紹介します。次に、凸関数の導入により、これらの問題を解決するためのいくつかの重要な定理と、これらの定理に基づくいくつかのアルゴリズムについて説明します。
用語
スペース$ \ mathbb {R} ^ n $-これは実数のn次元ベクトルであり、次のように定義されます-$ \ mathbb {R} ^ n = \ left \ {\ left(x_1、x_2、.. .. 、x_n \ right)^ {\ tau}:x_1、x_2、....、x_n \ in \ mathbb {R} \ right \} $
スペース$ \ mathbb {R} ^ {mXn} $ −これは、$ mXn $次のすべての実数値行列のセットです。
方法論
線形最適化とも呼ばれる線形計画法は、関係が本質的に線形である数学的問題を解決するために使用される手法です。線形計画法の基本的な性質は、最大化または最小化することですobjective function いくつかの対象と constraints。目的関数は、問題の数学モデルから得られる線形関数です。制約は、モデルに課せられる条件であり、線形でもあります。
- 与えられた質問から、目的関数を見つけます。
- 制約を見つけます。
- グラフに制約を描画します。
- すべての制約の交点によって形成される実行可能領域を見つけます。
- 実行可能領域の頂点を見つけます。
- これらの頂点で目的関数の値を見つけます。
- (質問に応じて)目的関数を最大化または最小化する頂点が答えです。
例
Step 1 − $ 5x + 3y $を最大化する
$ x + y \ leq 2 $、
$ 3x + y \ leq 3 $、
$ x \ geq 0 \:および\:y \ geq 0 $
Solution −
最初のステップは、グラフ上で実行可能領域を見つけることです。

グラフから明らかなように、実行可能領域の頂点は次のとおりです。
$ \ left(0、0 \ right)\ left(0、2 \ right)\ left(1、0 \ right)\ left(\ frac {1} {2}、\ frac {3} {2} \ right )$
$ f \ left(x、y \ right)= 5x + 3y $とします
これらの値を目的関数に入れると、次のようになります。
$ f \ left(0、0 \ right)$ = 0
$ f \ left(0、2 \ right)$ = 6
$ f \ left(1、0 \ right)$ = 5
$ f \ left(\ frac {1} {2}、\ frac {3} {2} \ right)$ = 7
したがって、関数は$ \ left(\ frac {1} {2}、\ frac {3} {2} \ right)$で最大になります。
Step 2−時計会社はデジタル時計と機械式時計を製造しています。長期的な予測では、毎日少なくとも100個のデジタル時計と80個の機械式時計の需要が見込まれています。生産能力に限りがあるため、1日200本のデジタル時計と170本の機械式時計しか製造できません。配送契約を満たすために、毎日合計200個以上の時計が発送されます。
販売された各デジタル時計が$ \ $ 2 $の損失をもたらすが、各機械式時計が$ \ $ 5 $の利益を生み出す場合、純利益を最大化するために、各タイプを1日にいくつ作成する必要がありますか?
Solution −
$ x $を製造されたデジタル時計の数とします
$ y $は生産された機械式時計の数です
質問によると、毎日少なくとも100個のデジタル時計を製造し、最大200個のデジタル時計を製造することができます。
$ \ Rightarrow 100 \ leq \:x \ leq 200 $
同様に、少なくとも80個の機械式時計を毎日製造し、最大170個の機械式時計を製造することができます。
$ \ Rightarrow 80 \ leq \:y \ leq 170 $
毎日少なくとも200個の時計が生産されるためです。
$ \ Rightarrow x + y \ leq 200 $
販売された各デジタル時計は$ \ $ 2 $の損失をもたらしますが、各機械式時計は$ \ $ 5 $の利益を生み出します。
総利益は次のように計算できます
$利益= -2x + 5y $
そして、利益を最大化する必要があります。したがって、質問は次のように定式化できます。
$ -2x + 5y $を最大化する
$ 100 \:\ leq x \:\ leq 200 $
$ 80 \:\ leq y \:\ leq 170 $
$ x + y \:\ leq 200 $
上記の方程式をグラフにプロットすると、次のようになります。

実行可能領域の頂点は次のとおりです。
$ \ left(100、170 \ right)\ left(200、170 \ right)\ left(200、180 \ right)\ left(120、80 \ right)および\ left(100、100 \ right)$
目的関数の最大値は$ \ left(100、170 \ right)$で得られます。したがって、純利益を最大化するには、100台のデジタル時計と170台の機械式時計を製造する必要があります。
ノルムは、ベクトルまたは変数に厳密に正の値を与える関数です。
Normは関数$ f:\ mathbb {R} ^ n \ rightarrow \ mathbb {R} $
規範の基本的な特徴は次のとおりです。
$ X $を$ X \ in \ mathbb {R} ^ n $のようなベクトルとします。
$ \左\ | x \ right \ | \ geq 0 $
$ \左\ | x \ right \ | = 0 \ Leftrightarrow x = 0 \ forall x \ in X $
$ \ left \ | \ alpha x \ right \ | = \ left | \ alpha \ right | \ left \ | x \ right \ | \ forall \:x \ in Xおよび\:\ alpha \:is \:a \:scalar $
$ \左\ | x + y \ right \ | \ leq \ left \ | x \ right \ | + \ left \ | y \ right \ | \ forall x、y \ in X $
$ \左\ | xy \ right \ | \ geq \ left \ | \左\ | x \ right \ |-\ left \ | y \ right \ | \ right \ | $
定義により、ノルムは次のように計算されます-
$ \左\ | x \ right \ | _1 = \ displaystyle \ sum \ limits_ {i = 1} ^ n \ left | x_i \ right | $
$ \左\ | x \ right \ | _2 = \ left(\ displaystyle \ sum \ limits_ {i = 1} ^ n \ left | x_i \ right | ^ 2 \ right)^ {\ frac {1} {2}} $
$ \左\ | x \ right \ | _p = \ left(\ displaystyle \ sum \ limits_ {i = 1} ^ n \ left | x_i \ right | ^ p \ right)^ {\ frac {1} {p}}、1 \ leq p \ leq \ infty $
ノルムは連続関数です。
証明
定義上、$ X \ Rightarrow f \ left(x_n \ right)\ rightarrow f \ left(x \ right)$の$ x_n \ rightarrow x $の場合、$ f \ left(x \ right)$は定数関数です。
$ f \ left(x \ right)= \ left \ |とします。x \ right \ | $
したがって、$ \ left | f \ left(x_n \ right)-f \ left(x \ right)\ right | = \ left | \左\ | x_n \ right \ | -\左\ | x \ right \ | \ right | \ leq \ left | \左| x_n-x \ right | \:\ right | $
$ x_n \ rightarrow x $なので、$ \ left \ | x_n-x \ right \ | \ rightarrow 0 $
したがって、$ \ left | f \ left(x_n \ right)-f \ left(x \ right)\ right | \ leq 0 \ Rightarrow \ left | f \ left(x_n \ right)-f \ left(x \ right)\ right | = 0 \ Rightarrow f \ left(x_n \ right)\ rightarrow f \ left(x \ right)$
したがって、ノルムは連続関数です。
内積は、ベクトルのペアにスカラーを与える関数です。
内積-$ f:\ mathbb {R} ^ n \ times \ mathbb {R} ^ n \ rightarrow \ kappa $ここで、$ \ kappa $はスカラーです。
内積の基本的な特徴は次のとおりです-
$ X \ in \ mathbb {R} ^ n $とします
$ \ left \ langle x、x \ right \ rangle \ geq 0、\ forall x \ in X $
$ \ left \ langle x、x \ right \ rangle = 0 \ Leftrightarrow x = 0、\ forall x \ in X $
$ \ left \ langle \ alpha x、y \ right \ rangle = \ alpha \ left \ langle x、y \ right \ rangle、\ forall \ alpha \ in \ kappa \:and \:\ forall x、y \ in X $
$ \ left \ langle x + y、z \ right \ rangle = \ left \ langle x、z \ right \ rangle + \ left \ langle y、z \ right \ rangle、\ forall x、y、z \ in X $
$ \ left \ langle \ overline {y、x} \ right \ rangle = \ left(x、y \ right)、\ forall x、y \ in X $
Note −
ノルムと内積の関係:$ \ left \ | x \ right \ | = \ sqrt {\ left(x、x \ right)} $
$ \ forall x、y \ in \ mathbb {R} ^ n、\ left \ langle x、y \ right \ rangle = x_1y_1 + x_2y_2 + ... + x_ny_n $
例
1. $ x = \ left(1,2,1 \ right)\:と\:y = \ left(3、-1,3 \ right)$の内積を見つけます
解決
$ \ left \ langle x、y \ right \ rangle = x_1y_1 + x_2y_2 + x_3y_3 $
$ \ left \ langle x、y \ right \ rangle = \ left(1 \ times3 \ right)+ \ left(2 \ times-1 \ right)+ \ left(1 \ times3 \ right)$
$ \ left \ langle x、y \ right \ rangle = 3 + \ left(-2 \ right)+3 $
$ \ left \ langle x、y \ right \ rangle = 4 $
2. $ x = \ left(4,9,1 \ right)、y = \ left(-3,5,1 \ right)$および$ z = \ left(2,4,1 \ right)$の場合、 $ \ left(x + y、z \ right)$を見つけます
解決
ご存知のように、$ \ left \ langle x + y、z \ right \ rangle = \ left \ langle x、z \ right \ rangle + \ left \ langle y、z \ right \ rangle $
$ \ left \ langle x + y、z \ right \ rangle = \ left(x_1z_1 + x_2z_2 + x_3z_3 \ right)+ \ left(y_1z_1 + y_2z_2 + y_3z_3 \ right)$
$ \ left \ langle x + y、z \ right \ rangle = \ left \ {\ left(4 \ times 2 \ right)+ \ left(9 \ times 4 \ right)+ \ left(1 \ times1 \ right) \ right \} + $
$ \ left \ {\ left(-3 \ times2 \ right)+ \ left(5 \ times4 \ right)+ \ left(1 \ times 1 \ right)\ right \} $
$ \ left \ langle x + y、z \ right \ rangle = \ left(8 + 36 + 1 \ right)+ \ left(-6 + 20 + 1 \ right)$
$ \ left \ langle x + y、z \ right \ rangle = 45 + 15 $
$ \ left \ langle x + y、z \ right \ rangle = 60 $
極小値または最小化
$ \ bar {x} \ in \:S $は、$ f \ left(\ bar {x} \ right)\ leq f \ left(x \ right)、\の場合、関数$ f $の極小値であると言われます。 forall x \ in N_ \ varepsilon \ left(\ bar {x} \ right)$ここで、$ N_ \ varepsilon \ left(\ bar {x} \ right)$は、$ \ bar {x} $の近傍、つまり$を意味します。 N_ \ varepsilon \ left(\ bar {x} \ right)$は$ \ left \ |を意味します x- \ bar {x} \ right \ | <\ varepsilon $
ローカルマキシマまたはマキシマイザー
$ \ bar {x} \ in \:S $は、$ f \ left(\ bar {x} \ right)\ geq f \ left(x \ right)、\の場合、関数$ f $の極大値であると言われます。 forall x \ in N_ \ varepsilon \ left(\ bar {x} \ right)$ここで、$ N_ \ varepsilon \ left(\ bar {x} \ right)$は、$ \ bar {x} $の近傍、つまり$を意味します。 N_ \ varepsilon \ left(\ bar {x} \ right)$は$ \ left \ |を意味します x- \ bar {x} \ right \ | <\ varepsilon $
グローバル最小値
$ \ bar {x} \ in \:S $は、$ f \ left(\ bar {x} \ right)\ leq f \ left(x \ right)、\の場合、関数$ f $のグローバル最小値であると言われます。 forall x \ in S $
グローバル最大値
$ \ bar {x} \ in \:S $は、$ f \ left(\ bar {x} \ right)\ geq f \ left(x \ right)、\の場合、関数$ f $のグローバル最大値であると言われます。 forall x \ in S $
例
Step 1− $ f \ left(\ bar {x} \ right)= \ left |の極小値と極大値を見つけます。x ^ 2-4 \ right | $
Solution −

上記の関数のグラフから、極小値は$ x = \ pm 2 $で発生し、極大値は$ x = 0 $で発生することが明らかです。
Step 2−関数$ f \ left(x \ right)= \ left |のグローバル最小値を見つけます。4x ^ 3-3x ^ 2 + 7 \ right | $
Solution −
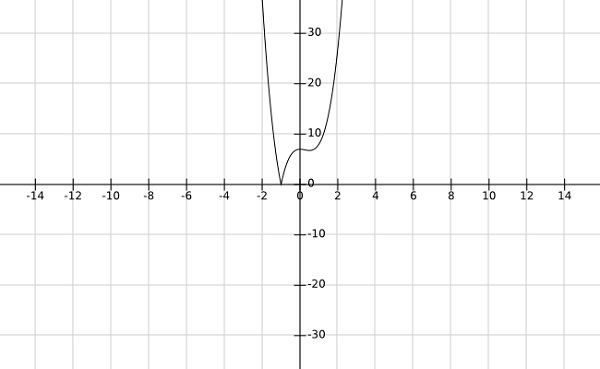
上記の関数のグラフから、グローバル最小値が$ x = -1 $で発生することが明らかです。
$ S \ subseteq \ mathbb {R} ^ n $とします。集合Sの任意の2点を結ぶ線分もSに属する場合、つまり$ x_1、x_2 \ in S $の場合、集合Sは凸であると言われます。 、次に$ \ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ in S $ここで、$ \ lambda \ in \ left(0,1 \ right)$。
Note −
- 2つの凸集合の和集合は、凸である場合とそうでない場合があります。
- 2つの凸集合の交点は常に凸です。
Proof
$ S_1 $と$ S_2 $を2つの凸集合とします。
$ S_3 = S_1 \ cap S_2 $とします
$ x_1、x_2 \ in S_3 $とします
$ S_3 = S_1 \ cap S_2 $なので、$ x_1、x_2 \ in S_1 $と$ x_1、x_2 \ in S_2 $
$ S_i $は凸集合なので、$ \ forall $ $ i \ in 1,2、$
したがって、$ \ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ in S_i $ここで、$ \ lambda \ in \ left(0,1 \ right)$
したがって、$ \ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ in S_1 \ cap S_2 $
$ \ Rightarrow \ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ in S_3 $
したがって、$ S_3 $は凸集合です。
$ \ displaystyle \ sum \ limits_ {i = 1} ^ k \ lambda_ix_i $の形式の加重平均。ここで、$ \ displaystyle \ sum \ limits_ {i = 1} ^ k \ lambda_i = 1 $および$ \ lambda_i \ geq 0 、\ forall i \ in \ left [1、k \ right] $は、$ x_1、x_2、.... x_k。$の円錐曲線の組み合わせと呼ばれます。
$ \ displaystyle \ sum \ limits_ {i = 1} ^ k \ lambda_ix_i $の形式の加重平均。ここで、$ \ displaystyle \ sum \ limits_ {i = 1} ^ k \ lambda_i = 1 $は、$ x_1のアフィン結合と呼ばれます。 、x_2、.... x_k。$
$ \ displaystyle \ sum \ limits_ {i = 1} ^ k \ lambda_ix_i $の形式の加重平均は、$ x_1、x_2、.... x_k。$の線形結合と呼ばれます。
例
Step 1 −集合$ S = \ left \ {x \ in \ mathbb {R} ^ n:Cx \ leq \ alpha \ right \} $が凸集合であることを証明します。
解決
$ x_1 $と$ x_2 \ in S $とします
$ \ Rightarrow Cx_1 \ leq \ alpha $および$ \:and \:Cx_2 \ leq \ alpha $
表示するには:$ \:\:y = \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)\ in S \:\ forall \:\ lambda \ in \ left(0,1 \右)$
$ Cy = C \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)= \ lambda Cx_1 + \ left(1- \ lambda \ right)Cx_2 $
$ \ Rightarrow Cy \ leq \ lambda \ alpha + \ left(1- \ lambda \ right)\ alpha $
$ \ Rightarrow Cy \ leq \ alpha $
$ \ Rightarrow y \ in S $
したがって、$ S $は凸集合です。
Step 2 −集合$ S = \ left \ {\ left(x_1、x_2 \ right)\ in \ mathbb {R} ^ 2:x_ {1} ^ {2} \ leq 8x_2 \ right \} $が凸であることを証明するセットする。
解決
$ x、y \ in S $
$ x = \ left(x_1、x_2 \ right)$および$ y = \ left(y_1、y_2 \ right)$とします。
$ \ Rightarrow x_ {1} ^ {2} \ leq 8x_2 $および$ y_ {1} ^ {2} \ leq 8y_2 $
表示するには-$ \ lambda x + \ left(1- \ lambda \ right)y \ in S \ Rightarrow \ lambda \ left(x_1、x_2 \ right)+ \ left(1- \ lambda \ right)\ left(y_1、 y_2 \ right)\ in S \ Rightarrow \ left [\ lambda x_1 + \ left(1- \ lambda)y_2] \ in S \ right)\ right] $
$ Now、\ left [\ lambda x_1 + \ left(1- \ lambda \ right)y_1 \ right] ^ {2} = \ lambda ^ 2x_ {1} ^ {2} + \ left(1- \ lambda \ right) ^ 2y_ {1} ^ {2} +2 \ lambda \ left(1- \ lambda \ right)x_1y_1 $
しかし、$ 2x_1y_1 \ leq x_ {1} ^ {2} + y_ {1} ^ {2} $
したがって、
$ \ left [\ lambda x_1 + \ left(1- \ lambda \ right)y_1 \ right] ^ {2} \ leq \ lambda ^ 2x_ {1} ^ {2} + \ left(1- \ lambda \ right) ^ 2y_ {1} ^ {2} +2 \ lambda \ left(1- \ lambda \ right)\ left(x_ {1} ^ {2} + y_ {1} ^ {2} \ right)$
$ \ Rightarrow \ left [\ lambda x_1 + \ left(1- \ lambda \ right)y_1 \ right] ^ {2} \ leq \ lambda x_ {1} ^ {2} + \ left(1- \ lambda \ right) y_ {1} ^ {2} $
$ \ Rightarrow \ left [\ lambda x_1 + \ left(1- \ lambda \ right)y_1 \ right] ^ {2} \ leq 8 \ lambda x_2 + 8 \ left(1- \ lambda \ right)y_2 $
$ \ Rightarrow \ left [\ lambda x_1 + \ left(1- \ lambda \ right)y_1 \ right] ^ {2} \ leq 8 \ left [\ lambda x_2 + \ left(1- \ lambda \ right)y_2 \ right] $
$ \ Rightarrow \ lambda x + \ left(1- \ lambda \ right)y \ in S $
Step 3 −各整数kについて、$ S $の任意のk点のすべての凸結合が$ S $にある場合に限り、集合$ S \ in \ mathbb {R} ^ n $が凸であることを示します。
解決
$ S $を凸集合とします。次に、表示します。
$ c_1x_1 + c_2x_2 + ..... + c_kx_k \ in S、\ displaystyle \ sum \ limits_ {1} ^ k c_i = 1、c_i \ geq 0、\ forall i \ in 1,2、....、k $
帰納法による証明
$ k = 1、x_1 \ in Sの場合、c_1 = 1 \ Rightarrow c_1x_1 \ in S $
$ k = 2、x_1、x_2 \ in Sの場合、c_1 + c_2 = 1 $であり、Sは凸集合であるため
$ \ Rightarrow c_1x_1 + c_2x_2 \ in S. $
Sのm点の凸結合がSにあるとします。
$ c_1x_1 + c_2x_2 + ... + c_mx_m \ in S、\ displaystyle \ sum \ limits_ {1} ^ m c_i = 1、c_i \ geq 0、\ forall i \ in 1,2、...、m $
ここで、$ x_1、x_2 ....、x_m、x_ {m + 1} \ in S $とします。
$ x = \ mu_1x_1 + \ mu_2x_2 + ... + \ mu_mx_m + \ mu_ {m + 1} x_ {m + 1} $とします
$ x = \ left(\ mu_1 + \ mu_2 + ... + \ mu_m \ right)\ frac {\ mu_1x_1 + \ mu_2x_2 + \ mu_mx_m} {\ mu_1 + \ mu_2 + ......... + \ mu_m} + \ mu_ {m + 1} x_ {m + 1} $
$ y = \ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_mx_m} {\ mu_1 + \ mu_2 + ......... + \ mu_m} $とします
$ \ Rightarrow x = \ left(\ mu_1 + \ mu_2 + ... + \ mu_m \ right)y + \ mu_ {m + 1} x_ {m + 1} $
係数の合計が1であるため、$ y \ in S $になります。
$ \ Rightarrow x \ in S $ Sは凸集合であり、$ y、x_ {m + 1} \ in S $
したがって、誘導によって証明された。
集合$ A $は、任意の2つの異なる点について、これらの点を通る線が集合$ A $にある場合、アフィン集合であると言われます。
Note −
$ S $は、ポイントのすべてのアフィン結合が含まれている場合にのみ、アフィンセットです。
空のセットと単集合は、両方ともアフィンセットと凸セットです。
たとえば、線形方程式の解はアフィン集合です。
証明
Sを線形方程式の解とします。
定義上、$ S = \ left \ {x \ in \ mathbb {R} ^ n:Ax = b \ right \} $
$ x_1、x_2 \ in S \ Rightarrow Ax_1 = b $および$ Ax_2 = b $とします。
証明するには:$ A \ left [\ theta x_1 + \ left(1- \ theta \ right)x_2 \ right] = b、\ forall \ theta \ in \ left(0,1 \ right)$
$ A \ left [\ theta x_1 + \ left(1- \ theta \ right)x_2 \ right] = \ theta Ax_1 + \ left(1- \ theta \ right)Ax_2 = \ theta b + \ left(1- \ theta \ right )b = b $
したがって、Sはアフィン集合です。
定理
$ C $がアフィンセットで$ x_0 \ in C $の場合、セット$ V = C-x_0 = \ left \ {x-x_0:x \ in C \ right \} $はCの部分空間です。
証明
$ x_1、x_2 \ in V $とします
表示するには:$ \ alpha x_1 + \ beta x_2 \ in V $ for some $ \ alpha、\ beta $
ここで、Vの定義により、$ x_1 + x_0 \ in C $および$ x_2 + x_0 \ in C $
ここで、$ \ alpha x_1 + \ beta x_2 + x_0 = \ alpha \ left(x_1 + x_0 \ right)+ \ beta \ left(x_2 + x_0 \ right)+ \ left(1- \ alpha- \ beta \ right)x_0 $
ただし、Cはアフィンセットであるため、$ \ alpha \ left(x_1 + x_0 \ right)+ \ beta \ left(x_2 + x_0 \ right)+ \ left(1- \ alpha- \ beta \ right)x_0 \ in C $ 。
したがって、$ \ alpha x_1 + \ beta x_2 \ in V $
したがって、証明されました。
Sの点のセットの凸包は、その内部または境界上のSのすべての点を含む最小の凸領域の境界です。
または
$ S \ subseteq \ mathbb {R} ^ n $とします。$ Co \ left(S \ right)$で表されるSの凸包は、Sのすべての凸結合の集合です。つまり、$ x \ in Co \ left (S \ right)$ $ x \ in \ displaystyle \ sum \ limits_ {i = 1} ^ n \ lambda_ix_i $の場合に限り、$ \ displaystyle \ sum \ limits_ {1} ^ n \ lambda_i = 1 $および$ \ lambda_i \ geq 0 \ forall x_i \ in S $
Remark −平面内のSの点のセットの凸面は凸多角形を定義し、多角形の境界上のSの点は多角形の頂点を定義します。
Theorem $ Co \ left(S \ right)= \ left \ {x:x = \ displaystyle \ sum \ limits_ {i = 1} ^ n \ lambda_ix_i、x_i \ in S、\ displaystyle \ sum \ limits_ {i = 1} ^ n \ lambda_i = 1、\ lambda_i \ geq 0 \ right \} $凸包が凸集合であることを示します。
証明
$ x_1、x_2 \ in Co \ left(S \ right)$とし、次に$ x_1 = \ displaystyle \ sum \ limits_ {i = 1} ^ n \ lambda_ix_i $および$ x_2 = \ displaystyle \ sum \ limits_ {i = 1} ^ n \ lambda_ \ gamma x_i $ここで、$ \ displaystyle \ sum \ limits_ {i = 1} ^ n \ lambda_i = 1、\ lambda_i \ geq 0 $、$ \ displaystyle \ sum \ limits_ {i = 1} ^ n \ gamma_i = 1、\ gamma_i \ geq0 $
$ \ theta \ in \ left(0,1 \ right)、\ theta x_1 + \ left(1- \ theta \ right)x_2 = \ theta \ displaystyle \ sum \ limits_ {i = 1} ^ n \ lambda_ix_i + \ leftの場合(1- \ theta \ right)\ displaystyle \ sum \ limits_ {i = 1} ^ n \ gamma_ix_i $
$ \ theta x_1 + \ left(1- \ theta \ right)x_2 = \ displaystyle \ sum \ limits_ {i = 1} ^ n \ lambda_i \ theta x_i + \ displaystyle \ sum \ limits_ {i = 1} ^ n \ gamma_i \左(1- \ theta \ right)x_i $
$ \ theta x_1 + \ left(1- \ theta \ right)x_2 = \ displaystyle \ sum \ limits_ {i = 1} ^ n \ left [\ lambda_i \ theta + \ gamma_i \ left(1- \ theta \ right)\右] x_i $
係数を考慮すると、
$ \ displaystyle \ sum \ limits_ {i = 1} ^ n \ left [\ lambda_i \ theta + \ gamma_i \ left(1- \ theta \ right)\ right] = \ theta \ displaystyle \ sum \ limits_ {i = 1 } ^ n \ lambda_i + \ left(1- \ theta \ right)\ displaystyle \ sum \ limits_ {i = 1} ^ n \ gamma_i = \ theta + \ left(1- \ theta \ right)= 1 $
したがって、$ \ theta x_1 + \ left(1- \ theta \ right)x_2 \ in Co \ left(S \ right)$
したがって、凸包は凸集合です。
Sを$ \ mathbb {R} ^ n $の任意のセットとします。$ x \ in Co \ left(S \ right)$の場合、$ x \ in Co \ left(x_1、x_2、....、 x_n、x_ {n + 1} \ right)$。
証明
$ x \ in Co \ left(S \ right)$なので、$ x $は、S内の有限数の点の凸結合で表されます。
$ x = \ displaystyle \ sum \ limits_ {j = 1} ^ k \ lambda_jx_j、\ displaystyle \ sum \ limits_ {j = 1} ^ k \ lambda_j = 1、\ lambda_j \ geq 0 $および$ x_j \ in S、 \ forall j \ in \ left(1、k \ right)$
$ k \ leq n + 1 $の場合、得られる結果は明らかに真です。
$ k \ geq n + 1 $の場合、$ \ left(x_2-x_1 \ right)\ left(x_3-x_1 \ right)、.....、\ left(x_k-x_1 \ right)$は線形従属です。
$ \ Rightarrow \ exists \ mu _j \ in \ mathbb {R}、2 \ leq j \ leq k $(すべてゼロではない)$ \ displaystyle \ sum \ limits_ {j = 2} ^ k \ mu _j \ left (x_j-x_1 \ right)= 0 $
$ \ mu_1 =-\ displaystyle \ sum \ limits_ {j = 2} ^ k \ mu _j $を定義してから、$ \ displaystyle \ sum \ limits_ {j = 1} ^ k \ mu_j x_j = 0、\ displaystyle \ sum \制限_ {j = 1} ^ k \ mu_j = 0 $
ここで、すべての$ \ mu_jの$がゼロに等しいわけではありません。$ \ displaystyle \ sum \ limits_ {j = 1} ^ k \ mu_j = 0 $なので、$ \ mu_j> 0,1 \ leq j \ leq k $の少なくとも1つ
次に、$ x = \ displaystyle \ sum \ limits_ {1} ^ k \ lambda_j x_j + 0 $
$ x = \ displaystyle \ sum \ limits_ {1} ^ k \ lambda_j x_j- \ alpha \ displaystyle \ sum \ limits_ {1} ^ k \ mu_j x_j $
$ x = \ displaystyle \ sum \ limits_ {1} ^ k \ left(\ lambda_j- \ alpha \ mu_j \ right)x_j $
$ \ alpha = min \ left \ {\ frac {\ lambda_j} {\ mu_j}、\ mu_j \ geq 0 \ right \} = \ frac {\ lambda_j} {\ mu _j}、$となるように$ \ alpha $を選択しますいくつかの$ i = 1,2、...、k $の場合
$ \ mu_j \ leq 0の場合、\ lambda_j- \ alpha \ mu_j \ geq 0 $
$ \ mu_j> 0の場合、\:\ frac {\ lambda _j} {\ mu_j} \ geq \ frac {\ lambda_i} {\ mu _i} = \ alpha \ Rightarrow \ lambda_j- \ alpha \ mu_j \ geq 0、 j = 1,2、... k $
特に、$ \ alpha $の定義により、$ \ lambda_i- \ alpha \ mu_i = 0 $
$ x = \ displaystyle \ sum \ limits_ {j = 1} ^ k \ left(\ lambda_j- \ alpha \ mu_j \ right)x_j $、ここで
$ \ lambda_j- \ alpha \ mu_j \ geq0 $および$ \ displaystyle \ sum \ limits_ {j = 1} ^ k \ left(\ lambda_j- \ alpha \ mu_j \ right)= 1 $および$ \ lambda_i- \ alpha \ mu_i = 0 $
したがって、xは、最大(k-1)個の点の凸結合として表すことができます。
この縮小プロセスは、xが(n + 1)要素の凸結合として表されるまで繰り返すことができます。
Sを$ \ mathbb {R} ^ n $の空でない、閉じた有界集合(コンパクト集合とも呼ばれる)とし、$ f:S \ rightarrow \ mathbb {R} $をSの連続関数とし、次に問題min $ \ left \ {f \ left(x \ right):x \ in S \ right \} $が最小値に達します。
証明
Sは空ではなく有界であるため、下限が存在します。
$ \ alpha = Inf \ left \ {f \ left(x \ right):x \ in S \ right \} $
ここで、$ S_j = \ left \ {x \ in S:\ alpha \ leq f \ left(x \ right)\ leq \ alpha + \ delta ^ j \ right \} \ forall j = 1,2、.. $および$ \ delta \ in \ left(0,1 \ right)$
infimiumの定義により、$ S_j $は、$ j $ごとに空ではありません。
$ x_j \ in S_j $を選択して、$ j = 1,2、... $のシーケンス$ \ left \ {x_j \ right \} $を取得します。
Sが有界であるため、シーケンスも有界であり、$ \ hat {x} $に収束する収束サブシーケンス$ \ left \ {y_j \ right \} $があります。したがって、$ \ hat {x} $は限界点であり、Sは閉じているため、$ \ hat {x} \ in S $です。fは連続であるため、$ f \ left(y_i \ right)\ rightarrow f \ left(\ hat {x} \ right)$。
$ \ alpha \ leq f \ left(y_i \ right)\ leq \ alpha + \ delta ^ kなので、\ alpha = \ displaystyle \ lim_ {k \ rightarrow \ infty} f \ left(y_i \ right)= f \ left( \ hat {x} \ right)$
したがって、$ \ hat {x} $が最小化ソリューションです。
備考
ワイエルシュトラスの定理が成り立つための2つの重要な必要条件があります。これらは次のとおりです-
Step 1 −集合Sは有界集合でなければなりません。
関数f \ left(x \ right)= x $について考えてみます。
これは無制限のセットであり、ドメイン内の任意の時点で最小値があります。
したがって、最小値を取得するには、Sを有界にする必要があります。
Step 2 −セットSを閉じる必要があります。
ドメイン\ left(0,1 \ right)の関数$ f \ left(x \ right)= \ frac {1} {x} $について考えてみます。
この関数は指定されたドメインで閉じられておらず、その最小値も存在しません。
したがって、最小値を取得するには、Sを閉じる必要があります。
Sを$ \ mathbb {R} ^ n $の空でない閉じた凸集合とし、$ y \ notin S $とし、$ \ exists $点$ \ bar {x} \ in S $からの最小距離y、つまり$ \ left \ | y- \ bar {x} \ right \ | \ leq \ left \ | yx \ right \ | \ forall x \ in S. $
さらに、$ \ bar {x} $は、$ \ left(y- \ hat {x} \ right)^ {T} \ left(x- \ hat {x} \ right)\ leqの場合に限り、最小化ポイントです。 0 $または$ \ left(y- \ hat {x}、x- \ hat {x} \ right)\ leq 0 $
証明
最も近い点の存在
$ S \ ne \ phi、\ exists $なので、S $のポイント$ \ hat {x} \は、yからのSの最小距離が$ \ left \ |以下になるようにします。y- \ hat {x} \ right \ | $。
$ \ hat {S} = S \ cap \ left \ {x:\ left \ |を定義します yx \ right \ | \ leq \ left \ | y- \ hat {x} \ right \ | \ right \} $
$ \ hat {S} $は閉じて有界であり、ノルムは連続関数であるため、ワイエルシュトラスの定理により、$ \ left \ |となるような最小点$ \ hat {x} \ in S $が存在します。y- \ hat {x} \ right \ | = Inf \ left \ {\ left \ | yx \ right \ |、x \ in S \ right \} $
独自性
$ \ bar {x} \ in S $が$ \ left \ |であると仮定します。y- \ hat {x} \ right \ | = \ left \ | y- \ hat {x} \ right \ | = \ alpha $
Sは凸であるため、$ \ frac {\ hat {x} + \ bar {x}} {2} \ in S $
しかし、$ \ left \ | y- \ frac {\ hat {x}-\ bar {x}} {2} \ right \ | \ leq \ frac {1} {2} \ left \ | y- \ hat {x} \ right \ | + \ frac {1} {2} \ left \ | y- \ bar {x} \ right \ | = \ alpha $
$ \ hat {x} $はyに最も近いため、厳密な不等式にすることはできません。
したがって、$ \ left \ | y- \ hat {x} \ right \ | = \ mu \ left \ | y- \ hat {x} \ right \ | $、$ \ mu $の場合
今$ \ left \ | \ mu \ right \ | = 1. $ $ \ mu = -1 $の場合、$ \ left(y- \ hat {x} \ right)=-\ left(y- \ hat {x} \ right)\右矢印y = \ frac {\ hat {x} + \ bar {x}} {2} \ in S $
しかし、$ y \ in S $。したがって、矛盾。したがって、$ \ mu = 1 \ Rightarrow \ hat {x} = \ bar {x} $
したがって、最小化ポイントは一意です。
証明の2番目の部分では、すべての$ x \に対して$ \ left(y- \ hat {x} \ right)^ {\ tau} \ left(x- \ bar {x} \ right)\ leq 0 $と仮定します。 S $で
さて、
$ \左\ | yx \ right \ | ^ {2} = \ left \ | y- \ hat {x} + \ hat {x} -x \ right \ | ^ {2} = \ left \ | y- \ hat {x} \ right \ | ^ {2} + \ left \ | \ hat {x} -x \ right \ | ^ {2} + 2 \ left(\ hat {x} -x \ right) ^ {\ tau} \ left(y- \ hat {x} \ right)$
$ \ Rightarrow \ left \ | yx \ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ right \ | ^ {2} $なぜなら$ \ left \ | \ hat {x} -x \ right \ | ^ {2} \ geq 0 $および$ \ left(\ hat {x} -x \ right)^ {T} \ left(y- \ hat {x} \ right )\ geq 0 $
したがって、$ \ hat {x} $はポイントを最小化しています。
逆に、$ \ hat {x} $が最小化ポイントであると仮定します。
$ \ Rightarrow \ left \ | yx \ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ right \ | ^ 2 \ forall x \ in S $
Sは凸集合なので。
$ \ Rightarrow \ lambda x + \ left(1- \ lambda \ right)\ hat {x} = \ hat {x} + \ lambda \ left(x- \ hat {x} \ right)\ in S $ for $ x \ in S $および$ \ lambda \ in \ left(0,1 \ right)$
さて、$ \ left \ | y- \ hat {x}-\ lambda \ left(x- \ hat {x} \ right)\ right \ | ^ {2} \ geq \ left \ | y- \ hat {x} \ right \ | ^ 2 $
そして
$ \左\ | y- \ hat {x}-\ lambda \ left(x- \ hat {x} \ right)\ right \ | ^ {2} = \ left \ | y- \ hat {x} \ right \ | ^ {2} + \ lambda ^ 2 \ left \ | x- \ hat {x} \ right \ | ^ {2} -2 \ lambda \ left(y- \ hat {x} \ right)^ {T} \ left(x- \ hat {x} \ right)$
$ \ Rightarrow \ left \ | y- \ hat {x} \ right \ | ^ {2} + \ lambda ^ {2} \ left \ | x- \ hat {x} \ right \ | -2 \ lambda \ left(y- \ hat {x} \ right)^ {T} \ left(x- \ hat {x} \ right)\ geq \ left \ | y- \ hat {x} \ right \ | ^ {2} $
$ \ Rightarrow 2 \ lambda \ left(y- \ hat {x} \ right)^ {T} \ left(x- \ hat {x} \ right)\ leq \ lambda ^ 2 \ left \ | x- \ hat {x} \ right \ | ^ 2 $
$ \ Rightarrow \ left(y- \ hat {x} \ right)^ {T} \ left(x- \ hat {x} \ right)\ leq 0 $
したがって、証明されました。
Sを$ \ mathbb {R} ^ n $と$ y \ notin S $の空でない閉じた凸集合とします。次に、各$ x \ in S $に対して$ p ^ T y> \ beta $および$ p ^ T x <\ beta $となるような非ゼロベクトル$ p $およびスカラー$ \ beta $が存在します。
証明
Sは空ではない閉じた凸集合であり、$ y \ notin S $であるため、最も近い点定理により、次のような一意の最小化点$ \ hat {x} \ in S $が存在します。
$ \ left(x- \ hat {x} \ right)^ T \ left(y- \ hat {x} \ right)\ leq 0 \ forall x \ in S $
$ p = \ left(y- \ hat {x} \ right)\ neq 0 $および$ \ beta = \ hat {x} ^ T \ left(y- \ hat {x} \ right)= p ^ Tとします。 \ hat {x} $。
次に、$ \ left(x- \ hat {x} \ right)^ T \ left(y- \ hat {x} \ right)\ leq 0 $
$ \ Rightarrow \ left(y- \ hat {x} \ right)^ T \ left(x- \ hat {x} \ right)\ leq 0 $
$ \ Rightarrow \ left(y- \ hat {x} \ right)^ Tx \ leq \ left(y- \ hat {x} \ right)^ T \ hat {x} = \ hat {x} ^ T \ left (y- \ hat {x} \ right)$つまり、$ p ^ Tx \ leq \ beta $
また、$ p ^ Ty- \ beta = \ left(y- \ hat {x} \ right)^ Ty- \ hat {x} ^ T \ left(y- \ hat {x} \ right)$
$ = \ left(y- \ hat {x} \ right)^ T \ left(yx \ right)= \ left \ | y- \ hat {x} \ right \ | ^ {2}> 0 $
$ \ Rightarrow p ^ Ty> \ beta $
この定理により、超平面が分離されます。上記の定理に基づく超平面は、次のように定義できます。
$ S_1 $と$ S_2 $を$ \ mathbb {R} $の空でないサブセットとし、$ H = \ left \ {X:A ^ TX = b \ right \} $を超平面とします。
$ A ^ TX \ leq b \ forall X \ in S_1 $と$ A_TX \ geq b \ forall X \ in S_2 $の場合、超平面Hは$ S_1 $と$ S_2 $を分離すると言われます。
$ A ^ TX <b \ forall X \ in S_1 $と$ A_TX> b \ forall X \ in S_2 $の場合、超平面Hは$ S_1 $と$ S_2 $を厳密に分離すると言われています
$ A ^ TX \ leq b \ forall X \ in S_1 $と$ A_TX \ geq b + \ varepsilon \ forall X \ in S_2 $の場合、超平面Hは$ S_1 $と$ S_2 $を強く分離すると言われます。ここで、$ \ varepsilon $は正のスカラーです。
$ \ mathbb {R} ^ n $の空でない集合Cは、$ x \ in C \ Rightarrow \ lambda x \ in C \ forall \ lambda \ geq 0 $の場合、頂点0の円錐であると言われます。
集合Cは、円錐であると同時に凸である場合、凸錐です。
たとえば、$ y = \ left | x \ right | $は凸錐ではないため、凸錐ではありません。
しかし、$ y \ geq \ left | x \ right | $は、円錐であると同時に凸であるため、凸錐です。
Note −円錐Cは、$ x、y \ in C、x + y \ in C $の場合に限り、凸です。
証明
Cは円錐であるため、$ x、y \ in C \ Rightarrow \ lambda x \ in C $および$ \ mu y \ in C \:\ forall \:\ lambda、\ mu \ geq 0 $の場合
$ \ lambda x + \ left(1- \ lambda \ right)y \ in C \:\ forall \:\ lambda \ in \ left(0、1 \ right)$の場合、Cは凸です。
Cは円錐なので、$ \ lambda x \ in C $および$ \ left(1- \ lambda \ right)y \ in C \ Leftrightarrow x、y \ in C $
したがって、$ x + y \ in C $の場合、Cは凸です。
一般に、$ x_1、x_2 \ in C $の場合、$ \ lambda_1x_1 + \ lambda_2x_2 \ in C、\ forall \ lambda_1、\ lambda_2 \ geq 0 $
例
$ \ mathbb {R} ^ n $内のベクトルの無限セットの円錐曲線は、凸錐です。
空のセットはすべて凸錐です。
一次関数はすべて凸錐です。
超平面は線形であるため、凸錐でもあります。
閉じた半空間も凸錐です。
Note − 2つの凸錐の交点は凸錐ですが、それらの結合は凸錐である場合とそうでない場合があります。
Sを$ \ mathbb {R} ^ n $の空でない集合とすると、$ S ^ * $で表されるSの極錐は$ S ^ * = \ left \ {p \ in \ mathbb {Rで与えられます。 } ^ n、p ^ Tx \ leq 0 \:\ forall x \ in S \ right \} $。
リマーク
Sが凸でない場合でも、極円錐は常に凸です。
Sが空集合の場合、$ S ^ * = \ mathbb {R} ^ n $。
極性は、直交性の一般化と見なすことができます。
$ C \ subseteq \ mathbb {R} ^ n $とすると、Cの直交空間は$ C ^ \ perp = \ left \ {y \ in \ mathbb {R} ^ n:\ left \ langle x、yで表されます。 \ right \ rangle = 0 \ forall x \ in C \ right \} $。
補題
$ S、S_1 $と$ S_2 $を$ \ mathbb {R} ^ n $の空でない集合とすると、次のステートメントが真になります。
$ S ^ * $は閉じた凸錐です。
$ S \ subseteq S ^ {**} $ここで、$ S ^ {**} $は$ S ^ * $の極錐です。
$ S_1 \ subseteq S_2 \ Rightarrow S_ {2} ^ {*} \ subseteq S_ {1} ^ {*} $。
証明
Step 1 − $ S ^ * = \ left \ {p \ in \ mathbb {R} ^ n、p ^ Tx \ leq 0 \:\ forall \:x \ in S \ right \} $
$ x_1、x_2 \ in S ^ * \ Rightarrow x_ {1} ^ {T} x \ leq 0 $および$ x_ {2} ^ {T} x \ leq 0、\ forall x \ in S $
$ \ lambda \ in \ left(0、1 \ right)、\ left [\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right] ^ Tx = \ left [\ left(\ lambda x_1 \ right )^ T + \ left \ {\ left(1- \ lambda \ right)x_ {2} \ right \} ^ {T} \ right] x、\ forall x \ in S $
$ = \ left [\ lambda x_ {1} ^ {T} + \ left(1- \ lambda \ right)x_ {2} ^ {T} \ right] x = \ lambda x_ {1} ^ {T} x + \ left(1- \ lambda \ right)x_ {2} ^ {T} \ leq 0 $
したがって、$ \ lambda x_1 + \ left(1- \ lambda \ right)x_ {2} \ in S ^ * $
したがって、$ S ^ * $は凸集合です。
$ \ lambda \ geq 0、p ^ {T} x \ leq 0、\ forall \:x \ in S $の場合
したがって、$ \ lambda p ^ T x \ leq 0、$
$ \ Rightarrow \ left(\ lambda p \ right)^ T x \ leq 0 $
$ \ Rightarrow \ lambda p \ in S ^ * $
したがって、$ S ^ * $は円錐です。
$ S ^ * $を表示するには、閉じています。つまり、$ p_n \ rightarrow p $を$ n \ rightarrow \ infty $として表示するには、$ p \ in S ^ * $
$ \ forall x \ in S、p_ {n} ^ {T} xp ^ T x = \ left(p_n-p \ right)^ T x $
As $ p_n \ rightarrow p $ as $ n \ rightarrow \ infty \ Rightarrow \ left(p_n \ rightarrow p \ right)\ rightarrow 0 $
したがって、$ p_ {n} ^ {T} x \ rightarrow p ^ {T} x $。しかし、$ p_ {n} ^ {T} x \ leq 0、\:\ forall x \ in S $
したがって、$ p ^ Tx \ leq 0、\ forall x \ in S $
$ \ Rightarrow p \ in S ^ * $
したがって、$ S ^ * $は閉じられます。
Step 2 − $ S ^ {**} = \ left \ {q \ in \ mathbb {R} ^ n:q ^ T p \ leq 0、\ forall p \ in S ^ * \ right \} $
$ x \ in S $、次に$ \ forall p \ in S ^ *、p ^ T x \ leq 0 \ Rightarrow x ^ Tp \ leq 0 \ Rightarrow x \ in S ^ {**} $
したがって、$ S \ subseteq S ^ {**} $
Step 3 − $ S_2 ^ * = \ left \ {p \ in \ mathbb {R} ^ n:p ^ Tx \ leq 0、\ forall x \ in S_2 \ right \} $
$ S_1 \ subseteq S_2 \ Rightarrow \ forall x \ in S_2 \ Rightarrow \ forall x \ in S_1 $以降
したがって、$ \ hat {p} \ in S_2 ^ *の場合、$ then $ \ hat {p} ^ Tx \ leq 0、\ forall x \ in S_2 $
$ \ Rightarrow \ hat {p} ^ Tx \ leq 0、\ forall x \ in S_1 $
$ \ Rightarrow \ hat {p} ^ T \ in S_1 ^ * $
$ \ Rightarrow S_2 ^ * \ subseteq S_1 ^ * $
定理
Cを空でない閉じた凸錐とすると、$ C = C ^ ** $
証明
前の補題による$ C = C ^ {**} $。
証明するには:$ x \ in C ^ {**} \ subseteq C $
$ x \ in C ^ {**} $とし、$ x \ notin C $
次に、基本的な分離定理により、ベクトル$ p \ neq 0 $とスカラー$ \ alpha $が存在し、$ p ^ Ty \ leq \ alpha、\ forall y \ in C $
したがって、$ p ^ Tx> \ alpha $
ただし、$ \ left(y = 0 \ right)\ in C $および$ p ^ Ty \ leq \ alphaであるため、\ forall y \ in C \ Rightarrow \ alpha \ geq 0 $および$ p ^ Tx> 0 $
$ p \ notin C ^ * $の場合、$ p ^ T \ bar {y}> 0 $および$ p ^ T \ left(\ lambda \ bar)のような$ \ bar {y} \ in C $が存在します。 {y} \ right)$は、$ \ lambda $を十分に大きくすることで、任意に大きくすることができます。
これは、$ p ^ Ty \ leq \ alpha、\ forall y \ in C $という事実と矛盾します。
したがって、$ p \ in C ^ * $
$ x \ in C ^ * = \ left \ {q:q ^ Tp \ leq 0なので、\ forall p \ in C ^ * \ right \} $
したがって、$ x ^ Tp \ leq 0 \ Rightarrow p ^ Tx \ leq 0 $
しかし、$ p ^ Tx> \ alpha $
したがって、矛盾です。
したがって、$ x \ in C $
したがって、$ C = C ^ {**} $です。
$ \ alpha_1x_1 + \ alpha_2x_2 + .... + \ alpha_nx_n $と$ \ alpha_1、\ alpha_2、...、\ alpha_n \ geq 0 $の形式の点は、$ x_1、x_2、...、の円錐曲線の組み合わせと呼ばれます。 x_n。$
$ x_i $が凸錐Cにある場合、$ x_i $のすべての円錐曲線もCにあります。
セットCは、その要素のすべての円錐曲線を含む場合、凸錐です。
コニックハル
円錐曲線の船体は、与えられた集合Sのすべての円錐曲線の組み合わせの集合として定義され、coni(S)で表されます。
したがって、$ coni \ left(S \ right)= \ left \ {\ displaystyle \ sum \ limits_ {i = 1} ^ k \ lambda_ix_i:x_i \ in S、\ lambda_i \ in \ mathbb {R}、\ lambda_i \ geq 0、i = 1,2、... \ right \} $
- 円錐形の船体は凸集合です。
- 原点は常に円錐の船体に属します。
$ \ mathbb {R} ^ n $の集合は、有限数の閉じた半空間の共通部分である場合、多面体であると言われます。
$ S = \ left \ {x \ in \ mathbb {R} ^ n:p_ {i} ^ {T} x \ leq \ alpha_i、i = 1,2、....、n \ right \} $
例えば、
$ \ left \ {x \ in \ mathbb {R} ^ n:AX = b \ right \} $
$ \ left \ {x \ in \ mathbb {R} ^ n:AX \ leq b \ right \} $
$ \ left \ {x \ in \ mathbb {R} ^ n:AX \ geq b \ right \} $
多面体コーン
$ \ mathbb {R} ^ n $の集合は、原点を含む有限数の半空間の共通部分である場合、つまり$ S = \ left \ {x \ in \ mathbb {の場合、多面体円錐であると言われます。 R} ^ n:p_ {i} ^ {T} x \ leq 0、i = 1、2、... \ right \} $
ポリトープ
ポリトープは、有界の多面体セットです。
備考
- ポリトープは、有限の点のセットの凸包です。
- 多面体円錐は、有限のベクトルセットによって生成されます。
- 多面体セットは閉集合です。
- 多面体セットは凸集合です。
Sを$ \ mathbb {R} ^ n $の凸集合とします。$ x = \ lambda x_1 + \ left(1- \ lambda \ right)x_2 $と$ x_1、x_2 \ in S $、および$ \ lambda \の場合、ベクトル$ x \ in S $はSの極値点であると言われます。 in \ left(0、1 \ right)\ Rightarrow x = x_1 = x_2 $。
例
Step 1 − $ S = \ left \ {\ left(x_1、x_2 \ right)\ in \ mathbb {R} ^ 2:x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 1 \ right \ } $
極値、$ E = \ left \ {\ left(x_1、x_2 \ right)\ in \ mathbb {R} ^ 2:x_ {1} ^ {2} + x_ {2} ^ {2} = 1 \ right \} $
Step 2 − $ S = \ left \ {\ left(x_1、x_2 \ right)\ in \ mathbb {R} ^ 2:x_1 + x_2 <2、-x_1 + 2x_2 \ leq 2、x_1、x_2 \ geq 0 \ right \ } $
極値、$ E = \ left \ {\ left(0、0 \ right)、\ left(2、0 \ right)、\ left(0、1 \ right)、\ left(\ frac {2} {3 }、\ frac {4} {3} \ right)\ right \} $
Step 3 − Sは、点$ \ left \ {\ left(0,0 \ right)、\ left(1,1 \ right)、\ left(1,3 \ right)、\ left(-2、 4 \ right)、\ left(0,2 \ right)\ right \} $
極値、$ E = \ left \ {\ left(0,0 \ right)、\ left(1,1 \ right)、\ left(1,3 \ right)、\ left(-2,4 \ right) \ right \} $
備考
凸集合Sの任意の点は、その極値の凸結合として表すことができます。
これは、$ \ mathbb {R} ^ n $の閉じた有界集合にのみ当てはまります。
無制限のセットには当てはまらない場合があります。
k極値
凸集合内の点は、それがS内のk次元凸集合の内部点であり、S内の(k + 1)次元凸集合の内部点ではない場合に限り、k極値と呼ばれます。基本的に、凸集合Sの場合、k個の極値点がk次元の開いた面になります。
Sを$ \ mathbb {R} ^ n $の閉じた凸集合とします。ゼロ以外のベクトル$ d \ in \ mathbb {R} ^ n $は、$ x \ in S、x + \ lambda d \ in S、\ forall \ lambda \ geq 0. $ごとに、Sの方向と呼ばれます。
$ d \ neq \ alpha d_2 $が$ \ alpha> 0 $の場合、Sの2つの方向$ d_1 $と$ d_2 $は別個と呼ばれます。
$ S $の方向$ d $は、2つの異なる方向の正の線形結合として記述できない場合、つまり$ \ lambda _1、\に対して$ d = \ lambda _1d_1 + \ lambda _2d_2 $の場合、極端な方向であると言われます。 lambda _2> 0 $、次に$ d_1 = \ alpha d_2 $ for some $ \ alpha $。
その他の方向は、極端な方向の正の組み合わせとして表すことができます。
凸集合$ S $の場合、一部の$ x \ in S $およびすべての$ \ lambda \ geq0 $に対して$ x + \ lambda d \ in S $となる方向dが呼び出されます。 recessive $ S $で。
$ \ mathbb {R} ^ n $の空でない凸集合S上の特定の関数$ f:S \ rightarrow $が最大に達する点の集合をEとすると、$ E $はの露出面と呼ばれます。 $ S $。露出面の方向は露出方向と呼ばれます。
方向が極端な方向である光線は、極端な光線と呼ばれます。
例
関数$ f \ left(x \ right)= y = \ left | x \ right | $について考えてみます。ここで、$ x \ in \ mathbb {R} ^ n $です。dを$ \ mathbb {R} ^ n $の単位ベクトルとします。
次に、dは関数fの方向です。これは、任意の$ \ lambda \ geq 0に対して、x + \ lambda d \ in f \ left(x \ right)$であるためです。
$ f:S \ rightarrow \ mathbb {R} $とします。ここで、Sは$ \ mathbb {R} ^ n $に設定された空でない凸であり、$ f \ left(x \ right)$はS上で凸であると言われます。 if $ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)\ leq \ lambda f \ left(x_1 \ right)+ \ left(1- \ lambda \ right)f \ left( x_2 \ right)、\ forall \ lambda \ in \ left(0,1 \ right)$。
一方、$ f:S \ rightarrow \ mathbb {R} $とします。ここで、Sは$ \ mathbb {R} ^ n $に設定された空でない凸集合であり、$ f \ left(x \ right)$と言います。 $ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)\ geq \ lambda f \ left(x_1 \ right)+ \ left(1- \ lambda \ right)の場合、S上で凹型になります)f \ left(x_2 \ right)、\ forall \ lambda \ in \ left(0、1 \ right)$。
$ f:S \ rightarrow \ mathbb {R} $とします。ここで、Sは$ \ mathbb {R} ^ n $に設定された空でない凸であり、$ f \ left(x \ right)$はS上で厳密に凸であると言われます。 if $ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)<\ lambda f \ left(x_1 \ right)+ \ left(1- \ lambda \ right)f \ left(x_2 \ right)、\ forall \ lambda \ in \ left(0、1 \ right)$。
$ f:S \ rightarrow \ mathbb {R} $とします。ここで、Sは$ \ mathbb {R} ^ n $に設定された空でない凸集合であり、$ f \ left(x \ right)$はS上で厳密に凹であると言われます。 if $ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)> \ lambda f \ left(x_1 \ right)+ \ left(1- \ lambda \ right)f \ left(x_2 \ right)、\ forall \ lambda \ in \ left(0、1 \ right)$。
例
一次関数は凸面と凹面の両方です。
$ f \ left(x \ right)= \ left | x \ right | $は凸関数です。
$ f \ left(x \ right)= \ frac {1} {x} $は凸関数です。
定理
$ f_1、f_2、...、f_k:\ mathbb {R} ^ n \ rightarrow \ mathbb {R} $を凸関数とします。関数$ f \ left(x \ right)= \ displaystyle \ sum \ limits_ {j = 1} ^ k \ alpha_jf_j \ left(x \ right)$を考えてみましょう。ここで$ \ alpha_j> 0、j = 1、2,。 ..k、$の場合、$ f \ left(x \ right)$は凸関数です。
証明
$ f_1、f_2、... f_k $は凸関数なので、
したがって、$ f_i \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)\ leq \ lambda f_i \ left(x_1 \ right)+ \ left(1- \ lambda \ right)f_i \ left (x_2 \ right)、\ forall \ lambda \ in \ left(0、1 \ right)$および$ i = 1、2、....、k $
関数$ f \ left(x \ right)$について考えてみます。
したがって、
$ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)$
$ = \ displaystyle \ sum \ limits_ {j = 1} ^ k \ alpha_jf_j \ left(\ lambda x_1 + 1- \ lambda \ right)x_2 \ leq \ displaystyle \ sum \ limits_ {j = 1} ^ k \ alpha_j \ラムダf_j \ left(x_1 \ right)+ \ left(1- \ lambda \ right)f_j \ left(x_2 \ right)$
$ \ Rightarrow f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)\ leq \ lambda \ left(\ displaystyle \ sum \ limits_ {j = 1} ^ k \ alpha _jf_j \ left( x_1 \ right)\ right)+ \ left(\ displaystyle \ sum \ limits_ {j = 1} ^ k \ alpha _jf_j \ left(x_2 \ right)\ right)$
$ \ Rightarrow f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)\ leq \ lambda f \ left(x_2 \ right)\ leq \ left(1- \ lambda \ right)f \左(x_2 \ right)$
したがって、$ f \ left(x \ right)$は凸関数です。
定理
$ f \ left(x \ right)$を凸集合$ S \ subset \ mathbb {R} ^ n $の凸関数とすると、Sの$ f \ left(x \ right)$の極小値はグローバル最小値。
証明
$ \ hat {x} $を$ f \ left(x \ right)$の極小値とし、$ \ hat {x} $は大域的最小値ではありません。
したがって、$ \は、$ f \ left(\ bar {x} \ right)<f \ left(\ hat {x} \ right)$となるようにS $に\ hat {x} \が存在します。
$ \ hat {x} $は極小値であるため、$ f \ left(\ hat {x} \ right)\ leqfのような近隣$ N_ \ varepsilon \ left(\ hat {x} \ right)$が存在します。 \ left(x \ right)、\ forall x \ in N_ \ varepsilon \ left(\ hat {x} \ right)\ cap S $
ただし、$ f \ left(x \ right)$はSの凸関数であるため、$ \ lambda \ in \ left(0、1 \ right)$の場合
$ \ lambda \ hat {x} + \ left(1- \ lambda \ right)\ bar {x} \ leq \ lambda f \ left(\ hat {x} \ right)+ \ left(1- \ lambda \ right)f \ left(\ bar {x} \ right)$
$ \ Rightarrow \ lambda \ hat {x} + \ left(1- \ lambda \ right)\ bar {x} <\ lambda f \ left(\ hat {x} \ right)+ \ left(1- \ lambda \右)f \ left(\ hat {x} \ right)$
$ \ Rightarrow \ lambda \ hat {x} + \ left(1- \ lambda \ right)\ bar {x} <f \ left(\ hat {x} \ right)、\ forall \ lambda \ in \ left(0 、1 \ right)$
しかし、いくつかの$ \ lambda <1 $で、1に近い場合、
$ \ lambda \ hat {x} + \ left(1- \ lambda \ right)\ bar {x} \ in N_ \ varepsilon \ left(\ hat {x} \ right)\ cap S $および$ f \ left( \ lambda \ hat {x} + \ left(1- \ lambda \ right)\ bar {x} \ right)<f \ left(\ bar {x} \ right)$
これは矛盾です。
したがって、$ \ bar {x} $はグローバルな最小値です。
碑文
Sを$ \ mathbb {R} ^ n $の空でないサブセットとし、$ f:S \ rightarrow \ mathbb {R} $とすると、epi(f)または$ E_f $で示されるfのエピグラフはサブセットです。 $ E_f = \ left \ {\ left(x、\ alpha \ right):x \ in \ mathbb {R} ^ n、\ alpha \ in \ mathbb {で定義される$ \ mathbb {R} ^ n + 1 $のR}、f \ left(x \ right)\ leq \ alpha \ right \} $
ハイポグラフ
Sを$ \ mathbb {R} ^ n $の空でないサブセットとし、$ f:S \ rightarrow \ mathbb {R} $とすると、hyp(f)または$ H_f = \ leftで表されるfのハイポグラフ\ {\ left(x、\ alpha \ right):x \ in \ mathbb {R} ^ n、\ alpha \ in \ mathbb {R} ^ n、\ alpha \ in \ mathbb {R}、f \ left( x \ right)\ geq \ alpha \ right \} $
定理
Sを$ \ mathbb {R} ^ n $の空でない凸集合とし、$ f:S \ rightarrow \ mathbb {R} ^ n $とすると、エピグラフ$ E_f $がである場合に限り、fは凸になります。凸集合。
証明
fを凸関数とします。
$ E_f $を表示することは、凸集合です。
$ \ left(x_1、\ alpha_1 \ right)、\ left(x_2、\ alpha_2 \ right)\ in E_f、\ lambda \ in \ left(0、1 \ right)$
$ \ lambda \ left(x_1、\ alpha_1 \ right)+ \ left(1- \ lambda \ right)\ left(x_2、\ alpha_2 \ right)\ in E_f $を表示するには
$ \ Rightarrow \ left [\ lambda x_1 + \ left(1- \ lambda \ right)x_2、\ lambda \ alpha_1 + \ left(1- \ lambda \ right)\ alpha_2 \ right] \ in E_f $
$ f \ left(x_1 \ right)\ leq \ alpha _1、f \ left(x_2 \ right)\ leq \ alpha _2 $
したがって、$ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)\ leq \ lambda f \ left(x_1 \ right)+ \ left(1- \ lambda \ right)f \ left (x_2 \ right)$
$ \ Rightarrow f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)\ leq \ lambda \ alpha_1 + \ left(1- \ lambda \ right)\ alpha_2 $
コンバース
$ E_f $を凸集合とします。
fが凸であることを示す。
つまり、$ x_1、x_2 \ in S、\ lambda \ left(0、1 \ right)$かどうかを表示します
$ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)\ leq \ lambda f \ left(x_1 \ right)+ \ left(1- \ lambda \ right)f \ left(x_2 \ right)$
$ x_1、x_2 \ in S、\ lambda \ in \ left(0、1 \ right)、f \ left(x_1 \ right)、f \ left(x_2 \ right)\ in \ mathbb {R} $
$ E_f $は凸集合であるため、$ \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2、\ lambda f \ left(x_1 \ right)+ \ left(1- \ lambda \ right)\右)f \ left(x_2 \ right)\ in E_f $
したがって、$ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)\ leq \ lambda f \ left(x_1 \ right)+ \ left(1- \ lambda \ right)f \ left (x_2 \ right)$
Sを$ \ mathbb {R} ^ n $と$ f:S \ rightarrow \ mathbb {R} ^ n $の空でない凸集合とします。次に、各整数$ k> 0 $の場合に限り、fは凸です。
$ x_1、x_2、... x_k \ in S、\ displaystyle \ sum \ limits_ {i = 1} ^ k \ lambda_i = 1、\ lambda_i \ geq 0、\ forall i = 1,2、s、k $、 $ f \ left(\ displaystyle \ sum \ limits_ {i = 1} ^ k \ lambda_ix_i \ right)\ leq \ displaystyle \ sum \ limits_ {i = 1} ^ k \ lambda _if \ left(x \ right) $
証明
kの帰納法による。
$ k = 1:x_1 \ in S $したがって、$ \ lambda_i = 1 $であるため、$ f \ left(\ lambda_1 x_1 \ right)\ leq \ lambda_i f \ left(x_1 \ right)$。
$ k = 2:\ lambda_1 + \ lambda_2 = 1 $および$ x_1、x_2 \ in S $
したがって、$ \ lambda_1x_1 + \ lambda_2x_2 \ in S $
したがって、定義上、$ f \ left(\ lambda_1 x_1 + \ lambda_2 x_2 \ right)\ leq \ lambda _1f \ left(x_1 \ right)+ \ lambda _2f \ left(x_2 \ right)$
$ n <k $の場合にステートメントが真であるとします
したがって、
$ f \ left(\ lambda_1 x_1 + \ lambda_2 x_2 + .... + \ lambda_k x_k \ right)\ leq \ lambda_1 f \ left(x_1 \ right)+ \ lambda_2 f \ left(x_2 \ right)+ ... + \ lambda_k f \ left(x_k \ right)$
$ k = n + 1:$ $ x_1、x_2、.... x_n、x_ {n + 1} \ in S $および$ \ displaystyle \ sum \ limits_ {i = 1} ^ {n + 1} = 1 $
したがって、$ \ mu_1x_1 + \ mu_2x_2 + ....... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ in S $
したがって、$ f \ left(\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right)$
$ = f \ left(\ left(\ mu_1 + \ mu_2 + ... + \ mu_n \ right)\ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n} {\ mu_1 + \ mu_2 + \ mu_3} + \ mu_ {n + 1} x_ {n + 1} \ right)$
$ = f \ left(\ mu_y + \ mu_ {n + 1} x_ {n + 1} \ right)$ここで、$ \ mu = \ mu_1 + \ mu_2 + ... + \ mu_n $および
$ y = \ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n} {\ mu_1 + \ mu_2 + ... + \ mu_n} $および$ \ mu_1 + \ mu_ {n + 1} = 1、y \ in S $
$ \ Rightarrow f \ left(\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right)\ leq \ mu f \ left(y \ right)+ \ mu_ {n +1} f \ left(x_ {n + 1} \ right)$
$ \ Rightarrow f \ left(\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right)\ leq $
$ \ left(\ mu_1 + \ mu_2 + ... + \ mu_n \ right)f \ left(\ frac {\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n} {\ mu_1 + \ mu_2 + ... + \ mu_n} \ right) + \ mu_ {n + 1} f \ left(x_ {n + 1} \ right)$
$ \ Rightarrow f \ left(\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right)\ leq \ left(\ mu_1 + \ mu_2 + ... + \ mu_n \右)$
$ \ left [\ frac {\ mu_1} {\ mu_1 + \ mu_2 + ... + \ mu_n} f \ left(x_1 \ right)+ ... + \ frac {\ mu_n} {\ mu_1 + \ mu_2 + ... + \ mu_n} f \ left(x_n \ right)\ right] + \ mu_ {n + 1} f \ left(x_ {n + 1} \ right)$
$ \ Rightarrow f \ left(\ mu_1x_1 + \ mu_2x_2 + ... + \ mu_nx_n + \ mu_ {n + 1} x_ {n + 1} \ right)\ leq \ mu_1f \ left(x_1 \ right)+ \ mu_2f \ left( x_2 \ right)+ .... $
したがって、証明されました。
Sを$ \ mathbb {R} ^ n $の空でない開集合とすると、$ f:S \ rightarrow \ mathbb {R} $は、$ \ hat {x} \ in S $で微分可能であると言われます。勾配ベクトルと呼ばれるベクトル$ \ bigtriangledown f \ left(\ hat {x} \ right)$と、次のような関数$ \ alpha:\ mathbb {R} ^ n \ rightarrow \ mathbb {R} $が存在します。
$ f \ left(x \ right)= f \ left(\ hat {x} \ right)+ \ bigtriangledown f \ left(\ hat {x} \ right)^ T \ left(x- \ hat {x} \右)+ \左\ | x = \ hat {x} \ right \ | \ alpha \ left(\ hat {x}、x- \ hat {x} \ right)、\ forall x \ in S $ここで、
$ \ alpha \ left(\ hat {x}、x- \ hat {x} \ right)\ rightarrow 0 \ bigtriangledown f \ left(\ hat {x} \ right)= \ left [\ frac {\ partial f} {\ partial x_1} \ frac {\ partial f} {\ partial x_2} ... \ frac {\ partial f} {\ partial x_n} \ right] _ {x = \ hat {x}} ^ {T} $
定理
Sを$ \ mathbb {R} ^ n $の空でない開いた凸集合とし、$ f:S \ rightarrow \ mathbb {R} $をSで微分可能とします。次に、fは、$の場合に限り、凸です。 x_1、x_2 \ in S、\ bigtriangledown f \ left(x_2 \ right)^ T \ left(x_1-x_2 \ right)\ leq f \ left(x_1 \ right)-f \ left(x_2 \ right)$
証明
fを凸関数とします。つまり、$ x_1、x_2 \ in Sの場合、\ lambda \ in \ left(0、1 \ right)$
$ f \ left [\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right] \ leq \ lambda f \ left(x_1 \ right)+ \ left(1- \ lambda \ right)f \ left(x_2 \ right)$
$ \ Rightarrow f \ left [\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right] \ leq \ lambda \ left(f \ left(x_1 \ right)-f \ left(x_2 \ right)\ right )+ f \ left(x_2 \ right)$
$ \ Rightarrow \ lambda \ left(f \ left(x_1 \ right)-f \ left(x_2 \ right)\ right)\ geq f \ left(x_2 + \ lambda \ left(x_1-x_2 \ right)\ right)- f \ left(x_2 \ right)$
$ \ Rightarrow \ lambda \ left(f \ left(x_1 \ right)-f \ left(x_2 \ right)\ right)\ geq f \ left(x_2 \ right)+ \ bigtriangledown f \ left(x_2 \ right)^ T \ left(x_1-x_2 \ right)\ lambda + $
$ \左\ | \ lambda \ left(x_1-x_2 \ right)\ right \ | \ alpha \ left(x_2、\ lambda \ left(x_1-x_2 \ right)-f \ left(x_2 \ right)\ right)$
ここで、$ \ alpha \ left(x_2、\ lambda \ left(x_1-x_2 \ right)\ right)\ rightarrow 0 $ as $ \ lambda \ rightarrow 0 $
両側で$ \ lambda $で割ると、次のようになります。
$ f \ left(x_1 \ right)-f \ left(x_2 \ right)\ geq \ bigtriangledown f \ left(x_2 \ right)^ T \ left(x_1-x_2 \ right)$
コンバース
$ x_1、x_2 \ in S、\ bigtriangledown f \ left(x_2 \ right)^ T \ left(x_1-x_2 \ right)\ leq f \ left(x_1 \ right)-f \ left(x_2 \ right) $
fが凸であることを示すため。
Sは凸であるため、$ x_3 = \ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ in S、\ lambda \ in \ left(0、1 \ right)$
$ x_1なので、x_3 \ in S $、したがって
$ f \ left(x_1 \ right)-f \ left(x_3 \ right)\ geq \ bigtriangledown f \ left(x_3 \ right)^ T \ left(x_1 -x_3 \ right)$
$ \ Rightarrow f \ left(x_1 \ right)-f \ left(x_3 \ right)\ geq \ bigtriangledown f \ left(x_3 \ right)^ T \ left(x_1- \ lambda x_1- \ left(1- \ lambda \ right)x_2 \ right)$
$ \ Rightarrow f \ left(x_1 \ right)-f \ left(x_3 \ right)\ geq \ left(1- \ lambda \ right)\ bigtriangledown f \ left(x_3 \ right)^ T \ left(x_1-x_2 \ right)$
以来、$ x_2、x_3 \ in S $したがって、
$ f \ left(x_2 \ right)-f \ left(x_3 \ right)\ geq \ bigtriangledown f \ left(x_3 \ right)^ T \ left(x_2-x_3 \ right)$
$ \ Rightarrow f \ left(x_2 \ right)-f \ left(x_3 \ right)\ geq \ bigtriangledown f \ left(x_3 \ right)^ T \ left(x_2- \ lambda x_1- \ left(1- \ lambda \ right)x_2 \ right)$
$ \ Rightarrow f \ left(x_2 \ right)-f \ left(x_3 \ right)\ geq \ left(-\ lambda \ right)\ bigtriangledown f \ left(x_3 \ right)^ T \ left(x_1-x_2 \右)$
したがって、上記の式を組み合わせると、次のようになります。
$ \ lambda \ left(f \ left(x_1 \ right)-f \ left(x_3 \ right)\ right)+ \ left(1- \ lambda \ right)\ left(f \ left(x_2 \ right)-f \ left(x_3 \ right)\ right)\ geq 0 $
$ \ Rightarrow f \ left(x_3 \ right)\ leq \ lambda f \ left(x_1 \ right)+ \ left(1- \ lambda \ right)f \ left(x_2 \ right)$
定理
Sを$ \ mathbb {R} ^ n $の空でない開いた凸集合とし、$ f:S \ rightarrow \ mathbb {R} $をSで微分可能とし、fがSで凸であるのは、任意の$ x_1、x_2 \ in S、\ left(\ bigtriangledown f \ left(x_2 \ right)-\ bigtriangledown f \ left(x_1 \ right)\ right)^ T \ left(x_2-x_1 \ right)\ geq 0 $
証明
fを凸関数とし、前の定理を使用します。
$ \ bigtriangledown f \ left(x_2 \ right)^ T \ left(x_1-x_2 \ right)\ leq f \ left(x_1 \ right)-f \ left(x_2 \ right)$および
$ \ bigtriangledown f \ left(x_1 \ right)^ T \ left(x_2-x_1 \ right)\ leq f \ left(x_2 \ right)-f \ left(x_1 \ right)$
上記の2つの方程式を追加すると、次のようになります。
$ \ bigtriangledown f \ left(x_2 \ right)^ T \ left(x_1-x_2 \ right)+ \ bigtriangledown f \ left(x_1 \ right)^ T \ left(x_2-x_1 \ right)\ leq 0 $
$ \ Rightarrow \ left(\ bigtriangledown f \ left(x_2 \ right)-\ bigtriangledown f \ left(x_1 \ right)\ right)^ T \ left(x_1-x_2 \ right)\ leq 0 $
$ \ Rightarrow \ left(\ bigtriangledown f \ left(x_2 \ right)-\ bigtriangledown f \ left(x_1 \ right)\ right)^ T \ left(x_2-x_1 \ right)\ geq 0 $
コンバース
$ x_1、x_2 \ in S、\ left(\ bigtriangledown f \ left(x_2 \ right)-\ bigtriangledown f \ left(x_1 \ right)\ right)^ T \ left(x_2-x_1 \ right)\ geq 0 $
fが凸であることを示すため。
$ x_1、x_2 \ in S $とします。したがって、平均値の定理により、$ \ frac {f \ left(x_1 \ right)-f \ left(x_2 \ right)} {x_1-x_2} = \ bigtriangledown f \ left( x \ right)、x \ in \ left(x_1-x_2 \ right)\ Rightarrow x = \ lambda x_1 + \ left(1- \ lambda \ right)x_2 $ Sは凸集合であるため、
$ \ Rightarrow f \ left(x_1 \ right)-f \ left(x_2 \ right)= \ left(\ bigtriangledown f \ left(x \ right)^ T \ right)\ left(x_1-x_2 \ right)$
$ x、x_1 $の場合、私たちは知っています-
$ \ left(\ bigtriangledown f \ left(x \ right)-\ bigtriangledown f \ left(x_1 \ right)\ right)^ T \ left(x-x_1 \ right)\ geq 0 $
$ \ Rightarrow \ left(\ bigtriangledown f \ left(x \ right)-\ bigtriangledown f \ left(x_1 \ right)\ right)^ T \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2- x_1 \ right)\ geq 0 $
$ \ Rightarrow \ left(\ bigtriangledown f \ left(x \ right)-\ bigtriangledown f \ left(x_1 \ right)\ right)^ T \ left(1- \ lambda \ right)\ left(x_2-x_1 \ right )\ geq 0 $
$ \ Rightarrow \ bigtriangledown f \ left(x \ right)^ T \ left(x_2-x_1 \ right)\ geq \ bigtriangledown f \ left(x_1 \ right)^ T \ left(x_2-x_1 \ right)$
上記の式を組み合わせると、次のようになります。
$ \ Rightarrow \ bigtriangledown f \ left(x_1 \ right)^ T \ left(x_2-x_1 \ right)\ leq f \ left(x_2 \ right)-f \ left(x_1 \ right)$
したがって、最後の定理を使用すると、fは凸関数です。
2回微分可能関数
Sを$ \ mathbb {R} ^ n $の空でないサブセットとし、$ f:S \ rightarrow \ mathbb {R} $とすると、fは$ \ bar {x} \ inSで2回微分可能であると言われます。 $ベクトル$ \ bigtriangledown f \ left(\ bar {x} \ right)、\:nXn $行列$ H \ left(x \ right)$(ヘッセ行列と呼ばれる)および関数$ \ alphaが存在する場合: \ mathbb {R} ^ n \ rightarrow \ mathbb {R} $で、$ f \ left(x \ right)= f \ left(\ bar {x} + x- \ bar {x} \ right)= f \ left(\ bar {x} \ right)+ \ bigtriangledown f \ left(\ bar {x} \ right)^ T \ left(x- \ bar {x} \ right)+ \ frac {1} {2} \左(x- \ bar {x} \ right)H \ left(\ bar {x} \ right)\ left(x- \ bar {x} \ right)$
ここで、$ \ alpha \ left(\ bar {x}、x- \ bar {x} \ right)\ rightarrow Oasx \ rightarrow \ bar {x} $
定理
fを2回微分可能な関数とします。$ \ bar {x} $が極小値の場合、$ \ bigtriangledown f \ left(\ bar {x} \ right)= 0 $およびヘッセ行列$ H \ left(\ bar {x} \ right)$正の半定値です。
証明
$ d \ in \ mathbb {R} ^ n $とします。fは$ \ bar {x} $で2回微分可能であるため。
したがって、
$ f \ left(\ bar {x} + \ lambda d \ right)= f \ left(\ bar {x} \ right)+ \ lambda \ bigtriangledown f \ left(\ bar {x} \ right)^ T d + \ lambda ^ 2d ^ TH \ left(\ bar {x} \ right)d + \ lambda ^ 2d ^ TH \ left(\ bar {x} \ right)d + $
$ \ lambda ^ 2 \ left \ | d \ right \ | ^ 2 \ beta \ left(\ bar {x}、\ lambda d \ right)$
ただし、$ \ bigtriangledown f \ left(\ bar {x} \ right)= 0 $および$ \ beta \ left(\ bar {x}、\ lambda d \ right)\ rightarrow 0 $ as $ \ lambda \ rightarrow 0 $
$ \ Rightarrow f \ left(\ bar {x} + \ lambda d \ right)-f \ left(\ bar {x} \ right)= \ lambda ^ 2d ^ TH \ left(\ bar {x} \ right) d $
$ \ bar {x} $は極小値であるため、$ f \ left(x \ right)\ leq f \ left(\ bar {x} + \ lambda d \ rightのような$ \ delta> 0 $が存在します)、\ forall \ lambda \ in \ left(0、\ delta \ right)$
定理
$ f:S \ rightarrow \ mathbb {R} ^ n $とします。ここで、$ S \ subset \ mathbb {R} ^ n $はSに対して2回微分可能です。$ \ bigtriangledownf \ left(x \ right)= 0 $および$ H \ left(\ bar {x} \ right)$は、すべての$ x \ in S $に対して正の半確定であり、$ \ bar {x} $はグローバルな最適解です。
証明
$ H \ left(\ bar {x} \ right)$は正の半確定であるため、fはS上の凸関数です。fは微分可能であり、$ \ bar {x} $で凸であるため
$ \ bigtriangledown f \ left(\ bar {x} \ right)^ T \ left(x- \ bar {x} \ right)\ leq f \ left(x \ right)-f \ left(\ bar {x} \ right)、\ forall x \ in S $
$ \ bigtriangledown f \ left(\ bar {x} \ right)= 0なので、f \ left(x \ right)\ geq f \ left(\ bar {x} \ right)$
したがって、$ \ bar {x} $はグローバルな最適値です。
定理
$ \ bar {x} \ in S $が問題$ f:S \ rightarrow \ mathbb {R} $の局所最適解であると仮定します。ここで、Sは$ \ mathbb {R} ^ n $の空でないサブセットです。 Sは凸です。$ min \:f \ left(x \ right)$ここで、$ x \ in S $です。
次に:
$ \ bar {x} $は、グローバルな最適解です。
$ \ bar {x} $が厳密に極小値であるか、fが厳密に凸関数である場合、$ \ bar {x} $は一意のグローバル最適解であり、強力な極小値でもあります。
証明
$ \ bar {x} $を、$ x \ neq \ bar {x} $および$ f \ left(\ bar {x} \ right)= f \ left(\ hat {)のような、問題に対する別のグローバルな最適解とします。 x} \ right)$
$ \ hat {x}、\ bar {x} \ in S $およびSは凸であるため、$ \ frac {\ hat {x} + \ bar {x}} {2} \ in S $およびfは厳密に凸。
$ \ Rightarrow f \ left(\ frac {\ hat {x} + \ bar {x}} {2} \ right)<\ frac {1} {2} f \ left(\ bar {x} \ right)+ \ frac {1} {2} f \ left(\ hat {x} \ right)= f \ left(\ hat {x} \ right)$
これは矛盾です。
したがって、$ \ hat {x} $は独自のグローバル最適ソリューションです。
当然の結果
$ f:S \ subset \ mathbb {R} ^ n \ rightarrow \ mathbb {R} $を微分可能な凸関数とします。ここで、$ \ phi \ neq S \ subset \ mathbb {R} ^ n $は凸集合です。$ min f \ left(x \ right)、x \ in S $の問題を考えてみましょう。$ \ bigtriangledownf \ left(\ bar {x} \ right)^ Tの場合、$ \ bar {x} $が最適解です。 \ left(x- \ bar {x} \ right)\ geq 0、\ forall x \ in S. $
証明
$ \ bar {x} $が最適解であるとします。つまり、$ f \ left(\ bar {x} \ right)\ leq f \ left(x \ right)、\ forall x \ in S $
$ \ Rightarrow f \ left(x \ right)= f \ left(\ bar {x} \ right)\ geq 0 $
$ f \ left(x \ right)= f \ left(\ bar {x} \ right)+ \ bigtriangledown f \ left(\ bar {x} \ right)^ T \ left(x- \ bar {x} \右)+ \左\ | x- \ bar {x} \ right \ | \ alpha \ left(\ bar {x}、x- \ bar {x} \ right)$
ここで、$ \ alpha \ left(\ bar {x}、x- \ bar {x} \ right)\ rightarrow 0 $ as $ x \ rightarrow \ bar {x} $
$ \ Rightarrow f \ left(x \ right)-f \ left(\ bar {x} \ right)= \ bigtriangledown f \ left(\ bar {x} \ right)^ T \ left(x- \ bar {x } \ right)\ geq 0 $
当然の結果
fを$ \ bar {x} $で微分可能な凸関数とすると、$ \ bigtriangledown f \ left(\ bar {x} \ right)= 0 $の場合、$ \ bar {x} $はグローバル最小値になります。
例
$ f \ left(x \ right)= \ left(x ^ 2-1 \ right)^ {3}、x \ in \ mathbb {R} $。
$ \ bigtriangledown f \ left(x \ right)= 0 \ Rightarrow x = -1,0,1 $。
$ \ bigtriangledown ^ 2f \ left(\ pm 1 \ right)= 0、\ bigtriangledown ^ 2 f \ left(0 \ right)= 6> 0 $。
$ f \ left(\ pm 1 \ right)= 0、f \ left(0 \ right)=-1 $
したがって、$ f \ left(x \ right)\ geq -1 = f \ left(0 \ right)\ Rightarrow f \ left(0 \ right)\ leq f \ left(x \ right)\ forall x \ in \ mathbb {R} $
$ f \ left(x \ right)= x \ log x $は$ S = \ left \ {x \ in \ mathbb {R}、x> 0 \ right \} $で定義されています。
$ {f} 'x = 1 + \ log x $
$ {f} '' x = \ frac {1} {x}> 0 $
したがって、この関数は厳密に凸です。
$ f \ left(x \ right)= e ^ {x}、x \ in \ mathbb {R} $は厳密に凸です。
$ f:S \ rightarrow \ mathbb {R} $とします。ここで、$ S \ subset \ mathbb {R} ^ n $は空でない凸集合です。各$ x_1、x_2 \ in S $に対して、$ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)\ leq max \ left \がある場合、関数fは準凸であると言われます。 {f \ left(x_1 \ right)、f \ left(x_2 \ right)\ right \}、\ lambda \ in \ left(0、1 \ right)$
たとえば、$ f \ left(x \ right)= x ^ {3} $
$ f:S \ rightarrow R $とします。ここで、$ S \ subset \ mathbb {R} ^ n $は空でない凸集合です。各$ x_1、x_2 \ in S $に対して、$ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)\ geq min \ left \がある場合、関数fは準凸であると言われます。 {f \ left(x_1 \ right)、f \ left(x_2 \ right)\ right \}、\ lambda \ in \ left(0、1 \ right)$
備考
- すべての凸関数は準凸ですが、その逆は当てはまりません。
- 準凸と準凸の両方である関数は、準単調と呼ばれます。
定理
$ f:S \ rightarrow \ mathbb {R} $とし、Sは$ \ mathbb {R} ^ n $の空でない凸集合です。関数fは、$ S _ {\ alpha} = \ left(x \ in S:f \ left(x \ right)\ leq \ alpha \ right \} $が各実数\ alpha $に対して凸である場合に限り、準凸です。
証明
fをSの準凸とします。
$ x_1、x_2 \ in S _ {\ alpha} $とすると、$ x_1、x_2 \ in S $と$ max \ left \ {f \ left(x_1 \ right)、f \ left(x_2 \ right)\ right \} \ leq \ alpha $
$ \ lambda \ in \ left(0、1 \ right)$とし、$ x = \ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ leq max \ left \ {f \ left(x_1 \ right) 、f \ left(x_2 \ right)\ right \} \ Rightarrow x \ in S $
したがって、$ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)\ leq max \ left \ {f \ left(x_1 \ right)、f \ left(x_2 \ right)\ right \} \ leq \ alpha $
したがって、$ S _ {\ alpha} $は凸です。
コンバース
$ S _ {\ alpha} $が各$ \ alpha $に対して凸であるとします。
$ x_1、x_2 \ in S、\ lambda \ in \ left(0,1 \ right)$
$ x = \ lambda x_1 + \ left(1- \ lambda \ right)x_2 $
$ x = \ lambda x_1 + \ left(1- \ lambda \ right)x_2 $とします
$ x_1の場合、x_2 \ in S _ {\ alpha}、\ alpha = max \ left \ {f \ left(x_1 \ right)、f \ left(x_2 \ right)\ right \} $
$ \ Rightarrow \ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ in S _ {\ alpha} $
$ \ Rightarrow f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)\ leq \ alpha $
したがって、証明されました。
定理
$ f:S \ rightarrow \ mathbb {R} $とし、Sは$ \ mathbb {R} ^ n $の空でない凸集合です。関数fは、$ S _ {\ alpha} = \ left \ {x \ in S:f \ left(x \ right)\ geq \ alpha \ right \} $が各実数$ \に対して凸である場合にのみ準凹型です。 alpha $。
定理
$ f:S \ rightarrow \ mathbb {R} $とし、Sは$ \ mathbb {R} ^ n $の空でない凸集合です。関数fは、$ S _ {\ alpha} = \ left \ {x \ in S:f \ left(x \ right)= \ alpha \ right \} $が各実数$ \ alphaに対して凸である場合に限り、準単調です。 $。
定理
Sを$ \ mathbb {R} ^ n $の空でない凸集合とし、$ f:S \ rightarrow \ mathbb {R} $をSで微分可能とすると、fは、$ x_1、x_2の場合に限り、準凸になります。 \ in S $と$ f \ left(x_1 \ right)\ leq f \ left(x_2 \ right)$、$ \ bigtriangledown f \ left(x_2 \ right)^ T \ left(x_2-x_1 \ right) \ leq 0 $
証明
fを準凸関数とします。
$ x_1、x_2 \ in S $とし、$ f \ left(x_1 \ right)\ leq f \ left(x_2 \ right)$
$ x_2でのfの微分可能性により、\ lambda \ in \ left(0、1 \ right)$
$ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)= f \ left(x_2 + \ lambda \ left(x_1-x_2 \ right)\ right)= f \ left(x_2 \ right )+ \ bigtriangledown f \ left(x_2 \ right)^ T \ left(x_1-x_2 \ right)$
$ + \ lambda \ left \ | x_1-x_2 \ right \ | \ alpha \ left(x_2、\ lambda \ left(x_1-x_2 \ right)\ right)$
$ \ Rightarrow f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)-f \ left(x_2 \ right)-f \ left(x_2 \ right)= \ bigtriangledown f \ left(x_2 \ right)^ T \ left(x_1-x_2 \ right)$
$ + \ lambda \ left \ | x_1-x_2 \ right \ | \ alpha \ left(x2、\ lambda \ left(x_1-x_2 \ right)\ right)$
ただし、fは準凸であるため、$ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)\ leq f \ left(x_2 \ right)$
$ \ bigtriangledown f \ left(x_2 \ right)^ T \ left(x_1-x_2 \ right)+ \ lambda \ left \ | x_1-x_2 \ right \ | \ alpha \ left(x_2、\ lambda \ left(x_1、x_2 \ right)\ right)\ leq 0 $
しかし、$ \ alpha \ left(x_2、\ lambda \ left(x_1、x_2 \ right)\ right)\ rightarrow 0 $ as $ \ lambda \ rightarrow 0 $
したがって、$ \ bigtriangledown f \ left(x_2 \ right)^ T \ left(x_1-x_2 \ right)\ leq 0 $
コンバース
$ x_1、x_2 \ in S $および$ f \ left(x_1 \ right)\ leq f \ left(x_2 \ right)$、$ \ bigtriangledown f \ left(x_2 \ right)^ T \ left(x_1、 x_2 \ right)\ leq 0 $
fが準凸であることを示すには、$ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)\ leq f \ left(x_2 \ right)$
Proof by contradiction
$ x_3 = \ lambda x_1 + \ left(1- \ lambda \ right)x_2 $が存在し、$ f \ left(x_2 \ right)<f \ left(x_3 \ right)$が$ \ lambda \ inにあるとします。 \ left(0、1 \ right)$
$ x_2 $および$ x_3の場合、\ bigtriangledown f \ left(x_3 \ right)^ T \ left(x_2-x_3 \ right)\ leq 0 $
$ \ Rightarrow- \ lambda \ bigtriangledown f \ left(x_3 \ right)^ T \ left(x_2-x_3 \ right)\ leq 0 $
$ \ Rightarrow \ bigtriangledown f \ left(x_3 \ right)^ T \ left(x_1-x_2 \ right)\ geq 0 $
$ x_1 $および$ x_3の場合、\ bigtriangledown f \ left(x_3 \ right)^ T \ left(x_1-x_3 \ right)\ leq 0 $
$ \ Rightarrow \ left(1- \ lambda \ right)\ bigtriangledown f \ left(x_3 \ right)^ T \ left(x_1-x_2 \ right)\ leq 0 $
$ \ Rightarrow \ bigtriangledown f \ left(x_3 \ right)^ T \ left(x_1-x_2 \ right)\ leq 0 $
したがって、上記の式から、$ \ bigtriangledown f \ left(x_3 \ right)^ T \ left(x_1-x_2 \ right)= 0 $
$ U = \ left \ {x:f \ left(x \ right)\ leq f \ left(x_2 \ right)、x = \ mu x_2 + \ left(1- \ mu \ right)x_3、\ mu \ inを定義します\ left(0,1 \ right)\ right \} $
したがって、$ x_0 = \ mu_0 x_2 = \ mu x_2 + \ left(1- \ mu \ right)x_3 $ for some $ \ mu _0 \ in \ left(0,1 \ right)となるような$ x_0 \ in U $を見つけることができます。 )$は$ x_3 $と$ \ hat {x} \ in \ left(x_0、x_1 \ right)$に最も近く、平均値の定理により、
$$ \ frac {f \ left(x_3 \ right)-f \ left(x_0 \ right)} {x_3-x_0} = \ bigtriangledown f \ left(\ hat {x} \ right)$$
$$ \ Rightarrow f \ left(x_3 \ right)= f \ left(x_0 \ right)+ \ bigtriangledown f \ left(\ hat {x} \ right)^ T \ left(x_3-x_0 \ right)$$
$$ \ Rightarrow f \ left(x_3 \ right)= f \ left(x_0 \ right)+ \ mu_0 \ lambda f \ left(\ hat {x} \ right)^ T \ left(x_1-x_2 \ right)$ $
$ x_0 $は$ x_1 $と$ x_2 $および$ f \ left(x_2 \ right)<f \ left(\ hat {x} \ right)$の組み合わせであるため
開始手順を繰り返すことにより、$ \ bigtriangledown f \ left(\ hat {x} \ right)^ T \ left(x_1-x_2 \ right)= 0 $
したがって、上記の方程式を組み合わせると、次のようになります。
$$ f \ left(x_3 \ right)= f \ left(x_0 \ right)\ leq f \ left(x_2 \ right)$$
$$ \ Rightarrow f \ left(x_3 \ right)\ leq f \ left(x_2 \ right)$$
したがって、それは矛盾です。
例
Step 1 − $ f \ left(x \ right)= X ^ 3 $
$ Let f \ left(x_1 \ right)\ leq f \ left(x_2 \ right)$
$ \ Rightarrow x_ {1} ^ {3} \ leq x_ {2} ^ {3} \ Rightarrow x_1 \ leq x_2 $
$ \ bigtriangledown f \ left(x_2 \ right)\ left(x_1-x_2 \ right)= 3x_ {2} ^ {2} \ left(x_1-x_2 \ right)\ leq 0 $
したがって、$ f \ left(x \ right)$は準凸です。
Step 2 − $ f \ left(x \ right)= x_ {1} ^ {3} + x_ {2} ^ {3} $
$ \ hat {x_1} = \ left(2、-2 \ right)$および$ \ hat {x_2} = \ left(1、0 \ right)$とします。
したがって、$ f \ left(\ hat {x_1} \ right)= 0、f \ left(\ hat {x_2} \ right)= 1 \ Rightarrow f \ left(\ hat {x_1} \ right)\ setminus <f \ left(\ hat {x_2} \ right)$
したがって、$ \ bigtriangledown f \ left(\ hat {x_2} \ right)^ T \ left(\ hat {x_1}-\ hat {x_2} \ right)= \ left(3、0 \ right)^ T \ left (1、-2 \ right)= 3> 0 $
したがって、$ f \ left(x \ right)$は準凸ではありません。
$ f:S \ rightarrow \ mathbb {R} ^ n $およびSを$ \ mathbb {R} ^ n $の空でない凸集合とすると、各$ x_1、x_2に対して、fは厳密に準凸関数であると言われます。 \ in S $ with $ f \ left(x_1 \ right)\ neq f \ left(x_2 \ right)$、$ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right) <max \:\ left \ {f \ left(x_1 \ right)、f \ left(x_2 \ right)\ right \} $
備考
- すべての厳密な準凸関数は厳密に凸です。
- 厳密に準凸関数は準凸を意味しません。
- 厳密に準凸関数は強く準凸ではない場合があります。
- 疑似凸関数は厳密に準凸関数です。
定理
$ f:S \ rightarrow \ mathbb {R} ^ n $を厳密に準凸関数とし、Sを$ \ mathbb {R} ^ n $の空でない凸集合とします。問題を考えてみましょう:$ min \:f \ left (x \ right)、x \ in S $。$ \ hat {x} $がローカル最適解である場合、$ \ bar {x} $はグローバル最適解です。
証明
$ f \ left(\ bar {x} \ right)\ leq f \ left(\ hat {x} \ right)$のような$ \ bar {x} \ in S $が存在するとします。
$ \ bar {x}、\ hat {x} \ in S $およびSは凸集合であるため、したがって、
$$ \ lambda \ bar {x} + \ left(1- \ lambda \ right)\ hat {x} \ in S、\ forall \ lambda \ in \ left(0,1 \ right)$$
$ \ hat {x} $は極小値であるため、$ f \ left(\ hat {x} \ right)\ leq f \ left(\ lambda \ bar {x} + \ left(1- \ lambda \ right)\ hat {x} \ right)、\ forall \ lambda \ in \ left(0、\ delta \ right)$
fは厳密に準凸であるため。
$$ f \ left(\ lambda \ bar {x} + \ left(1- \ lambda \ right)\ hat {x} \ right)<max \ left \ {f \ left(\ hat {x} \ right) 、f \ left(\ bar {x} \ right)\ right \} = f \ left(\ hat {x} \ right)$$
したがって、それは矛盾です。
厳密に準凹関数
$ f:S \ rightarrow \ mathbb {R} ^ n $およびSを$ \ mathbb {R} ^ n $の空でない凸集合とすると、各$ x_1に対して、fは厳密に準凸関数になるようにsaudされます。 x_2 \ in S $ with $ f \ left(x_1 \ right)\ neq f \ left(x_2 \ right)$、
$$ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)> min \ left \ {f \ left(x_1 \ right)、f \ left(x_2 \ right)\ right \} $$。
例
$ f \ left(x \ right)= x ^ 2-2 $
定義域$ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)の制約を満たすドメイン内の任意の2点$ x_1、x_2 $を取る場合、これは厳密に準凸関数です。 <max \ left \ {f \ left(x_1 \ right)、f \ left(x_2 \ right)\ right \} $関数が負のx軸で減少し、正のx軸で増加しているため(放物線なので)。
$ f \ left(x \ right)=-x ^ 2 $
これは厳密な準凸関数ではありません。$ x_1 = 1 $と$ x_2 = -1 $と$ \ lambda = 0.5 $を取ると、$ f \ left(x_1 \ right)=-1 = f \ left( x_2 \ right)$しかし$ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)= 0 $したがって、定義に記載されている条件を満たしていません。しかし、定義域内の任意の2つの点をとると、定義域$ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)> min \ left \の制約を満たすため、これは準凹関数です。 {f \ left(x_1 \ right)、f \ left(x_2 \ right)\ right \} $。関数が負のx軸で増加し、正のx軸で減少しているため。
$ f:S \ rightarrow \ mathbb {R} ^ n $とSを$ \ mathbb {R} ^ n $の空でない凸集合とすると、$ x_1、x_2 \ in Sの場合、fは強く準凸関数になります。 $ with $ \ left(x_1 \ right)\ neq \ left(x_2 \ right)$、$ f \ left(\ lambda x_1 + \ left(1- \ lambda \ right)x_2 \ right)<max \:\ left \ {f \ left(x_1 \ right)、f \ left(x_2 \ right)\ right \}、\ forall \ lambda \ in \ left(0,1 \ right)$
定理
$ \ mathbb {R} ^ n $の空でない凸集合S上の準凸関数$ f:S \ rightarrow \ mathbb {R} ^ n $は、いずれかを結ぶ線分で一定でない場合、強く準凸関数です。 Sのポイント。
証明
fを準凸関数とし、Sの任意の点を結ぶ線分で一定ではありません。
fが強く準凸関数ではないとします。
$ x_1、x_2 \ in S $と$ x_1 \ neq x_2 $が存在する
$$ f \ left(z \ right)\ geq max \ left \ {f \ left(x_1 \ right)、f \ left(x_2 \ right)\ right \}、\ forall z = \ lambda x_1 + \ left(1 -\ lambda \ right)x_2、\ lambda \ in \ left(0,1 \ right)$$
$ \ Rightarrow f \ left(x_1 \ right)\ leq f \ left(z \ right)$および$ f \ left(x_2 \ right)\ leq f \ left(z \ right)$
$ \ left [x_1、z \ right] $と$ \ left [z、x_2 \ right] $ではfが一定ではないため、
したがって、$ u \ in \ left [x_1、z \ right] $と$ v = \ left [z、x_2 \ right] $が存在します。
$$ \ Rightarrow u = \ mu_1x_1 + \ left(1- \ mu_1 \ right)z、v = \ mu_2z + \ left(1- \ mu_2 \ right)x_2 $$
fは準凸であるため、
$$ \ Rightarrow f \ left(u \ right)\ leq max \ left \ {f \ left(x_1 \ right)、f \ left(z \ right)\ right \} = f \ left(z \ right)\ :\:および\:\:f \ left(v \ right)\ leq max \ left \ {f \ left(z \ right)、f \ left(x_2 \ right)\ right \} $$
$$ \ Rightarrow f \ left(u \ right)\ leq f \ left(z \ right)\:\:and \:\:f \ left(v \ right)\ leq f \ left(z \ right)$ $
$$ \ Rightarrow max \ left \ {f \ left(u \ right)、f \ left(v \ right)\ right \} \ leq f \ left(z \ right)$$
しかし、zはuとvの間の任意の点であり、それらのいずれかが等しい場合、fは定数です。
したがって、$ max \ left \ {f \ left(u \ right)、f \ left(v \ right)\ right \} \ leq f \ left(z \ right)$
これは、fの準凸性を$ z \ in \ left [u、v \ right] $と矛盾します。
したがって、fは強く準凸関数です。
定理
$ f:S \ rightarrow \ mathbb {R} ^ n $とSを$ \ mathbb {R} ^ n $の空でない凸集合とします。$ \ hat {x} $がローカル最適解である場合、$ \ hat {x} $は一意のグローバル最適解です。
証明
強い準凸関数も厳密に準凸関数であるため、局所最適解は大域最適解です。
Uniqueness −fが2点でグローバル最適解を達成すると$ u、v \ in S $
$$ \ Rightarrow f \ left(u \ right)\ leq f \ left(x \ right)。\ forall x \ in S \:\:and \:\:f \ left(v \ right)\ leq f \左(x \ right)。\ forall x \ in S $$
uがグローバル最適解の場合、$ f \ left(u \ right)\ leq f \ left(v \ right)$および$ f \ left(v \ right)\ leq f \ left(u \ right)\ Rightarrow f \ left(u \ right)= f \ left(v \ right)$
$$ f \ left(\ lambda u + \ left(1- \ lambda \ right)v \ right)<max \ left \ {f \ left(u \ right)、f \ left(v \ right)\ right \} = f \ left(u \ right)$$
これは矛盾です。
したがって、グローバルな最適解は1つしかありません。
備考
- 強い準凸関数も厳密に準凸関数です。
- 厳密に凸な関数は、強く準凸である場合とそうでない場合があります。
- 微分可能な厳密な凸は、強く準凸です。
$ f:S \ rightarrow \ mathbb {R} $を微分可能関数とし、Sを$ \ mathbb {R} ^ n $の空でない凸集合とすると、各$ x_1に対して、fは疑似凸であると言われます。 x_2 \ in S $ with $ \ bigtriangledown f \ left(x_1 \ right)^ T \ left(x_2-x_1 \ right)\ geq 0 $、$ f \ left(x_2 \ right)\ geq f \ left( x_1 \ right)$、または同等に$ f \ left(x_1 \ right)> f \ left(x_2 \ right)$の場合$ \ bigtriangledown f \ left(x_1 \ right)^ T \ left(x_2-x_1 \ right )<0 $
疑似凹機能
$ f:S \ rightarrow \ mathbb {R} $を微分可能関数とし、Sを$ \ mathbb {R} ^ n $の空でない凸集合とすると、各$ x_1に対して、fは疑似凸であると言われます。 x_2 \ in S $ with $ \ bigtriangledown f \ left(x_1 \ right)^ T \ left(x_2-x_1 \ right)\ geq 0 $、$ f \ left(x_2 \ right)\ leq f \ left( x_1 \ right)$、または同等に$ f \ left(x_1 \ right)> f \ left(x_2 \ right)$の場合$ \ bigtriangledown f \ left(x_1 \ right)^ T \ left(x_2-x_1 \ right )> 0 $
備考
関数が疑似凸と疑似凹の両方である場合、は疑似線形と呼ばれます。
微分可能な凸関数も疑似凸です。
疑似凸関数は凸ではない場合があります。例えば、
$ f \ left(x \ right)= x + x ^ 3 $は凸ではありません。$ x_1 \ leq x_2、x_ {1} ^ {3} \ leq x_ {2} ^ {3} $の場合
したがって、$ \ bigtriangledown f \ left(x_1 \ right)^ T \ left(x_2-x_1 \ right)= \ left(1 + 3x_ {1} ^ {2} \ right)\ left(x_2-x_1 \ right) \ geq 0 $
そして、$ f \ left(x_2 \ right)-f \ left(x_1 \ right)= \ left(x_2-x_1 \ right)+ \ left(x_ {2} ^ {3} -x_ {1} ^ {3 } \ right)\ geq 0 $
$ \ Rightarrow f \ left(x_2 \ right)\ geq f \ left(x_1 \ right)$
したがって、それは擬凸です。
疑似凸関数は厳密に準凸です。したがって、疑似凸のすべての極小値も大域的最小値です。
厳密に疑似凸関数
$ f:S \ rightarrow \ mathbb {R} $を微分可能関数とし、Sを$ \ mathbb {R} ^ n $の空でない凸集合とすると、各$ x_1に対して、fは疑似凸であると言われます。 x_2 \ in S $ with $ \ bigtriangledown f \ left(x_1 \ right)^ T \ left(x_2-x_1 \ right)\ geq 0 $、$ f \ left(x_2 \ right)> f \ left(x_1 \ right)$、または同等に$ f \ left(x_1 \ right)\ geq f \ left(x_2 \ right)$ then $ \ bigtriangledown f \ left(x_1 \ right)^ T \ left(x_2-x_1 \ right )<0 $
定理
fを疑似凸関数とし、$ \ hat {x} \ in S $に対して$ \ bigtriangledown f \ left(\ hat {x} \ right)= 0 $とすると、$ \ hat {x} $はグローバル最適です。 S上のfの解。
証明
$ \ hat {x} $をfの臨界点とします。つまり、$ \ bigtriangledown f \ left(\ hat {x} \ right)= 0 $
fは疑似凸関数であるため、$ x \ in S、$の場合、次のようになります。
$$ \ bigtriangledown f \ left(\ hat {x} \ right)\ left(x- \ hat {x} \ right)= 0 \ Rightarrow f \ left(\ hat {x} \ right)\ leq f \ left (x \ right)、\ forall x \ in S $$
したがって、$ \ hat {x} $はグローバルな最適解です。
リマーク
fが厳密に疑似凸関数である場合、$ \ hat {x} $は一意のグローバル最適解です。
定理
fがSに対して微分可能な準凸関数である場合、fは厳密に準凸関数であると同時に準凸関数でもあります。
備考
$ \ mathbb {R} ^ n $の開集合Sで定義された2つの擬凸関数の合計は、擬凸ではない可能性があります。
$ f:S \ rightarrow \ mathbb {R} $を準凸関数、Sを$ \ mathbb {R} ^ n $の空でない凸部分集合とすると、すべての臨界点がグローバルである場合に限り、fは疑似凸です。 S上のfの最小値。
Sを$ \ mathbb {R} ^ n $の空でない凸部分集合とし、$ f:S \ rightarrow \ mathbb {R} $を$ \ bigtriangledown f \ left(x \ right)\ neqのような関数とします。 $ x \ in S $ごとに0 $の場合、fは準凸関数である場合に限り、疑似凸です。
凸計画問題には4つのタイプがあります-
Step 1 − $ min \:f \ left(x \ right)$、ここで$ x \ in S $とSは$ \ mathbb {R} ^ n $と$ f \ left(x \ right)の空でない凸集合です。 )$は凸関数です。
Step 2 − $ min \:f \ left(x \ right)、x \ in \ mathbb {R} ^ n $
$ g_i \ left(x \ right)\ geq 0、1 \ leq m_1 $および$ g_i \ left(x \ right)$は凸関数です。
$ g_i \ left(x \ right)\ leq 0、m_1 + 1 \ leq m_2 $および$ g_i \ left(x \ right)$は凹関数です。
$ g_i \ left(x \ right)= 0、m_2 + 1 \ leq m $および$ g_i \ left(x \ right)$は線形関数です。
ここで、$ f \ left(x \ right)$は凸関数です。
Step 3 − $ max \:f \ left(x \ right)$ここで、$ x \ in S $とSは$ \ mathbb {R} ^ n $と$ f \ left(x \ right)の空でない凸集合です。 $は凹関数です。
Step 4 − $ min \:f \ left(x \ right)$、ここで$ x \ in \ mathbb {R} ^ n $
$ g_i \ left(x \ right)\ geq 0、1 \ leq m_1 $および$ g_i \ left(x \ right)$は凸関数です。
$ g_i \ left(x \ right)\ leq 0、m_1 + 1 \ leq m_2 $および$ g_i \ left(x \ right)$は凹関数です。
$ g_i \ left(x \ right)= 0、m_2 + 1 \ leq m $および$ g_i \ left(x \ right)$は線形関数です。
ここで、$ f \ left(x \ right)$は凹関数です。
実行可能な方向のコーン
Sを$ \ mathbb {R} ^ n $の空でない集合とし、$ \ hat {x} \ in \:Closure \ left(S \ right)$とすると、$でのSの実行可能な方向の円錐Dで表される\ hat {x} $は、$ D = \ left \ {d:d \ neq 0、\ hat {x} + \ lambda d \ in S、\ lambda \ in \ left(0、 \ delta \ right)、\ delta> 0 \ right \} $
ゼロ以外の各ベクトル$ d \ in D $は、実行可能方向と呼ばれます。
与えられた関数$ f:\ mathbb {R} ^ n \ Rightarrow \ mathbb {R} $に対して、$ \ hat {x} $で方向を改善する円錐はFで表され、次の式で与えられます。
$$ F = \ left \ {d:f \ left(\ hat {x} + \ lambda d \ right)\ leq f \ left(\ hat {x} \ right)、\ forall \ lambda \ in \ left( 0、\ delta \ right)、\ delta> 0 \ right \} $$
$ d \ in F $の各方向は、$ \ hat {x} $でのfの改善方向または下降方向と呼ばれます。
定理
Necessary Condition
$ x \ in S $のような問題$ min f \ left(x \ right)$を考えてみましょう。ここで、Sは$ \ mathbb {R} ^ n $の空でない集合です。fが$ \ hat {x} \ in S $の点で微分可能であると仮定します。$ \ hat {x} $が局所最適解である場合、$ F_0 \ cap D = \ phi $ where $ F_0 = \ left \ {d:\ bigtriangledown f \ left(\ hat {x} \ right)^ T d <0 \ right \} $であり、Dは実行可能な方向の円錐です。
Sufficient Condition
$ F_0 \ cap D = \ phi $ fが$ \ hat {x} $の疑似凸関数であり、$ \ hat {x}、N_ \ varepsilon \ left(\ hat {x} \ right)の近傍が存在する場合、\ varepsilon> 0 $で、$ d = x- \ hat {x} \ in D $ for any $ x \ in S \ cap N_ \ varepsilon \ left(\ hat {x} \ right)$、次に$ \ hat {x} $は局所的な最適解です。
証明
Necessary Condition
$ F_0 \ cap D \ neq \ phi $とします。つまり、$ d \ in F_0 $と$ d \ in D $のような$ d \ in F_0 \ cap D $が存在します。
$ d \ in D $なので、$ \ hat {x} + \ lambda d \ in S、\ lambda \ in \ left(0、\ delta_1 \ right)。$のような$ \ delta_1> 0 $が存在します。
$ d \ in F_0 $なので、$ \ bigtriangledown f \ left(\ hat {x} \ right)^ T d <0 $
したがって、$ f \ left(\ hat {x} + \ lambda d \ right)<f \ left(\ hat {x} \ right)、\ forall \ lambda \ infのような$ \ delta_2> 0 $が存在します。 \ left(0、\ delta_2 \ right)$
$ \ delta = min \ left \ {\ delta_1、\ delta_2 \ right \} $とします
次に、$ \ hat {x} + \ lambda d \ in S、f \ left(\ hat {x} + \ lambda d \ right)<f \ left(\ hat {x} \ right)、\ forall \ lambda \ in f \ left(0、\ delta \ right)$
しかし、$ \ hat {x} $は局所的な最適解です。
したがって、それは矛盾です。
したがって、$ F_0 \ cap D = \ phi $
Sufficient Condition
$ F_0 \ cap D \ neq \ phi $ ndとし、fを疑似凸関数とします。
$ d = x- \ hat {x}、\ forall x \ in S \のような$ \ hat {x}、N _ {\ varepsilon} \ left(\ hat {x} \ right)$の近傍が存在するとします。キャップN_ \ varepsilon \ left(\ hat {x} \ right)$
$ \ hat {x} $が局所的な最適解ではないとします。
したがって、$ \ bar {x} \ in S \ cap N_ \ varepsilon \ left(\ hat {x} \ right)$が存在し、$ f \ left(\ bar {x} \ right)<f \ left( \ hat {x} \ right)$
$ S \ cap N_ \ varepsilon \ left(\ hat {x} \ right)、d = \ left(\ bar {x}-\ hat {x} \ right)\ in D $を仮定すると
fの擬凸性により、
$$ f \ left(\ hat {x} \ right)> f \ left(\ bar {x} \ right)\ Rightarrow \ bigtriangledown f \ left(\ hat {x} \ right)^ T \ left(\ bar {x}-\ hat {x} \ right)<0 $$
$ \ Rightarrow \ bigtriangledown f \ left(\ hat {x} \ right)^ T d <0 $
$ \ Rightarrow d \ in F_0 $
したがって、$ F_0 \ cap D \ neq \ phi $
これは矛盾です。
したがって、$ \ hat {x} $は局所最適解です。
次の問題を考えてみましょう。$ min \:f \ left(x \ right)$ここで、$ x \ in X $は、$ g_x \ left(x \ right)\ leq 0、i = 1,2、...、 m $
$ f:X \ rightarrow \ mathbb {R}、g_i:X \ rightarrow \ mathbb {R} ^ n $そしてXは$ \ mathbb {R} ^ n $の開集合です
$ S = \ left \ {x:g_i \ left(x \ right)\ leq 0、\ forall i \ right \} $とします。
$ \ hat {x} \ in X $とし、次に$ M = \ left \ {1,2、...、m \ right \} $
$ I = \ left \ {i:g_i \ left(\ hat {x} \ right)= 0、i \ in M \ right \} $とします。ここで、Iは$ \ hat {xのすべてのアクティブな制約のインデックスセットと呼ばれます。 } $
$ J = \ left \ {i:g_i \ left(\ hat {x} \ right)<0、i \ in M \ right \} $とします。ここで、Jは$ \ hat {xのすべてのアクティブな制約のインデックスセットと呼ばれます。 } $。
$ F_0 = \ left \ {d \ in \ mathbb {R} ^ m:\ bigtriangledown f \ left(\ hat {x} \ right)^ T d <0 \ right \} $
$ G_0 = \ left \ {d \ in \ mathbb {R} ^ m:\ bigtriangledown gI \ left(\ hat {x} \ right)^ T d <0 \ right \} $
または$ G_0 = \ left \ {d \ in \ mathbb {R} ^ m:\ bigtriangledown gi \ left(\ hat {x} \ right)^ T d <0、\ forall i \ in I \ right \} $
補題
$ S = \ left \ {x \ in X:g_i \ left(x \ right)\ leq 0、\ forall i \ in I \ right \} $であり、Xが$ \ mathbb {Rで空でない開集合である場合} ^ n $。$ \ hat {x} \ in S $と$ g_i $が$ \ hat {x}、i \ in I $で異なり、$ g_i $が$ i \ in J $が$ \ hat {xで連続であるとします。 } $、次に$ G_0 \ subseteq D $。
証明
$ d \ in G_0 $
$ \ hat {x} \ in X $であり、Xは開集合であるため、$ \ hat {x} + \ lambda d \ in X $ for $ \ lambda \ in \のような$ \ delta_1> 0 $が存在します。左(0、\ delta_1 \ right)$
また、$ g_ \ hat {x} <0 $と$ g_i $は$ \ hat {x}、\ forall i \ in J $で連続しているため、$ \ delta_2> 0 $、$ g_i \ left(\ hat {x} + \ lambda d \ right)<0、\ lambda \ in \ left(0、\ delta_2 \ right)$
したがって、$ d \ in G_0 $なので、$ \ bigtriangledown g_i \ left(\ hat {x} \ right)^ T d <0、\ forall i \ in I $したがって、$ \ delta_3> 0、g_i \ leftが存在します。 (\ hat {x} + \ lambda d \ right)<g_i \ left(\ hat {x} \ right)= 0 $、for $ \ lambda \ in \ left(0、\ delta_3 \ right)i \ in J $
$ \ delta = min \ left \ {\ delta_1、\ delta_2、\ delta_3 \ right \} $とします
したがって、$ \ hat {x} + \ lambda d \ in X、g_i \ left(\ hat {x} + \ lambda d \ right)<0、i \ in M $
$ \ Rightarrow \ hat {x} + \ lambda d \ in S $
$ \ Rightarrow d \ in D $
$ \ Rightarrow G_0 \ subseteq D $
したがって、証明されました。
定理
Necessary Condition
$ f $と$ g_i、i \ in I $が$ \ hat {x} \ in Sで異なり、$と$ g_j $が$ \ hat {x} \ in S $で連続しているとします。$ \ hat {x} $が$ S $の極小値である場合、$ F_0 \ cap G_0 = \ phi $。
Sufficient Condition
$ F_0 \ cap G_0 = \ phi $であり、fが$ \ left(\ hat {x}、g_i 9x \ right)の疑似凸関数である場合、i \ in I $はいくつかの$ \ varepsilon $上の疑似凸関数です-近傍$ \ hat {x}のうち、\ hat {x} $は局所的な最適解です。
備考
$ \ hat {x} $を、$ \ bigtriangledown f \ left(\ hat {x} \ right)= 0 $のように実行可能点とし、$ F_0 = \ phi $とします。したがって、$ F_0 \ cap G_0 = \ phi $ですが、$ \ hat {x} $は最適解ではありません
しかし、$ \ bigtriangledown g \ left(\ hat {x} \ right)= 0 $の場合、$ G_0 = \ phi $、したがって$ F_0 \ cap G_0 = \ phi $
問題を考えてみましょう:$ g \ left(x \ right)= 0 $となるようなmin $ f \ left(x \ right)$。
$ g \ left(x \ right)= 0 $なので、$ g_1 \ left(x \ right)= g \ left(x \ right)<0 $および$ g_2 \ left(x \ right)=-g \ left(x \ right)\ leq 0 $。
$ \ hat {x} \ in S $とし、次に$ g_1 \ left(\ hat {x} \ right)= 0 $および$ g_2 \ left(\ hat {x} \ right)= 0 $とします。
しかし、$ \ bigtriangledown g_1 \ left(\ hat {x} \ right)=-\ bigtriangledown g_2 \ left(\ hat {x} \ right)$
したがって、$ G_0 = \ phi $および$ F_0 \ cap G_0 = \ phi $です。
必要条件
定理
問題を考えてみましょう-$ min f \ left(x \ right)$このような$ x \ in X $ここで、Xは$ \ mathbb {R} ^ n $の開集合であり、$ g_i \ left(x \ right) \ leq 0、\ forall i = 1,2、.... m $。
$ f:X \ rightarrow \ mathbb {R} $と$ g_i:X \ rightarrow \ mathbb {R} $とします。
$ \ hat {x} $を実行可能解とし、fと$ g_i、i \ in I $を$ \ hat {x} $で微分可能とし$ g_i、i \ in J $を$ \ hat {で連続とします。 x} $。
$ \ hat {x} $が上記の問題をローカルで解決する場合、$ u_0、u_i \ in \ mathbb {R}、i \ in I $が存在し、$ u_0 \ bigtriangledown f \ left(\ hat {x} \ right)+ \ displaystyle \ sum \ Limits_ {i \ in I} u_i \ bigtriangledown g_i \ left(\ hat {x} \ right)$ = 0
ここで、$ u_0、u_i \ geq 0、i \ in I $および$ \ left(u_0、u_I \ right)\ neq \ left(0,0 \ right)$
さらに、$ g_i、i \ in J $も$ \ hat {x} $で微分可能である場合、上記の条件は次のように記述できます。
$ u_0 \ bigtriangledown f \ left(\ hat {x} \ right)+ \ displaystyle \ sum \ limits_ {i = 1} ^ m u_i \ bigtriangledown g_i \ left(\ hat {x} \ right)= 0 $
$ u_ig_i \ left(\ hat {x} \ right)$ = 0
$ u_0、u_i \ geq 0、\ forall i = 1,2、....、m $
$ \ left(u_0、u \ right)\ neq \ left(0,0 \ right)、u = \ left(u_1、u_2、s、u_m \ right)\ in \ mathbb {R} ^ m $
備考
$ u_i $はラグランジュ乗数と呼ばれます。
$ \ hat {x} $が特定の問題に対して実行可能であるという条件は、主要な実行可能条件と呼ばれます。
$ u_0 \ bigtriangledown f \ left(\ hat {x} \ right)+ \ displaystyle \ sum \ limits_ {i = 1} ^ m ui \ bigtriangledown g_i \ left(x \ right)= 0 $の要件はデュアル実現可能性と呼ばれます状態。
条件$ u_ig_i \ left(\ hat {x} \ right)= 0、i = 1、2、... m $は相補的たるみ条件と呼ばれます。この条件には$ u_i = 0、i \ in J $が必要です
主要な実行可能条件、二重の実行可能条件、および補完的なたるみを合わせて、フリッツ・ジョン条件と呼びます。
十分条件
定理
$ \ hat {x} N_ \ varepsilon \ left(\ hat {x} \ right)、\ varepsilon> 0 $の$ \ varepsilon $近傍が存在する場合、fは$ N_ \ varepsilon \ left( \ hat {x} \ right)\ cap S $と$ g_i、i \ in I $は、$ N_ \ varepsilon \ left(\ hat {x} \ right)\ cap S $、次に$ \ hat {上で厳密に擬凸です。 x} $は、上記の問題に対する局所的な最適解です。fが$ \ hat {x} $の擬凸であり、$ g_iの場合、i \ in I $は両方とも厳密に擬凸で$ \ hat {x}の準凸関数である場合、\ hat {x} $は問題のグローバルな最適解です。上記の。
例
$ min \:f \ left(x_1、x_2 \ right)= \ left(x_1-3 \ right)^ 2 + \ left(x_2-2 \ right)^ 2 $
$ x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 5、x_1 + 2x_2 \ leq 4、x_1、x_2 \ geq 0 $および$ \ hat {x} = \ left(2 、1 \ right)$
$ g_1 \ left(x_1、x_2 \ right)= x_ {1} ^ {2} + x_ {2} ^ {2} -5、$とします。
$ g_2 \ left(x_1、x_2 \ right)= x_1 + 2x_2-4、$
$ g_3 \ left(x_1、x_2 \ right)=-x_1 $および$ g_4 \ left(x_1、x_2 \ right)= -x_2 $。
したがって、上記の制約は次のように書くことができます。
$ g_1 \ left(x_1、x_2 \ right)\ leq 0、$
$ g_2 \ left(x_1、x_2 \ right)\ leq 0、$
$ g_3 \ left(x_1、x_2 \ right)\ leq 0 $および
$ g_4 \ left(x_1、x_2 \ right)\ leq 0 $したがって、$ I = \ left \ {1,2 \ right \} $したがって、$ u_3 = 0、u_4 = 0 $
$ \ bigtriangledown f \ left(\ hat {x} \ right)= \ left(2、-2 \ right)、\ bigtriangledown g_1 \ left(\ hat {x} \ right)= \ left(4,2 \ right )$および$ \ bigtriangledown g_2 \ left(\ hat {x} \ right)= \ left(1,2 \ right)$
したがって、これらの値をフリッツ・ジョン条件の最初の条件に入れると、次のようになります。
$ u_0 = \ frac {3} {2} u_2、\:\:u_1 = \ frac {1} {2} u_2、$そして$ u_2 = 1 $とすると、$ u_0 = \ frac {3} {2} 、\:\:u_1 = \ frac {1} {2} $
したがって、フリッツ・ジョンの条件が満たされます。
$ min f \ left(x_1、x_2 \ right)=-x_1 $。
$ x_2- \ left(1-x_1 \ right)^ 3 \ leq 0 $、
$ -x_2 \ leq 0 $および$ \ hat {x} = \ left(1,0 \ right)$
$ g_1 \ left(x_1、x_2 \ right)= x_2- \ left(1-x_1 \ right)^ 3 $、
$ g_2 \ left(x_1、x_2 \ right)=-x_2 $
したがって、上記の制約は次のように記述できます。
$ g_1 \ left(x_1、x_2 \ right)\ leq 0、$
$ g_2 \ left(x_1、x_2 \ right)\ leq 0、$
したがって、$ I = \ left \ {1,2 \ right \} $
$ \ bigtriangledown f \ left(\ hat {x} \ right)= \ left(-1,0 \ right)$
$ \ bigtriangledown g_1 \ left(\ hat {x} \ right)= \ left(0,1 \ right)$および$ g_2 \ left(\ hat {x} \ right)= \ left(0、-1 \ right )$
したがって、これらの値をフリッツ・ジョン条件の最初の条件に入れると、次のようになります。
$ u_0 = 0、\:\:u_1 = u_2 = a> 0 $
したがって、フリッツ・ジョンの条件が満たされます。
問題を考えてください-
$ min \:f \ left(x \ right)$このような$ x \ in X $、ここでXは$ \ mathbb {R} ^ n $と$ g_i \ left(x \ right)\ leqの開集合です0、i = 1、2、...、m $
$ S = \ left \ {x \ in X:g_i \ left(x \ right)\ leq 0、\ forall i \ right \} $とします。
$ \ hat {x} \ in S $とし、$ f $と$ g_i、i \ in I $を$ \ hat {x} $と$ g_iで微分可能とし、i \ in J $は$ \ hatで連続します。 {x} $。さらに、$ \ bigtriangledown g_i \ left(\ hat {x} \ right)、i \ in I $は線形独立です。$ \ hat {x} $が上記の問題をローカルで解決する場合、$ u_i、i \ in I $は次のように存在します。
$ \ bigtriangledown f \ left(x \ right)+ \ displaystyle \ sum \ limits_ {i \ in I} u_i \ bigtriangledown g_i \ left(\ hat {x} \ right)= 0 $、$ \:\:u_i \ geq 0、i \ in I $
$ g_i、i \ in J $も$ \ hat {x} $で微分可能である場合。次に$ \ hat {x} $、次に
$ \ bigtriangledown f \ left(\ hat {x} \ right)+ \ displaystyle \ sum \ limits_ {i = 1} ^ m u_i \ bigtriangledown g_i \ left(\ hat {x} \ right)= 0 $
$ u_ig_i \ left(\ hat {x} \ right)= 0、\ forall i = 1,2、...、m $
$ u_i \ geq 0 \ forall i = 1,2、...、m $
例
次の問題を考えてください-
$ min \:f \ left(x_1、x_2 \ right)= \ left(x_1-3 \ right)^ 2 + \ left(x_2-2 \ right)^ 2 $
$ x_ {1} ^ {2} + x_ {2} ^ {2} \ leq 5 $、
$ x_1,2x_2 \ geq 0 $および$ \ hat {x} = \ left(2,1 \ right)$
$ g_1 \ left(x_1、x_2 \ right)= x_ {1} ^ {2} + x_ {2} ^ {2} -5 $、
$ g_2 \ left(x_1、x_2 \ right)= x_ {1} + 2x_2-4 $
$ g_3 \ left(x_1、x_2 \ right)=-x_ {1} $および$ g_4 \ left(x_1、x_2 \ right)=-x_2 $
したがって、上記の制約は次のように書くことができます。
$ g_1 \ left(x_1、x_2 \ right)\ leq 0、g_2 \ left(x_1、x_2 \ right)\ leq 0 $
$ g_3 \ left(x_1、x_2 \ right)\ leq 0、$および$ g_4 \ left(x_1、x_2 \ right)\ leq 0 $したがって、$ I = \ left \ {1,2 \ right \} $ 、$ u_3 = 0、\:\:u_4 = 0 $
$ \ bigtriangledown f \ left(\ hat {x} \ right)= \ left(2、-2 \ right)、\ bigtriangledown g_1 \ left(\ hat {x} \ right)= \ left(4,2 \ right )$と
$ \ bigtriangledown g_2 \ left(\ hat {x} \ right)= \ left(1,2 \ right)$
したがって、これらの値をKarush-Kuhn-Tucker条件の最初の条件に入れると、次のようになります。
$ u_1 = \ frac {1} {3} $および$ u_2 = \ frac {2} {3} $
したがって、Karush-Kuhn-Tucker条件が満たされます。
最急降下の方法
この方法は、勾配法またはコーシー法とも呼ばれます。この方法には、次の用語が含まれます-
$$ x_ {k + 1} = x_k + \ alpha_kd_k $$
$ d_k =-\ bigtriangledown f \ left(x_k \ right)$または$ d_k =-\ frac {\ bigtriangledown f \ left(x_k \ right)} {\ left \ | \ bigtriangledown f \ left(x_k \ right)\ right \ |} $
$ \ phi \ left(\ alpha \ right)= f \ left(x_k + \ alpha d_k \ right)$とします。
$ \ phi $を微分してゼロに等しくすることにより、$ \ alpha $を取得できます。
したがって、アルゴリズムは次のようになります-
$ x_0 $、$ \ varepsilon_1 $、$ \ varepsilon_2 $を初期化し、$ k = 0 $に設定します。
$ d_k =-\ bigtriangledown f \ left(x_k \ right)$または$ d_k =-\ frac {\ bigtriangledown f \ left(x_k \ right)} {\ left \ | \ bigtriangledown f \ left(x_k \ right)を設定します\ right \ |} $。
$ \ phi \ left(\ alpha \ right)= f \ left(x_k + \ alpha d_k \ right)$を最小化するように$ \ alpha_k $を見つけます。
$ x_ {k + 1} = x_k + \ alpha_kd_k $を設定します。
$ \ left \ |の場合 x_ {k + 1-x_k} \ right \ | <\ varepsilon_1 $または$ \ left \ | \ bigtriangledown f \ left(x_ {k + 1} \ right)\ right \ | \ leq \ varepsilon_2 $、ステップ6に進みます。それ以外の場合は、$ k = k + 1 $を設定して、ステップ2に進みます。
最適なソリューションは$ \ hat {x} = x_ {k + 1} $です。
ニュートン法
ニュートン法は次の原理で機能します-
$ f \ left(x \ right)= y \ left(x \ right)= f \ left(x_k \ right)+ \ left(x-x_k \ right)^ T \ bigtriangledown f \ left(x_k \ right)+ \ frac {1} {2} \ left(x-x_k \ right)^ TH \ left(x_k \ right)\ left(x-x_k \ right)$
$ \ bigtriangledown y \ left(x \ right)= \ bigtriangledown f \ left(x_k \ right)+ H \ left(x_k \ right)\ left(x-x_k \ right)$
$ x_ {k + 1}で、\ bigtriangledown y \ left(x_ {k + 1} \ right)= \ bigtriangledown f \ left(x_k \ right)+ H \ left(x_k \ right)\ left(x_ {k +1} -x_k \ right)$
$ x_ {k + 1} $が最適解であるために$ \ bigtriangledown y \ left(x_k + 1 \ right)= 0 $
したがって、$ x_ {k + 1} = x_k-H \ left(x_k \ right)^ {-1} \ bigtriangledown f \ left(x_k \ right)$
ここで、$ H \ left(x_k \ right)$は特異ではないはずです。
したがって、アルゴリズムは次のようになります-
Step 1 − $ x_0、\ varepsilon $を初期化し、$ k = 0 $を設定します。
Step 2 − $ H \ left(x_k \ right)\ bigtriangledown f \ left(x_k \ right)$を見つけます。
Step 3 −線形システム$ H \ left(x_k \ right)h \ left(x_k \ right)= \ bigtriangledown f \ left(x_k \ right)$を$ h \ left(x_k \ right)$について解きます。
Step 4 − $ x_ {k + 1} = x_k-h \ left(x_k \ right)$を見つけます。
Step 5− $ \ left \ |の場合 x_ {k + 1} -x_k \ right \ | <\ varepsilon $または$ \ left \ | \ bigtriangledown f \ left(x_k \ right)\ right \ | \ leq \ varepsilon $次にステップ6に進みます。それ以外の場合は、$ k = k + 1 $を設定して、ステップ2に進みます。
Step 6 −最適解は$ \ hat {x} = x_ {k + 1} $です。
共役勾配法
この方法は、次のタイプの問題を解決するために使用されます-
$ min f \ left(x \ right)= \ frac {1} {2} x ^ T Qx-bx $
ここで、Qは正定値のnXn行列で、bは定数です。
$ x_0、\ varepsilon、$が与えられると、$ g_0 = Qx_0-b $を計算します
$ k = 0,1,2、...、$に$ d_0 = -g_0 $を設定します
$ \ alpha_k = \ frac {g_ {k} ^ {T} g_k} {d_ {k} ^ {T} Q d_k} $を設定します
$ x_ {k + 1} = x_k + \ alpha_kd_k $を計算します
$ g_ {k + 1} = g_k + \ alpha_kd_k $を設定します
$ \ beta_k = \ frac {g_ {k} ^ {T} g_k} {d_ {k} ^ {T} Qd_k} $を計算します
$ x_ {k + 1} = x_k + \ alpha_kd_k $を計算します
$ g_ {k + 1} = x_k + \ alpha_kQd_k $を設定します
$ \ beta_k = \ frac {g_ {k + 1} ^ {T} g_ {k + 1}} {g_ {k} ^ {T} gk} $を計算します
$ d_ {k + 1} = -g_ {k + 1} + \ beta_kd_k $を設定します。