Kosmologia - odległość średnicy kątowej
W tym rozdziale zrozumiemy, czym jest odległość w średnicy kątowej i jak pomaga w kosmologii.
Dla obecnego wszechświata -
$ \ Omega_ {m, 0} \: = \: 0,3 $
$ \ Omega _ {\ wedge, 0} \: = \: 0,69 $
$ \ Omega_ {rad, 0} \: = \: 0,01 $
$ \ Omega_ {k, 0} \: = \: 0 $
Do tej pory badaliśmy dwa rodzaje odległości -
Proper distance (lp) - Odległość, jaką pokonują fotony od źródła do nas, tj Instantaneous distance.
Comoving distance (lc) - Odległość między obiektami w przestrzeni, która się nie rozszerza, tj. distance in a comoving frame of reference.
Odległość jako funkcja przesunięcia ku czerwieni
Rozważmy galaktykę, która w danym momencie promieniuje fotonem t1 który jest wykrywany przez obserwatora o godz t0. Możemy zapisać odpowiednią odległość do galaktyki jako -
$$ l_p = \ int_ {t_1} ^ {t_0} cdt $$
Niech nastąpi przesunięcie ku czerwieni galaktyki z,
$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {1} {a ^ 2} \ frac {\ mathrm {d} a} {\ mathrm {d} t} $$
$$ \ Rightarrow \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {\ frac {\ mathrm {d} a} {\ mathrm {d} t}} {a} \ frac {1} {a} $$
$$ \ Dlatego \ frac {\ mathrm {d} z} {\ mathrm {d} t} = - \ frac {H (z)} {a} $$
Teraz zbliżająca się odległość galaktyki w dowolnym momencie t będzie -
$$ l_c = \ frac {l_p} {a (t)} $$
$$ l_c = \ int_ {t_1} ^ {t_0} \ frac {cdt} {a (t)} $$
Jeśli chodzi o z,
$$ l_c = \ int_ {t_0} ^ {t_1} \ frac {cdz} {H (z)} $$
Istnieją dwa sposoby znajdowania odległości, które są następujące:
Zależność strumień-jasność
$$ F = \ frac {L} {4 \ pi d ^ 2} $$
gdzie d to odległość u źródła.
Odległość średnicy kątowej źródła
Jeśli znamy rozmiar źródła, jego szerokość kątowa wskaże nam odległość od obserwatora.
$$ \ theta = \ frac {D} {l} $$
gdzie l jest odległością średnicy kątowej źródła.
θ to rozmiar kątowy źródła.
D to rozmiar źródła.
Rozważmy galaktykę o rozmiarze D i rozmiarze kątowym dθ.
Wiemy to,
$$ d \ theta = \ frac {D} {d_A} $$
$$ \ więc D ^ 2 = a (t) ^ 2 (r ^ 2 d \ theta ^ 2) \ quad \ ponieważ dr ^ 2 = 0; \: d \ phi ^ 2 \ około 0 $$
$$ \ Rightarrow D = a (t) rd \ theta $$
Wymiana pieniędzy r do rc, zbliżająca się odległość galaktyki, mamy -
$$ d \ theta = \ frac {D} {r_ca (t)} $$
Tutaj, jeśli wybierzemy t = t0kończymy na pomiarze obecnej odległości do galaktyki. AleDjest mierzona w momencie emisji fotonu. Dlatego przy użyciut = t0uzyskujemy większą odległość do galaktyki, a tym samym niedoszacowanie jej wielkości. Dlatego powinniśmy wykorzystać czast1.
$$ \ dlatego d \ theta = \ frac {D} {r_ca (t_1)} $$
Porównując to z poprzednim wynikiem, otrzymujemy -
$$ d_ \ wedge = a (t_1) r_c $$
$$ r_c = l_c = \ frac {d_ \ wedge} {a (t_1)} = d_ \ wedge (1 + z_1) \ quad \ ponieważ 1 + z_1 = \ frac {1} {a (t_1)} $$
W związku z tym,
$$ d_ \ wedge = \ frac {c} {1 + z_1} \ int_ {0} ^ {z_1} \ frac {dz} {H (z)} $$
dA to odległość średnicy kątowej obiektu.
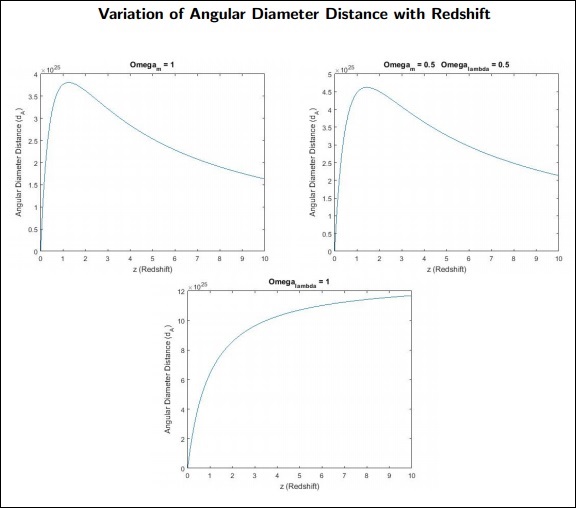
Punkty do zapamiętania
Jeśli znamy rozmiar źródła, jego szerokość kątowa wskaże nam odległość od obserwatora.
Właściwa odległość to odległość, jaką pokonują fotony od źródła do nas.
Dystans w ruchu to odległość między obiektami w przestrzeni, która się nie rozszerza.