Kosmologia - szybki przewodnik

Cosmologyto badanie wszechświata. W tamtych czasach istniało kilka szkół myśli dotyczących pochodzenia wszechświata. Wielu uczonych wierzyło wSteady State Theory. Zgodnie z tą teorią wszechświat był zawsze ten sam, nie miał początku.

Chociaż była grupa ludzi, którzy wierzyli w Big Bang Theory. Ta teoria przewiduje początek wszechświata. Były dowody na gorące pozostawione promieniowanie z Wielkiego Wybuchu, które ponownie potwierdza model. Teoria Wielkiego Wybuchu przewiduje obfitość lekkich pierwiastków we wszechświecie. Tak więc, idąc za słynnym modelem Wielkiego Wybuchu, możemy stwierdzić, że wszechświat miał początek. Żyjemy w rozszerzającym się wszechświecie.

Przesunięcie ku czerwieni Hubble'a

We wczesnych latach XX wieku najnowocześniejszy teleskop Mt Wilson, 100-calowy teleskop, był wówczas największym teleskopem. Hubble był jednym z wybitnych naukowców, którzy pracowali z tym teleskopem. Odkrył, że poza Drogą Mleczną istnieją galaktyki.Extragalactic Astronomyma zaledwie 100 lat. Mt Wilson był największym teleskopem do czasu zbudowania Obserwatorium Palmera, które miało 200-calowy teleskop.

Hubblenie był jedyną osobą obserwującą galaktyki poza Drogą Mleczną, pomógł mu Humason. Zaczęli mierzyć widma pobliskich galaktyk. Następnie zaobserwowali, że widmo galaktyczne znajdowało się w widzialnym zakresie długości fal z ciągłą emisją. Na szczycie kontinuum znajdowały się linie emisji i absorpcji. Na podstawie tych linii możemy oszacować, czy galaktyka oddala się od nas, czy do nas.

Kiedy otrzymujemy widmo, zakładamy, że pochodzi z najsilniejszej linii H-α. Z literatury najsilniejsza linia powinna występować na6563 Å, ale jeśli linia występuje gdzieś w pobliżu 7000Å, możemy łatwo powiedzieć, że jest przesunięty ku czerwieni.

Z Special Theory of Relativity,

$$1 + z = \sqrt{\frac{1+\frac{v}{c}}{1-\frac{v}{c}}}$$

gdzie Z jest przesunięciem ku czerwieni, liczbą bezwymiarową, av jest prędkością recesji.

$$\frac{\lambda_{obs}}{\lambda_{rest}} = 1 + z$$

Hubble i Humason zapisali się na liście 22 Galaxiesw swoim artykule. Prawie wszystkie te galaktyki wykazywały przesunięcie ku czerwieni. Wykreślili prędkość (km / s) w funkcji odległości (Mpc). Zaobserwowali liniowy trend i Hubble przedstawił swoje słynne prawo w następujący sposób.

$$v_r = H_o d$$

To jest Hubble Redshift Distance Relationship. Indeks dolnyrwskazuje, że ekspansja jest w kierunku promieniowym. Podczas,$v_r$ jest malejącą prędkością, $H_o$ jest parametrem Hubble'a, dto odległość galaktyki od nas. Doszli do wniosku, że odległe galaktyki oddalają się od nas szybciej, jeśli tempo rozszerzania się wszechświata jest jednolite.

Ekspansja

Wszystko się od nas oddala. Galaktyki nie są stacjonarne, zawsze występuje jakaś harmoniczna ekspansji. Jednostki parametru Hubble to km sec ⁻¹ Mpc ⁻¹ . Gdyby wyjść na odległość - 1 Mpc, galaktyki poruszałyby się z prędkością 200 km / s. Parametr Hubble'a podaje nam tempo ekspansji. Według Hubble'a i Humason'a, wartość$H_o$ wynosi 200 km / s / Mpc.

Dane pokazały, że wszystkie galaktyki oddalają się od nas. Zatem jest oczywiste, że znajdujemy się w centrum wszechświata. Ale Hubble nie popełnił tego błędu, według niego, w dowolnej galaktyce, w której żyjemy, wszystkie inne galaktyki oddalałyby się od nas. Zatem wniosek jest taki, że przestrzeń między galaktykami rozszerza się i nie ma centrum Wszechświata.

Ekspansja dzieje się wszędzie. Jednak są siły, które sprzeciwiają się ekspansji. Wiązania chemiczne, siła grawitacji i inne siły przyciągania trzymają obiekty razem. Wcześniej wszystkie obiekty były blisko siebie. Biorąc pod uwagę Wielki Wybuch jako siłę impulsową, obiekty te będą się oddalać od siebie.

Skala czasu

W skali lokalnej Kinematyka rządzi się grawitacją. W pierwotnym prawie Hubble'a istniało kilka galaktyk, które wykazywały przesunięcie w kierunku niebieskim. Można to przypisać połączonemu potencjałowi grawitacyjnemu galaktyk. Grawitacja oddzieliła rzeczy od prawa Hubble'a. Galaktyka Andromedy zbliża się do nas. Grawitacja próbuje spowolnić. Początkowo ekspansja zwalniała, teraz przyspiesza.

To było Cosmic Jerkz tego powodu. Dokonano kilku oszacowań parametru Hubble'a. Przez 90 lat ewoluował od 500 km / s / Mpc do 69 km / s / Mpc. Rozbieżność w wartości wynikała z niedoszacowania odległości. PlikCepheid Stars były używane jako kalibratory odległości, jednak istnieją różne typy gwiazd cefeid i fakt ten nie był brany pod uwagę przy szacowaniu parametru Hubble'a.

Czas Hubble'a

Stała Hubble'a daje nam realistyczne oszacowanie wieku Wszechświata. Plik$H_o$dałoby wiek Wszechświata pod warunkiem, że galaktyki poruszałyby się z tą samą prędkością. Odwrotność$H_o$ daje nam czas Hubble'a.

$$t_H = \frac{1}{H_o}$$

Zastąpienie obecnej wartości $H_o, t_H$ = 14miliard lat. Tempo ekspansji było stałe na początku Wszechświata. Nawet jeśli to nieprawda,$H_o$daje użyteczną granicę wieku Wszechświata. Zakładając stałą szybkość rozszerzania, kiedy wykreślamy wykres między odległością a czasem, nachylenie wykresu jest określone przez prędkość.

W tym przypadku czas Hubble'a jest równy czasowi rzeczywistemu. Jeśli jednak wszechświat rozszerzał się szybciej w przeszłości i wolniej w teraźniejszości, czas Hubble'a wyznacza górną granicę wieku Wszechświata. Jeśli wcześniej wszechświat rozszerzał się powoli, a teraz przyspiesza, to czas Hubble'a da dolną granicę wieku wszechświata.

• $t_H = t_{age}$ - jeśli szybkość ekspansji jest stała.

• $t_H > t_{age}$ - jeśli wszechświat rozszerzał się szybciej w przeszłości i wolniej w teraźniejszości.

• $t_H < t_{age}$ - jeśli wszechświat rozszerzał się wolniej w przeszłości i szybciej w teraźniejszości.

Rozważ grupę 10 galaktyk, które znajdują się w odległości 200 Mpc od innej grupy galaktyk. Galaktyki w gromadzie nigdy nie dochodzą do wniosku, że wszechświat się rozszerza, ponieważ kinematyka w lokalnej grupie jest rządzona grawitacją.

Punkty do zapamiętania

• Kosmologia to nauka o przeszłości, teraźniejszości i przyszłości naszego Wszechświata.

• Nasz wszechświat ma około 14 miliardów lat.

• Wszechświat stale się rozszerza.

• Parametr Hubble'a jest miarą wieku Wszechświata.

• Bieżąca wartość H_o wynosi 69 km / s / Mpc.

Przez bardzo długi czas nikt nie uważał, że galaktyki znajdują się poza naszą Drogą Mleczną. W 1924 roku wykrył Edwin HubbleCepheid’sw Mgławicy Andromedy i oszacował ich odległość. Doszedł do wniosku, że te „mgławice spiralne” były w rzeczywistości innymi galaktykami, a nie częścią naszej Drogi Mlecznej. Dlatego ustalił, że M31 (Galaktyka Andromedy) jest Wszechświatem Wyspowym. To były narodzinyExtragalactic Astronomy.

Program Cefeidy a periodic dip in their brightness. Z obserwacji wynika, że ​​okres między kolejnymi zapadkami zwany okresem pulsacji jest powiązany z jasnością. Mogą więc służyć jako wskaźniki odległości. Gwiazdy ciągu głównego, takie jak Słońce, znajdują się w równowadze hydrostatycznej i spalają wodór w swoim jądrze. Po całkowitym spaleniu wodoru gwiazdy zbliżają się do fazy czerwonego olbrzyma i próbują odzyskać równowagę.

Gwiazdy cefeidy są gwiazdami po głównym ciągu, które przechodzą z gwiazd głównego ciągu do czerwonych olbrzymów.

Klasyfikacja cefeid

Istnieją 3 szerokie klasy tych pulsujących gwiazd zmiennych -

• Type-I Cepheids (lub klasyczne cefeidy) - okres 30-100 dni.

• Type-II Cepheids (lub W Virginis Stars) - okres 1-50 dni.

• RR Lyrae Stars - okres 0,1-1 dnia.

W tym czasie Hubble nie był świadomy takiej klasyfikacji gwiazd zmiennych. Dlatego też doszło do przeszacowania stałej Hubble'a, z powodu którego oszacował niższy wiek naszego wszechświata. Dlatego też przeszacowano prędkość recesji. W cefeidach zaburzenia rozprzestrzeniają się promieniście na zewnątrz od środka gwiazdy, aż do osiągnięcia nowej równowagi.

Zależność między jasnością a okresem pulsacji

Spróbujmy teraz zrozumieć fizyczne podstawy faktu, że wyższy okres pulsacji oznacza większą jasność. Rozważmy gwiazdę o jasności L i masie M.

Wiemy, że -

$$L \propto M^\alpha$$

gdzie α = 3 do 4 dla gwiazd o małej masie.

Z Stefan Boltzmann Lawwiemy, że -

$$L \propto R^2 T^4$$

Gdyby R jest promieniem i $c_s$ to prędkość dźwięku, a następnie okres pulsacji P można zapisać jako -

$$P = R/c_s$$

Ale prędkość dźwięku przez dowolne medium można wyrazić w kategoriach temperatury jako -

$$c_s = \sqrt{\frac{\gamma P}{\rho}}$$

Tutaj, γ wynosi 1 dla przypadków izotermicznych.

Dla gazu doskonałego P = nkT, gdzie k to Boltzmann Constant. Więc możemy napisać -

$$P = \frac{\rho kT}{m}$$

gdzie $\rho$ jest gęstością i m jest masą protonu.

Dlatego okres jest określony przez -

$$P \cong \frac{Rm^{\frac{1}{2}}}{(kT)^{{\frac{1}{2}}}}$$

Virial Theorem stwierdza, że ​​dla stabilnego, samograwitującego, sferycznego rozkładu obiektów o jednakowej masie (takich jak gwiazdy, galaktyki), całkowita energia kinetyczna k obiektu jest równa minus połowa całkowitej energii potencjalnej grawitacji utj.

$$u = -2k$$

Załóżmy, że twierdzenie o wirusach jest prawdziwe dla tych gwiazd zmiennych. Jeśli weźmiemy pod uwagę proton znajdujący się bezpośrednio na powierzchni gwiazdy, to z twierdzenia o wirusie możemy powiedzieć -

$$\frac{GMm}{R} = mv^2$$

Z dystrybucji Maxwell,

$$v = \sqrt{\frac{3kT}{2}}$$

Dlatego okres -

$$P \sim \frac{RR^{\frac{1}{2}}}{(GM)^{\frac{1}{2}}}$$

co oznacza

$$P \propto \frac{R^{\frac{3}{2}}}{M^{\frac{1}{2}}}$$

Wiemy to - $M \propto L^{1/\alpha}$

Również $R \propto L^{1/2}$

Więc dla β > 0w końcu otrzymujemy - $P \propto L^\beta$

Punkty do zapamiętania

• Gwiazdy cefeidy są gwiazdami po głównym ciągu, które przechodzą z gwiazd głównego ciągu do czerwonych olbrzymów.

• Cefeidy dzielą się na 3 typy: Typ I, Typ II, RR-Lyrae w kolejności malejącej pulsacji.

• Okres pulsowania cefeidy jest wprost proporcjonalny do jej jasności (jasności).

Obserwacje Hubble'a wykorzystywały fakt, że prędkość radialna jest powiązana z przesunięciem Spectral Lines. Tutaj będziemy obserwować cztery przypadki i znaleźć związek między prędkością recesyjną ($v_r$) i przesunięcie ku czerwieni (z).

Przypadek 1: Nierelatywistyczny przypadek ruchu Źródła

W tym przypadku v jest znacznie mniejsze niż c. Źródło emituje jakiś sygnał (dźwięk, światło itp.), Który rozchodzi się jakoWavefronts. Odstęp czasu między wysłaniem dwóch kolejnych sygnałów w ramce źródłowej wynosiΔts. Odstęp czasu między odbiorem dwóch kolejnych sygnałów w ramce obserwatora wynosiΔto.

Jeśli zarówno obserwator, jak i źródło są nieruchome, wówczas Δts = Δto, ale tak nie jest w tym przypadku. Zamiast tego relacja jest następująca.

$$\Delta t_o = \Delta t_s + \frac{\Delta l}{c}$$

Teraz, $\Delta l = v \Delta t_s$

Ponadto, ponieważ (prędkość fali x czas) = ​​długość fali, otrzymujemy

$$\frac{\Delta t_o}{\Delta t_s} = \frac{\lambda_o}{\lambda_s}$$

Z powyższych równań otrzymujemy następującą zależność -

$$\frac{\lambda_o}{\lambda_s} = 1 + \frac{v}{c}$$

gdzie $\lambda _s$ jest długością fali sygnału u źródła i $\lambda _o$ jest długością fali sygnału zinterpretowaną przez obserwatora.

Tutaj, ponieważ źródło oddala się od obserwatora, v jest pozytywna.

Przesunięcie ku czerwieni -

$$z = \frac{\lambda_o - \lambda_s}{\lambda_s} = \frac{\lambda_o}{\lambda_s} - 1$$

Z powyższych równań otrzymujemy przesunięcie ku czerwieni w następujący sposób.

$$z = \frac{v}{c}$$

Przypadek 2: nierelatywistyczny przypadek poruszania się obserwatora

W tym przypadku v jest znacznie mniejsze niż c. Tutaj,$\Delta l$ jest inny.

$$\Delta l = v \Delta t_o$$

Po uproszczeniu otrzymujemy -

$$\frac{\Delta t_o}{\Delta t_s} = \left ( 1 - \frac{v}{c} \right )^{-1}$$

Otrzymujemy przesunięcie ku czerwieni w następujący sposób -

$$z = \frac{v/c}{1-v/c}$$

Od v << c, wyrażenie przesunięcia ku czerwieni dla przypadku I i przypadku II jest w przybliżeniu takie samo.

Zobaczmy, jak różnią się przesunięcia czerwieni uzyskane w powyższych dwóch przypadkach.

$$z_{II} - z_I = \frac{v}{c} \left [ \frac{1}{1 - v/c}-1 \right ]$$

W związku z tym, $z_{II} − z_{I}$ to bardzo mała liczba ze względu na rozszerzenie $(v/c)^2$ czynnik.

Oznacza to, że jeśli v << c, nie możemy stwierdzić, czy źródło się porusza, czy też obserwator się porusza.

Rozumiemy teraz Basics of STR (Szczególna Teoria Względności) -

• Prędkość światła jest stała.

• Kiedy źródło (lub obserwator) porusza się z prędkością porównywalną do prędkości światła, obserwuje się efekty relatywistyczne.

• Dylatacja czasu: $\Delta t_o = \gamma \Delta t_s$

• Skurcz długości: $\Delta l_o = \Delta t_s/\gamma$

• Tutaj, $\gamma$ jest Lorrentz factorwiększe niż 1.

$$\gamma = \frac{1}{\sqrt{1-(v^2/c^2)}}$$

Przypadek 3: Relatywistyczny przypadek ruchu źródła

W tym przypadku v jest porównywalne z c. Odnieś się do tej samej figury, co w przypadku I. Ze względu na efekt relatywistyczny obserwuje się dylatację czasu, a zatem uzyskuje się następującą zależność. (Źródło porusza się z relatywistyczną prędkością)

$$\Delta t_o = \gamma \Delta t_s + \frac{\Delta l}{c}$$

$$\Delta l = \frac{v\gamma \Delta t_s}{c}$$

$$\frac{\Delta t_o}{\Delta t_s} = \frac{1 + v/c}{\sqrt{1- (v^2/c^2)}}$$

Przy dalszym uproszczeniu otrzymujemy:

$$1 + z = \sqrt{\frac{1+v/c}{1-v/c}}$$

Powyższe wyrażenie jest znane jako Kinematic Doppler Shift Expression.

Przypadek 4: Relatywistyczny przypadek poruszania się obserwatora

Zobacz ten sam rysunek, co w przypadku II. Ze względu na efekt relatywistyczny obserwuje się skrócenie czasu, dzięki czemu uzyskuje się następującą zależność. (Obserwator porusza się z relatywistyczną prędkością)

$$\Delta t_o = \frac{\Delta t_s}{\gamma}+\frac{\Delta l}{c}$$

$$\Delta l = \frac{v\Delta t_o}{c}$$

$$\frac{\Delta t_o}{\Delta t_s} = \frac{\sqrt{1-( v^2/c^2)}}{1-v/c}$$

Przy dalszym uproszczeniu otrzymujemy -

$$1 + z = \sqrt{\frac{1+ v/c}{1- v/c}}$$

Powyższe wyrażenie jest takie samo, jak to, co otrzymaliśmy dla przypadku III.

Punkty do zapamiętania

• Prędkość recesyjna i przesunięcie ku czerwieni gwiazdy to wielkości powiązane.

• W przypadku nierelatywistycznym nie możemy określić, czy źródło jest ruchome czy stacjonarne.

• W przypadku relatywistycznym nie ma różnicy w relacji prędkości przesunięcia ku czerwieni-recesji dla poruszającego się źródła lub obserwatora.

• Poruszające się zegary poruszają się wolniej, jest bezpośrednim wynikiem teorii względności.

Galaktyka z przesunięciem ku czerwieni z = 10, koresponduje z v≈80% z c. Wokół jest masa Drogi Mlecznej1011M⊙jeśli weźmiemy pod uwagę ciemną materię, to jest 1012M⊙. Nasza droga mleczna jest więc ogromna. Jeśli porusza się o 80%c, nie pasuje to do ogólnej koncepcji ruchu obiektów.

Wiemy,

$$\frac{v_r}{c} = \frac{\lambda_{obs} - \lambda{rest}}{\lambda_{rest}}$$

Dla małych wartości z,

$$z = \frac{v_r}{c} = \frac{\lambda_{obs}-\lambda_{rest}}{\lambda_{rest}}$$

Na poniższym wykresie, w klasie między strumieniem a długością fali, na szczycie kontinuum znajdują się linie emisji. ZH-α informacji o liniach, z grubsza możemy to stwierdzić z = 7. Oznacza to, że galaktyka porusza się w 70%c. Obserwujemy przesunięcie i interpretujemy je jako prędkość. Powinniśmy pozbyć się tego pojęcia i przyjrzeć sięzw inny sposób. Wyobraź sobie przestrzeń jako siatkę 2D reprezentującą wszechświat, jak pokazano poniżej.

Uznaj czarną gwiazdę za naszą własną drogę mleczną, a niebieską za jakąś inną galaktykę. Kiedy rejestrujemy światło z tej galaktyki, widzimy widmo i odkrywamy jego przesunięcie ku czerwieni, tj. Galaktyka oddala się. Wyemitowany foton miał względną prędkość.

• A co jeśli przestrzeń się poszerza?

• Jest to natychmiastowe przesunięcie fotonu ku czerwieni. Skumulowane przesunięcie ku czerwieni wzdłuż przestrzeni między dwiema galaktykami będzie miało tendencję do dużego przesunięcia ku czerwieni. W końcu długość fali się zmieni. Jest to raczej ekspansja przestrzeni niż ruch kinematyczny galaktyk.

Poniższy obraz pokazuje, że jeśli wzajemna grawitacja przepłynie przez ekspansję, to nie uczestniczy w prawie Hubble'a.

W kinematycznym przesunięciu dopplerowskim, przesunięcie ku czerwieni jest indukowane w fotonie w momencie emisji. W kosmologicznym przesunięciu ku czerwieni na każdym kroku następuje kumulatywne przesunięcie ku czerwieni. W potencjale grawitacyjnym foton zostanie przesunięty na niebiesko. Gdy wychodzi z potencjału grawitacyjnego, zostaje przesunięty ku czerwieni.

Zgodnie ze Szczególną Teorią Względności, dwa obiekty mijające się nie mogą mieć względnej prędkości większej niż prędkość światła. Prędkość, o której mówimy, dotyczy rozszerzania się wszechświata. W przypadku dużych wartości z przesunięcie ku czerwieni jest kosmologiczne i nie jest prawidłową miarą rzeczywistej prędkości recesji obiektu względem nas.

Zasada kosmologiczna

Wynika z Copernicus NotionWszechświata. Zgodnie z tym pojęciem wszechświat jest jednorodny i izotropowy. Nie ma preferowanego kierunku i lokalizacji we wszechświecie.

• Jednorodność oznacza, że ​​bez względu na to, w której części wszechświata przebywasz, zobaczysz, że wszechświat jest taki sam we wszystkich częściach. Natura izotropowa oznacza, że ​​bez względu na to, w którym kierunku spojrzysz, zobaczysz tę samą strukturę.

• Dobrym przykładem jednorodności jest pole ryżowe. Wygląda na jednorodną ze wszystkich stron, ale gdy płynie wiatr, występują różnice w jego orientacji, więc nie jest izotropowy. Rozważmy górę na płaskim terenie, a na szczycie stoi obserwator. Zobaczy izotropowy charakter płaskiego terenu, ale nie jest on jednorodny. Jeśli w jednorodnym wszechświecie jest izotropowy w pewnym punkcie, to jest izotropowy wszędzie.

• Przeprowadzono badania na dużą skalę w celu sporządzenia mapy wszechświata. Sloan Digital Sky Surveyjest jednym z takich badań, które nie skupiało się zbytnio na deklinacji, ale na rektascensji. Okres ważności wynosi około 2 miliardy lat. Każdy piksel odpowiada położeniu galaktyki, a kolor odpowiada strukturze morfologicznej. Zielony kolor reprezentował niebieską galaktykę spiralną, a czerwony fałszywy kolor oznaczał masywne galaktyki.

• Galaktyki znajdują się we włóknistej strukturze w kosmologicznej sieci, a między nimi są puste przestrzenie.

• $\delta M/M \cong 1$tzn. fluktuacja rozkładu masy wynosi 1 M to masa materii obecnej w danym sześcianie. W takim przypadku weź kostkę o objętości 50 Mpc.

• Dla boku sześcianu 1000 Mpc, $\delta M/M \cong 10^{−4}$.

• Jednym ze sposobów ilościowego określenia jednorodności jest analiza fluktuacji masy. Wahania masy będą większe w niższych skalach.

• Aby określić ilościowo charakter izotropowy, rozważ kosmiczne mikrofalowe promieniowanie tła. Wszechświat jest prawie izotropowy w dużych skalach kątowych.

Punkty do zapamiętania

• Dwa mijające się obiekty nie mogą mieć względnej prędkości większej niż prędkość światła.

• Zasada kosmologiczna stwierdza, że ​​wszechświat jest jednorodny i izotropowy.

• Ta jednorodność występuje w bardzo dużej skali kątowej, a nie w mniejszych skalach.

• SDSS (Sloan Digital Sky Survey) to próba mapowania nocnego nieba, weryfikująca zasadę kosmologii.

Zgodnie z prawem zachowania energii i prawem zachowania masy, całkowita ilość energii łącznie z masą (E = mc ² ) pozostaje niezmieniona na każdym etapie dowolnego procesu we wszechświecie. Sama ekspansja Wszechświata pochłania energię, która może pochodzić z rozciągania długości fal fotonów (kosmologiczne przesunięcie ku czerwieni), interakcji ciemnej energii itp.

Aby przyspieszyć badanie ponad 26 000 galaktyk, Stephen A. Shectmanzaprojektował instrument zdolny do jednoczesnego pomiaru 112 galaktyk. W metalowej płycie wywiercono otwory odpowiadające pozycjom galaktyk na niebie. Kable światłowodowe przenosiły światło z każdej galaktyki do oddzielnego kanału na spektrografie przy 2,5-metrowym teleskopie du Pont wCarnegie Observatories na Cerro Las Campanas w Chile.

Aby uzyskać maksymalną wydajność, wyspecjalizowana technika znana jako Drift-Scan Photometryzostał użyty, w którym teleskop był skierowany na początek pola pomiarowego, a następnie wyłączono napęd automatyczny. Teleskop stał nieruchomo, gdy niebo przepływało obok. Komputery odczytują informacje zCCD Detectorw tym samym tempie co obrót Ziemi, tworząc jeden długi, ciągły obraz na stałej szerokości geograficznej niebieskiej. Wykonanie fotometrii zajęło łącznie 450 godzin.

Istnieją różne formy szumu, a ich modelowanie matematyczne różni się w zależności od jego właściwości. Różne procesy fizyczne powodują ewolucję widma mocy wszechświata na dużą skalę. Początkowe widmo mocy nadane w wyniku fluktuacji kwantowych następuje po ujemnej trzeciej potęgi częstotliwości, która jest formąPink Noise Spectrum w trzech wymiarach.

Metryka

W kosmologii najpierw trzeba mieć definicję przestrzeni. Metryka to wyrażenie matematyczne opisujące punkty w przestrzeni. Obserwacja nieba odbywa się w geometrii sferycznej; dlatego należy zastosować sferyczny układ współrzędnych. Odległość między dwoma blisko położonymi punktami jest określona wzorem -

$$ds^2 = dr^2 + r^2\theta ^2 + r^2 sin^2\theta d\phi^2$$

Poniższy rysunek przedstawia geometrię w trójwymiarowej nierozszerzającej się przestrzeni euklidesowej.

Ta geometria nadal znajduje się w trójwymiarowej nierozszerzającej się przestrzeni euklidesowej. Stąd siatka odniesienia definiująca samą ramę będzie się rozszerzać. Poniższy obraz przedstawia zwiększoną metrykę.

Współczynnik skali jest wprowadzany do równania nierozszerzającej się przestrzeni, zwanego „współczynnikiem skali”, który obejmuje rozszerzanie się wszechświata względem czasu.

$$ds^2 = a^2(t)\left [ dr^2 + r^2\theta^2 + r^2 sin^2\theta d\phi^2 \right ]$$

gdzie a(t) to współczynnik skali, czasami zapisywany jako R(t). Natomiast,a(t) > 1 oznacza powiększenie metryki, podczas gdy a(t) < 1 oznacza kurczenie się metryki i a(t) = 1oznacza stałą metrykę. Zgodnie z konwencjąa(t₀) = 1.

Ruchomy układ współrzędnych

W Comoving Coordinate System, skala pomiarowa rozszerza się wraz z ramą (rozszerzający się wszechświat).

Tutaj $\left [ dr^2 + r^2\theta^2 + r^2 sin^2\theta d\phi^2 \right ]$ jest odległością Comoving, a $ds^2$ to odległość właściwa.

Właściwa odległość będzie odpowiadać rzeczywistej odległości zmierzonej od odległej galaktyki od Ziemi w momencie obserwacji, czyli chwilowej odległości obiektów.

Dzieje się tak, ponieważ odległość pokonana przez foton, gdy dotrze do obserwatora z odległego źródła, będzie taka sama, jak ta otrzymana w $t=t_0$ obserwatora, co oznaczałoby, że chwilowa obserwowana odległość będzie właściwą odległością i można przewidzieć przyszłe odległości wykorzystując współczynnik szybkości i początkową zmierzoną długość jako odniesienie.

Pojęcie Comoving i właściwej odległości jest ważne przy pomiarze rzeczywistej wartości gęstości liczbowej galaktyk w danej objętości obserwowanej przestrzeni. Na podstawie odległości Comoving należy obliczyć gęstość w momencie ich powstania, kiedy wyemitowano obserwowany foton. Można to uzyskać po oszacowaniu tempa rozszerzania się wszechświata.

Aby oszacować tempo ekspansji, można zaobserwować zmianę odległości obserwowanej odległej galaktyki w długim okresie czasu.

Punkty do zapamiętania

• Metryka to wyrażenie matematyczne opisujące punkty w przestrzeni.

• Współczynnik skali określa, czy wszechświat kurczy się, czy rozszerza.

• W współrzędnym układzie współrzędnych skala pomiarowa rozszerza się wraz z ramką (rozszerzający się wszechświat).

• Właściwa odległość to chwilowa odległość obiektów.

• Odległość w drodze to rzeczywista odległość obiektów.

W tym rozdziale zrozumiemy szczegółowo metrykę Robertsona-Walkera.

Model zmiany współczynnika skali w czasie

Załóżmy, że foton jest emitowany z odległej galaktyki. Przestrzeń jest skierowana do przodu dla fotonów we wszystkich kierunkach. Ekspansja wszechświata odbywa się we wszystkich kierunkach. Zobaczmy, jak zmienia się współczynnik skali w czasie w kolejnych krokach.

Step 1 - W przypadku statycznego wszechświata współczynnik skali wynosi 1, tj. Wartość odległości współpoślizgowej to odległość między obiektami.

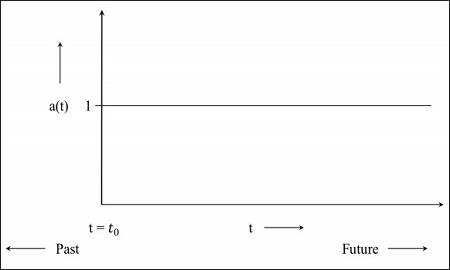
Step 2- Poniższy obraz przedstawia wykres wszechświata, który wciąż się rozszerza, ale w malejącym tempie, co oznacza, że ​​wykres rozpocznie się w przeszłości. Plikt = 0 wskazuje, że wszechświat zaczął się od tego punktu.

Step 3 - Poniższy obraz przedstawia wykres wszechświata, który rozszerza się w szybszym tempie.

Step 4 - Poniższy obraz przedstawia wykres wszechświata, który zaczyna się kurczyć od teraz.

Jeśli wartość współczynnika skali stanie się 0 podczas kurczenia się wszechświata oznacza to odległość między obiektami 0, czyli właściwa odległość staje się 0. Odległość zbliżająca się, która jest odległością między obiektami w obecnym wszechświecie, jest wielkością stałą. W przyszłości, gdy współczynnik skali stanie się0, wszystko będzie bliżej. Model zależy od składnika wszechświata.

Metryka dla płaskiego (euklidesowego: nie ma parametru dla krzywizny) rozszerzającego się wszechświata jest podana jako -

$$ds^2 = a^2(t)\left ( dr^2+r^2d\theta^2+r^2sin^2\theta d\varphi^2 \right )$$

Dla czasoprzestrzeni element liniowy, który otrzymaliśmy w powyższym równaniu, jest modyfikowany jako -

$$ds^2 = c^2dt^2 - \left \{ a^2(t) \left ( dr^2 + r^2d\theta ^2 + r^2sin^2\theta d\varphi^2 \right ) \right \}$$

W przypadku czasoprzestrzeni czas, w którym foton jest emitowany i kiedy jest wykrywany, jest inny. Właściwa odległość to chwilowa odległość do obiektów, która może się zmieniać w czasie w wyniku rozszerzania się wszechświata. Jest to odległość, jaką foton pokonał z różnych obiektów, aby się do nas dostać. Jest to związane z odległością towarzyszącą jako -

$$d_p = a(t) \times d_c$$

gdzie $d_p$ to właściwa odległość i $d_c$ to odległość zbliżająca się, która jest stała.

Odległość zmierzona do obiektów w obecnym wszechświecie jest traktowana jako odległość do współrzędnych, co oznacza, że ​​odległość między nimi jest stała i pozostaje niezmieniona przez ekspansję. W przeszłości współczynnik skali był mniejszy niż 1, co wskazuje, że właściwa odległość była mniejsza.

Możemy zmierzyć przesunięcie ku czerwieni galaktyki. Stąd odpowiednia odległość$d_p$ koresponduje z $c \times t(z)$, gdzie $t(z)$to czas obserwacji w kierunku przesunięcia ku czerwieni, a c to prędkość światła w próżni. Okres ważności jest funkcją przesunięcia ku czerwieni(z).

W oparciu o powyższe pojęcie przeanalizujmy, jak kosmologiczne przesunięcie ku czerwieni jest interpretowane w tym scenariuszu $d_p = a(t) \times d_c$.

Załóżmy, że galaktyka emituje foton (związany z ziemią), G. The $t_{em}$ odpowiada czasowi wyemitowania fotonu; $a(t_{em})$był współczynnikiem skali w momencie wyemitowania fotonu. W momencie wykrycia fotonu cały wszechświat się rozszerzył, tj. Foton jest przesunięty ku czerwieni w momencie wykrycia. Plik$t_{obs}$ odpowiada czasowi wykrycia fotonu i odpowiadającemu współczynnikowi skali $a(t_{obs})$.

Czynnik, dzięki któremu wszechświat się rozrósł, jest określony przez:

$$\frac{a(t_{obs})}{a(t_{em})}$$

Czynnikiem, o który rozszerzyła się długość fali, jest -

$$\frac{\lambda_{obs}}{\lambda_{em}}$$

która jest równa czynnikowi, dzięki któremu wszechświat urósł. Symbole mają swoje zwykłe znaczenie. W związku z tym,

$$\frac{a(t_{obs})}{a(t_{em})} = \frac{\lambda_{obs}}{\lambda_{em}}$$

Znamy to przesunięcie ku czerwieni (z) jest -

$$z=\frac{\lambda_{obs} - \lambda_{em}}{\lambda_{em}} = \frac{\lambda_{obs}}{\lambda_{em}} - 1$$

$$1 + z = \frac{a(t_{obs})}{a(t_{em})}$$

Bieżąca wartość współczynnika skali wynosi zatem 1 $a(t_{obs}) = 1$ i oznaczający współczynnik skali, kiedy foton był emitowany w przeszłości przez $a(t)$.

W związku z tym,

$$1 + z = \frac{1}{a(t)}$$

Interpretacja przesunięcia ku czerwieni w kosmologii

Aby to zrozumieć, weźmy następujący przykład: Jeśli $z = 2$ następnie $a(t) = 1/3$.

Oznacza to, że wszechświat rozszerzył się trzykrotnie, odkąd światło opuściło ten obiekt. Długość fali odbieranego promieniowania zwiększyła się trzykrotnie, ponieważ przestrzeń powiększyła się o ten sam współczynnik podczas jego przejścia od emitującego obiektu. Należy zauważyć, że przy tak dużych wartościachz, przesunięcie ku czerwieni jest głównie kosmologicznym przesunięciem ku czerwieni i nie jest poprawną miarą rzeczywistej prędkości recesji obiektu względem nas.

Dla kosmicznego mikrofalowego tła (CMB), z = 1089, co oznacza, że ​​obecny wszechświat rozszerzył się o współczynnik ∼1090. Metryka płaskiego, euklidesowego, rozszerzającego się wszechświata jest podawana jako -

$$ds^2 = a^2(t)(dr^2 + r^2d\theta^2 + r^2sin^2\theta d\varphi^2)$$

Chcemy zapisać metrykę w dowolnej krzywizny.

Robertson and Walker udowodniono dla dowolnego wszechświata krzywizny (który jest jednorodny i izotropowy), metryka jest podawana jako -

$$ds^2 = a^2(t) \left [ \frac{dr^2}{1-kr^2} + r^2d\theta^2 + r^2sin^2\theta d\varphi^2 \right ]$$

Jest to ogólnie znane jako Robertson–Walker Metrici jest prawdziwe dla każdej topologii przestrzeni. Zwróć uwagę na dodatkowy czynnik w$dr^2$. Tutaj jest stałą krzywizny.

Geometria Wszechświata

Geometria Wszechświata jest wyjaśniona za pomocą następujących krzywizn, które obejmują:

• Dodatnia krzywizna
• Ujemna krzywizna
• Zero krzywizny

Rozumiemy szczegółowo każdy z nich.

Dodatnia krzywizna

Jeśli płaszczyzna styczna narysowana w dowolnym punkcie na powierzchni krzywizny nie przecina się w żadnym punkcie na powierzchni, nazywa się to powierzchnią z dodatnią krzywizną, czyli powierzchnia pozostaje w tym punkcie po jednej stronie płaszczyzny stycznej. Powierzchnia kuli ma dodatnią krzywiznę.

Ujemna krzywizna

Jeśli płaszczyzna styczna narysowana w punkcie na powierzchni krzywizny przecina się w dowolnym miejscu na powierzchni, nazywa się to powierzchnią o ujemnej krzywizny, tj. Powierzchnia zakrzywia się od płaszczyzny stycznej w dwóch różnych kierunkach. Powierzchnia w kształcie siodła ma ujemną krzywiznę.

Rozważmy teraz powierzchnię kuli. Jeśli trójkąt jest zbudowany na powierzchni kuli przez połączenie trzech punktów geodezyjnych (łuk wielkich okręgów), to suma kątów wewnętrznych trójkąta sferycznego jest większa niż 180 ^o , czyli -

$$\alpha + \beta + \gamma > \pi$$

Takie przestrzenie nazywane są przestrzeniami zakrzywionymi dodatnio. Ponadto krzywizna jest jednorodna i izotropowa. Ogólnie kąt w wierzchołkach trójkąta sferycznego jest zgodny z zależnością -

$$\alpha + \beta +\gamma = \pi + A/R^2$$

gdzie A jest obszarem trójkąta i Rjest promieniem kuli. Poniższy obraz przedstawia pozytywnie zakrzywioną przestrzeń.

Aby uzyskać dodatnią krzywiznę, równoległe linie powinny się spotkać. Rozważmy powierzchnię ziemi, która jest przestrzenią o pozytywnym zakrzywieniu. Weź dwa punkty początkowe na równiku. Linie, które przecinają równik pod kątem prostym, nazywane są liniami długości geograficznej. Ponieważ te linie przecinają równik pod kątem prostym, można je nazwać liniami równoległymi. Zaczynając od równika, ostatecznie przecinają się na biegunach. Ta metoda była używana przezCarl Gauss i inni, aby zrozumieć topologię Ziemi.

Rozważ negatywnie - zakrzywioną przestrzeń (siodło pokazane na poniższym obrazku), suma kątów wewnętrznych trójkąta jest mniejsza niż 180 ^o , czyli -

$$\alpha + \beta + \gamma < \pi$$

Kąt na wierzchołkach jest zgodny z relacją -

$$\alpha + \beta + \gamma = \pi - A/R^2$$

Zero krzywizny

Płaska powierzchnia ma zerową krzywiznę. Teraz dla płaskiej przestrzeni, jeśli weźmie się płaszczyznę i skonstruuje się trójkąt przez połączenie trzech punktów geodezyjnymi (liniami prostymi), wewnętrzna suma kątów wyniesie

$$\alpha + \beta + \gamma = \pi$$

Poniższy obraz przedstawia płaską, dwuwymiarową przestrzeń.

Jeśli chce się, aby przestrzeń była jednorodna i izotropowa, pozostają tylko trzy możliwości: przestrzeń może być jednolicie płaska, może mieć jednolitą krzywiznę dodatnią lub jednolitą krzywiznę ujemną.

Stała krzywizny może przyjmować dowolną z następujących trzech wartości.

$$k = \begin{cases}+1, & for \: a\: positively \: curved\: space;\\\quad 0, & for\: a \: flat \: space;\\-1, & for\: a \: negatively \: curved \: space;\end{cases}$$

Globalna topologia Wszechświata

Wszechświat ma określoną topologię, ale lokalnie może mieć zmarszczki. W zależności od tego, jak materia jest rozłożona w przestrzeni, występują mniejsze różnice w krzywizny. Załóżmy, że istnieje klasa obiektów, które mają ten sam rzeczywisty rozmiar niezależnie od tego, gdzie się znajdują we Wszechświecie, co oznacza, że ​​są jak standardowe świece. Nie mają tej samej jasności, ale mają ten sam rozmiar.

Jeśli obiekt znajduje się w dodatnio zakrzywionej przestrzeni, a fotony pochodzą z punktu A (jeden koniec obiektu) i B (drugi koniec obiektu), fotony będą propagować równolegle w dodatnio zakrzywionej przestrzeni przez ścieżkę geodezyjną i ostatecznie spotkają się . Dla obserwatora w C wydaje się, że pochodzi z dwóch różnych punktów w różnych kierunkach.

Jeśli obiekt znajduje się we wszechświecie lokalnym i mierzymy rozmiar kątowy, krzywizna nie ma na niego wpływu. Jeśli ta sama klasa obiektów jest widoczna z większym przesunięciem ku czerwieni, rozmiar kątowy nie jest skorelowany z.

$$\theta = \frac{d}{r}$$

Gdzie d jest rozmiarem obiektu i rjest odległością od obiektu, tj. jeśli rozmiar jest większy niż rozmiar lokalny, oznacza to, że krzywizna jest dodatnia. Poniższy obraz przedstawia foton wykryty w dodatnio zakrzywionej przestrzeni.

Należy zauważyć, że nie ma prawdziwego obiektu astrofizycznego, który miałby standardowe rozmiary i morfologię. Chociaż uważano, że masywne eliptyczne galaktyki cD - pasują do standardowych świec, okazało się jednak, że ewoluują one z czasem.

Znajdowanie odległości do galaktyk

W tej sekcji omówimy, jak znaleźć odległość do galaktyki, biorąc pod uwagę poniższy obraz.

Rozważ Drogę Mleczną w (r, θ,) w kosmologicznej ramie spoczynku. Można przyjąć = 0; (0, θ, ϕ), czyli centrum wszechświata przez przywołanie założenia jednorodności.

Rozważmy galaktykę „G” w (r1, θ,). Odległość (właściwa) to najkrótsza promieniowa odległość przebyta przez foton. Z symetrii czasoprzestrzeni zerowa geodezyjna od r = 0 do r = r1 ma stały kierunek w przestrzeni. Współrzędne kątowe podczas propagacji radialnej nie zmieniają się. Jeśli zmieniają się współrzędne kątowe, nie jest to najkrótsza droga. To jest powód, dla którego pojęcie krzywizny występuje w dr ² .

Punkty do zapamiętania

• Ekspansja wszechświata odbywa się we wszystkich kierunkach.

• Wszechświat może być statyczny, rozszerzać się lub kurczyć w zależności od ewolucji współczynnika skali.

• Galaktyki cD ewoluują z upływem czasu i dlatego nie mogą być używane jako standardowe świece.

• Wszechświat ma pewną topologię, ale lokalnie może mieć zmarszczki.

W tym rozdziale omówimy parametry Hubble'a oraz współczynnik skali.

• Prerequisite - Kosmologiczne przesunięcie ku czerwieni, zasady kosmologiczne.

• Assumption - Wszechświat jest jednorodny i izotropowy.

Stała Hubble'a z ułamkową szybkością zmiany współczynnika skali

W tej sekcji odniesiemy Stałą Hubble'a do ułamkowej szybkości Zmiany Współczynnika Skali.

Prędkość możemy zapisać w następujący sposób i uprościć.

$$v = \frac{\mathrm{d} r_p}{\mathrm{d} t}$$

$$= \frac{d[a(t)r_c}{dt}$$

$$v = \frac{\mathrm{d} a}{\mathrm{d} t} \ast \frac{1}{a} \ast (ar_c)$$

$$v = \frac{\mathrm{d} a}{\mathrm{d} t} \ast \frac{1}{a} \ast r_p$$

Tutaj, v to prędkość recesji, a jest współczynnikiem skali i r_p to właściwa odległość między galaktykami.

Hubble’s Empirical Formula miał charakter -

$$v = H \ast r_p$$

Zatem porównując powyższe dwa równania otrzymujemy -

Hubble’s Parameter = Fractional rate of change of the scale factor

$$H = da/dt \ast 1/a$$

Note- To nie jest stała, ponieważ współczynnik skali jest funkcją czasu. Dlatego nazywa się to parametrem Hubble'a, a nie stałą Hubble'a.

Empirycznie piszemy -

$$H = V/D$$

Zatem z tego równania możemy wywnioskować, że od tego czasu D rośnie i V jest więc stałą H zmniejsza się wraz z upływem czasu i rozszerzaniem się wszechświata.

Równanie Friedmanna w połączeniu z modelem Robertsona-Walkera

W tej sekcji zrozumiemy, w jaki sposób równanie Friedmanna jest używane w połączeniu z modelem Robertsona-Walkera. Aby to zrozumieć, weźmy następujący obraz, który przedstawia masę testową w oddalir_p z masy ciała M jako przykład.

Biorąc pod uwagę powyższy obraz, możemy wyrazić siłę jako -

$$F = G \ast M \ast \frac{m}{r^2_p}$$

Tutaj, G jest uniwersalną stałą grawitacyjną, a ρ jest gęstością materii wewnątrz obserwowalnego wszechświata.

Teraz zakładając jednakową gęstość masy w kuli, możemy napisać -

$$M = \frac{4}{3} \ast \pi \ast r_p^3 \ast \rho$$

Używając ich z powrotem w naszym równaniu siły, otrzymujemy -

$$F = \frac{4}{3} \ast \pi \ast G \ast r_p \ast \rho \ast m$$

W ten sposób możemy zapisać energię potencjalną i energię kinetyczną masy m jako -

$$V = -\frac{4}{3} \ast \pi \ast G \ast r^2_p \ast m \ast \rho$$

$$K.E = \frac{1}{2} \ast m \ast \frac{\mathrm{d} r_p^2}{\mathrm{d} t}$$

Używając Virial Theorem -

$$U = K.E + V$$

$$U = \frac{1}{2} \ast m \ast \left ( \frac{\mathrm{d} r_p}{\mathrm{d} t} \right )^2 - \frac{4}{3} \ast \pi \ast G \ast r_p^2 \ast m \ast \rho$$

Ale tu, $r_p = ar_c$. Więc otrzymujemy -

$$U = \frac{1}{2} \ast m \ast \left ( \frac{\mathrm{d} a}{\mathrm{d} t} \right )^2 r_c^2 - \frac{4}{3} \ast \pi \ast G \ast r_p^2 \ast m \ast \rho$$

Przy dalszym uproszczeniu otrzymujemy równanie Friedmanna,

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi}{3} \ast G \ast \rho + \frac{2U}{m} \ast r_c^2 \ast a^2$$

Tutaj Ujest stała. Zauważamy również, że wszechświat, w którym obecnie żyjemy, jest zdominowany przez materię, podczas gdy gęstość energii promieniowania jest bardzo niska.

Punkty do zapamiętania

• Parametr Hubble'a zmniejsza się wraz z upływem czasu i rozszerzaniem się wszechświata.

• Wszechświat, w którym obecnie żyjemy, jest zdominowany przez materię, a gęstość energii promieniowania jest bardzo niska.

W tym rozdziale zrozumiemy, czym jest równanie Friedmanna i przestudiujemy szczegółowo modele świata dla różnych stałych krzywizny.

Równanie Friedmanna

To równanie mówi nam o rozszerzaniu się przestrzeni w jednorodnych i izotropowych modelach wszechświata.

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho + \frac{2U}{mr_c^2a^2}$$

Zostało to zmodyfikowane w kontekście General Relativity (GR) i Robertson-Walker Metric w następujący sposób.

Korzystanie z równań GR -

$$\frac{2U}{mr_c^2} = -kc^2$$

Gdzie kjest stałą krzywizny. W związku z tym,

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8 \pi G}{3}\rho - \frac{kc^2}{a^2}$$

Również, $\rho$zastępuje się gęstością energii, która obejmuje materię, promieniowanie i wszelkie inne formy energii. Ale dla celów reprezentacyjnych jest napisane jako$\rho$.

Modele światowe dla różnych stałych krzywizny

Przyjrzyjmy się teraz różnym możliwościom w zależności od wartości stałych krzywizny.

Przypadek 1: k = 1 lub Wszechświat zamknięty

Dla rozszerzającego się wszechświata, $da/dt > 0$. W miarę kontynuowania ekspansji pierwszy człon na RHS powyższego równania ma postać$a^{-3}$, podczas gdy druga kadencja idzie jak $a^{-2}$. Kiedy te dwa składniki stają się równe, wszechświat zatrzymuje ekspansję. Następnie -

$$\frac{8 \pi G}{3}\rho = \frac{kc^2}{a^2}$$

Tutaj k = 1, dlatego

$$a = \left [ \frac{3c^2}{8 \pi G\rho} \right ]^{\frac{1}{2}}$$

Taki wszechświat jest skończony i ma skończoną objętość. Nazywa się to Wszechświatem Zamkniętym.

Przypadek 2: k = -1 lub Open Universe

Gdyby k < 0ekspansja nigdy by się nie zatrzymała. Po pewnym czasie pierwszy termin na RHS można pominąć w porównaniu z drugim terminem.

Tutaj k = -1. W związku z tym,$da/dt ∼ c$.

W tym przypadku wszechświat płynie. Taki wszechświat ma nieskończoną przestrzeń i czas. Nazywa się to otwartym wszechświatem.

Przypadek 3: k = 0 lub Flat Universe

W tym przypadku wszechświat rozszerza się w malejącym tempie. Tutaj k = 0. Dlatego

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho$$

Taki wszechświat ma nieskończoną przestrzeń i czas. Nazywa się to płaskim wszechświatem.

Punkty do zapamiętania

• Równanie Friedmanna mówi nam o rozszerzaniu się przestrzeni w jednorodnych i izotropowych modelach wszechświata.

• W zależności od różnych wartości stałych krzywizny, możemy mieć Wszechświat Zamknięty, Otwarty lub Płaski.

W tym rozdziale omówimy równanie płynów i to, jak mówi nam o gęstości wszechświata, która zmienia się w czasie.

Szacowanie ρ _c i ρ we współczesnym wszechświecie

Dla obecnego wszechświata -

$$\rho_c \simeq 10^{11}M_\odot M_{pc}^{-3} \simeq 10\: hydrogen \: atoms \: m^{-3}$$

W naszej przestrzeni kosmicznej istnieje cały szereg krytycznych gęstości. Na przykład dla ośrodka międzygalaktycznego$\rho_c$ oznacza 1 atom wodoru $m^{-3}$podczas gdy w przypadku chmur molekularnych tak jest $10^6$ atomy wodoru $m^{−3}$.

Musimy mierzyć $\rho_c$biorąc pod uwagę odpowiednie próbki przestrzeni. W naszej galaktyce wartość$\rho_c$jest bardzo wysoka, ale nasza galaktyka nie jest reprezentantem całego wszechświata. Powinniśmy więc wyruszyć w kosmos, w którym obowiązuje zasada kosmologiczna, tj. Odległości ≈ 300 Mpc. Spojrzenie na 300 Mpc oznacza spojrzenie 1 miliard lat wstecz, ale to wciąż obecny wszechświat.

Badania, takie jak SDSS, są przeprowadzane w celu określenia rzeczywistej gęstości materii. Pobierają objętość 5 × 500 × 5 Mpc ³ , liczą galaktyki i dodają całe światło pochodzące z tych galaktyk. Przy założeniu, że 1 L ≡ 1 M, czyli 1 słoneczna Jasność ≡ 1 masa słoneczna.

Wykonujemy konwersję światła na masę, a następnie próbujemy oszacować liczbę barionów na podstawie widzialnych cząstek materii obecnych w tej objętości.

Na przykład,

$$1000L_\odot ≡ 1000M_\odot / m_p$$

Gdzie m _p = masa protonu.

Następnie otrzymujemy z grubsza gęstość liczb barionowych $\Omega b ∼= 0.025$. To sugeruje$\rho b = 0.25%$ z $\rho_c$. Różne ankiety dały nieco inną wartość. Zatem we wszechświecie lokalnym gęstość liczbowa widzialnej materii jest znacznie mniejsza niż gęstość krytyczna, co oznacza, że ​​żyjemy w otwartym wszechświecie.

W badaniach nie uwzględniono masy o współczynniku 10, ponieważ badania te uwzględniają promieniowanie elektromagnetyczne, ale nie ciemną materię. Dający,$\Omega_m = 0.3 − 0.4$. Wciąż dochodzi do wniosku, że żyjemy w otwartym wszechświecie.

Ciemna materia oddziałuje z grawitacją. Duża ilość ciemnej materii może powstrzymać ekspansję. Nie ustaliliśmy jeszcze, jak to zrobić$\rho$ zmienia się w czasie, do czego potrzebny jest kolejny zestaw równań.

Termodynamika stwierdza, że ​​-

$$dQ = dU + dW$$

W przypadku systemu rosnącego pod względem rozmiaru $dW = P dV$. Rozszerzanie się wszechświata jest modelowane jako adiabatyczne tj$dQ = 0$. Zatem zmiana objętości powinna nastąpić od zmiany energii wewnętrznej dU.

Weźmy określoną objętość wszechświata o jednostkowym promieniu, tj $r_c = 1$. Gdyby$\rho$ jest gęstością materiału w tej objętości przestrzeni,

$$M = \frac{4}{3} \pi a^3r_c^3 \rho$$

$$U = \frac{4}{3}\pi a^3\rho c^2$$

Gdzie, Uto gęstość energii. Sprawdźmy, jak zmienia się energia wewnętrzna w czasie, gdy wszechświat się rozszerza.

$$\frac{\mathrm{d} U}{\mathrm{d} t} = 4 \pi a^2 \rho c^2 \frac{\mathrm{d} a}{\mathrm{d} t} + \frac{4}{3}\pi a^3 c^2\frac{\mathrm{d} \rho}{\mathrm{d} t}$$

Podobnie, zmiana objętości w czasie jest określona wzorem:

$$\frac{\mathrm{d} V}{\mathrm{d} t} = 4\pi a^2 \frac{\mathrm{d} a}{\mathrm{d} t}$$

Zastępowanie $dU = −P dV$. Otrzymujemy,

$$4\pi a^2(c^2 \rho +P)\dot{a}+\frac{4}{3}\pi a^3c^2\dot{\rho} = 0$$

$$\dot{\rho}+3\frac{\dot{a}}{a}\left ( \rho + \frac{P}{c^2} \right ) = 0$$

Nazywa się to Fluid Equation. Mówi nam, jak gęstość wszechświata zmienia się w czasie.

Ciśnienie spada wraz z rozszerzaniem się wszechświata. W każdej chwili ciśnienie się zmienia, ale nie ma różnicy ciśnień między dwoma punktami rozważanej objętości, więc gradient ciśnienia wynosi zero. Tylko relatywistyczne materiały wywierają nacisk, materia jest bezciśnieniowa.

Równanie Friedmanna wraz z równaniem płynów modeluje wszechświat.

Punkty do zapamiętania

• Ciemna materia oddziałuje z grawitacją. Duża ilość ciemnej materii może powstrzymać ekspansję.

• Fluid Equation mówi nam, jak gęstość wszechświata zmienia się w czasie.

• Równanie Friedmanna wraz z równaniem płynów modeluje wszechświat.

• Tylko relatywistyczne materiały wywierają nacisk, materia jest bezciśnieniowa.

W tym rozdziale omówimy rozwiązania równań Friedmanna związane ze wszechświatem zdominowanym przez materię. W kosmologii, ponieważ widzimy wszystko w dużej skali, układy słoneczne, galaktyki, wszystko jest jak cząsteczki pyłu (tak to widzimy na własne oczy), możemy to nazwać wszechświatem pyłowym lub tylko wszechświatem materii.

w Fluid Equation,

$$\dot{\rho} = -3\left ( \frac{\dot{a}}{a} \right )\rho -3\left ( \frac{\dot{a}}{a} \right )\left ( \frac{P}{c^2} \right )$$

Widzimy, że istnieje presja. Dla zakurzonego wszechświataP = 0, ponieważ gęstość energii materii będzie większa niż ciśnienie promieniowania, a materia nie porusza się z relatywistyczną prędkością.

Więc równanie płynów stanie się,

$$\dot{\rho} = -3\left ( \frac{\dot{a}}{a} \right )\rho$$

$$\Rightarrow \dot{\rho}a + 3\dot{a}\rho = 0$$

$$\Rightarrow \frac{1}{a^3}\frac{\mathrm{d}}{\mathrm{d} t}(a^3 \rho) = 0$$

$$\Rightarrow \rho a^3 =\: constant$$

$$\Rightarrow \rho \propto \frac{1}{a^3}$$

W tym równaniu nie ma sprzecznych intuicji, ponieważ gęstość powinna skalować się jako $a^{-3}$ ponieważ głośność rośnie jako $a^3$.

Z ostatniej relacji możemy powiedzieć, że

$$\frac{\rho (t)}{\rho_0} = \left [ \frac{a_0}{a(t)} \right ]^3$$

Dla obecnego wszechświata a, co jest równe a₀ powinno być 1. Więc

$$\rho(t) = \frac{\rho_0}{a^3}$$

W płaskim wszechświecie zdominowanym przez materię, k = 0. Zatem równanie Friedmanna stanie się:

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8 \pi G\rho}{3}$$

$$\dot{a}^2 = \frac{8\pi G \rho a^2}{3}$$

Rozwiązując to równanie, otrzymamy:

$$a \propto t^{2/3}$$

$$\frac{a(t)}{a_0} = \left ( \frac{t}{t_0} \right )^{2/3}$$

$$a(t) = \left( \frac{t}{t_0} \right )^{2/3}$$

Oznacza to, że wszechświat będzie wzrastał w malejącym tempie. Poniższy obraz przedstawia ekspansję Zakurzonego Wszechświata.

Jak ρ zmienia się z czasem?

Spójrz na następujące równanie -

$$\frac{\rho(t)}{\rho_0} = \left ( \frac{t_0}{t} \right )^2$$

Wiemy, że współczynnik skali zmienia się z czasem jako $t^{2/3}$. Więc,

$$a(t) = \left ( \frac{t}{t_0} \right )^{2/3}$$

Różnicując to, otrzymamy,

$$\frac{(da)}{dt} = \dot{a} = \frac{2}{3} \left ( \frac{t^{-1/3}}{t_0} \right )$$

Wiemy, że Hubble Constant jest,

$$H(t) = \frac{\dot{a}}{a} = \frac{2}{3t}$$

To jest równanie Einstein-de sitter Universe. Jeśli chcemy obliczyć obecny wiek wszechświata,

$$t_0 = t_{age} = \frac{2}{3H_0}$$

Po wpisaniu wartości $H_0$ dla obecnego wszechświata otrzymamy wartość wieku wszechświata jako 9 Gyrs. Jest wieleGlobular Cluster w naszej własnej galaktyce Drogi Mlecznej, która ma więcej lat.

Chodziło o zakurzony wszechświat. Jeśli przyjmiemy, że wszechświat jest zdominowany przez promieniowanie, a nie materię, to gęstość energii promieniowania będzie taka sama$a^{-4}$ zamiast $a^{-3}$. Więcej tego dowiemy się w następnym rozdziale.

Punkty do zapamiętania

• W kosmologii wszystko jest jak cząsteczki pyłu, dlatego nazywamy to wszechświatem pyłowym lub wszechświatem tylko materii.

• Jeśli przyjmiemy, że wszechświat jest zdominowany przez promieniowanie, a nie przez materię, to gęstość energii promieniowania jest taka sama $a^{-4}$ zamiast $a^{-3}$.

W tym rozdziale omówimy rozwiązania równań Friedmanna odnoszące się do wszechświata zdominowanego przez promieniowanie. Na początku porównujemy gęstość energii materii z gęstością promieniowania. To pozwoli nam zobaczyć, czy nasz wszechświat jest zdominowany przez materię, czy zdominowany przez promieniowanie.

Gęstość energii promieniowania

Promieniowanie panujące w obecnym wszechświecie można w bardzo niewielkim stopniu przypisać źródłom gwiazd, ale jest ono głównie spowodowane pozostałościami CMB (kosmiczne tło mikrofalowe).

Gęstość energii promieniowania, $\epsilon_{\gamma,0}$można wyrazić następująco:

$$\epsilon_{\gamma,0} = aT_0^4$$

Tutaj, a jest stałą promieniowania, która ma wyrażenie $(8\pi^5k_B^4)/(15h^3c^2)$ równy a = 7.5657 × 10⁻¹⁵erg\: cm⁻³ K⁻⁴. Rozważamy tutaj temperaturę T0, która odpowiada temperaturze ciała czarnego odpowiadającego CMB.

Zastępując wyniki, mamy

$$\epsilon_{\gamma,0} = aT_0^4 = 4 \times 10^{-13}erg\: cm^{-3}$$

Gęstość energii materii

W poniższych obliczeniach przyjęliśmy założenie pracy z płaskim Wszechświatem i K = 0. Rozpatrujemy gęstość energii materii jako $\epsilon = \rho c^2$. Rozważamy następujące -

$$\rho_{m,0}c^2 = 0.3\rho_{c,0}c^2 = 0.3 \times \frac{3H_0^2}{8\pi G} \times c^2$$

$$\rho_{m,0}c^2 \simeq 2 \times 10^{-8} erg \:cm^{-3}$$

$$\rho_{b,0}c^2 = 0.03\rho_{c,0}c^2 = 0.03 \times \frac{3H_0^2}{8\pi G} \times c^2$$

$$\rho_{b,0}c^2 \simeq 2 \times 10^{-9} erg\: cm^{-3}$$

Zatem z powyższego obliczenia widzimy, że żyjemy we wszechświecie zdominowanym przez materię. Potwierdza to fakt, że KMPT jest bardzo zimny. Gdy spojrzymy w przeszłość, temperatura KMPT staje się coraz wyższa i będziemy w stanie stwierdzić, że mogła istnieć epoka, w której wszechświat był zdominowany przez promieniowanie.

Zmienność gęstości i współczynnika skali

Równanie płynu pokazuje nam, że -

$$\dot{\rho} + 3\frac{\dot{a}}{a}\left ( \rho + \frac{P}{c^2} \right ) = 0$$

Jeśli weźmiemy pod uwagę zapylony wszechświat, otrzymamy P = 0. Pomijając poprzednie wyniki, uważamy, że wszechświat jest zdominowany przez promieniowanie.

$$\dot{\rho}_{rad} + 3 \frac{\dot{a}}{a}\left ( \rho_{rad} + \frac{P}{c^2} \right ) = 0$$

Wykorzystując zależność ciśnienia od $P_{rad} = \rho c^{2/3}$ mamy -

$$\dot{\rho}_{rad} + 3 \frac{\dot{a}}{a}\left ( \rho_{rad} + \frac{\rho_{rad}}{3} \right ) = 0$$

$$\dot{\rho}_{rad} + 4\frac{\dot{a}}{a}(\rho_{rad}) = 0$$

W przypadku dalszego uproszczenia mamy

$$\frac{1}{a^4}\frac{\mathrm{d}}{\mathrm{d} t}(\rho_{rad}a^4) = 0$$

$$\rho_{rad}a^4 =\: constant$$

$$\rho_{rad} \propto \frac{1}{a^4}$$

Powyższy wynik pokazuje odwrotną ^czwartą zmianę potęgi a z$\rho$.

Można to fizycznie zinterpretować jako $a^{-3}$pochodzi z wahań głośności w miarę jej wzrostu. Pozostali$a^{-1}$można traktować jako energię utraconą przez foton w wyniku ekspansji przestrzeni we wszechświecie (kosmologiczne przesunięcie ku czerwieni 1 + z = a ^-1 ).

Poniższy obraz przedstawia zmiany gęstości materii i promieniowania w czasie.

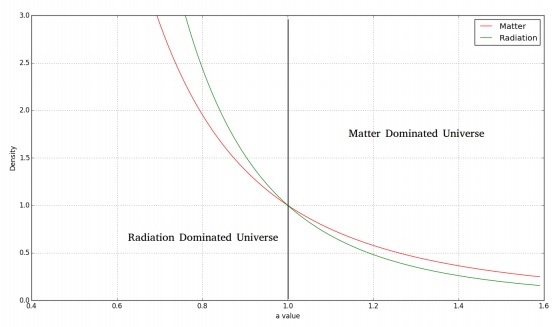
W przypadku płaskiego wszechświata zdominowanego przez promieniowanie otrzymalibyśmy następujące równanie Friedmanna -

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G\rho}{3}$$

$$\left ( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3}\frac{\rho_0}{a^4}$$

Po uproszczeniu i zastosowaniu rozwiązania do równania różniczkowego mamy -

$$(\dot{a})^2 = \frac{8\pi G\rho_0}{3a^2}$$

$$\Rightarrow a(t) \propto t^{\frac{1}{2}}$$

Tak więc mamy -

$$a(t) = a_0 \left ( \frac{t}{t_0} \right )^{\frac{1}{2}}$$

Z powyższego równania widzimy, że tempo wzrostu współczynnika skali jest mniejsze niż w zapylonym wszechświecie.

Punkty do zapamiętania

• Promieniowanie panujące w obecnym wszechświecie można w bardzo niewielkim stopniu przypisać źródłom gwiazd.

• W zakurzonym wszechświecie ciśnienie wynosi zero.

• CMB jest bardzo zimny.

Obszar ciemnej energii jest bardzo szarym obszarem w astronomii, ponieważ jest wolnym parametrem we wszystkich równaniach, ale nie ma jasnego pojęcia, co to dokładnie jest.

Zaczniemy od równań Friedmanna,

$$\left ( \frac{\dot{a}}{a} \right)^2 = \frac{8\pi G}{3}\rho - \frac{k \ast c^2}{a^2}$$

Większość podstawowych książek o kosmologii, wszystkie zaczynają się od opisu ciemnej energii z tego epizodu, że przed obserwacją Hubble'a wszechświat jest zamknięty i statyczny.

Teraz, aby wszechświat był statyczny po prawej stronie, oba wyrazy powinny być zgodne i powinny wynosić zero, ale jeśli pierwszy człon jest większy niż drugi, to wszechświat nie będzie statyczny, więc Einstein porzucił dowolny parametr ∧ do równania pola, aby uczynić wszechświat statycznym, więc argumentował, że bez względu na to, jaki składnik pierwszy jest porównywany z drugim, zawsze można uzyskać statyczny wszechświat, jeśli w równaniu jest jeszcze jeden składnik, który może skompensować dys- pasuje między tymi dwoma terminami.

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho - \frac{k \ast c^2}{a^2} + \frac{\wedge}{3}$$

$$\left ( \frac{\ddot{a}}{a} \right ) = -\frac{4 \pi G}{3}\left ( \rho + \frac{3P}{c^2} \right ) + \frac{\wedge}{3}$$

Gdzie $P = \rho \ast c^2/3$ i $\wedge = \rho \ast c^2$jest parametrem kosmologicznym. (Znak minus jest tylko z powodu przyciągania)

W powyższym równaniu (równanie przyspieszenia) -

• $3P/c^2$ jest podciśnieniem spowodowanym promieniowaniem,

• $-4\pi G/3$ jest przyciąganiem spowodowanym grawitacją i

• $\wedge/3$ wnosi pozytywny wkład.

Trzeci człon działa jako siła odpychająca, ponieważ inna część równania jest atrakcyjna.

Fizyczne znaczenie tego równania jest takie ˙a = 0ponieważ nie było żadnych dowodów wskazujących, że wszechświat się rozszerza. A co jeśli te dwa terminy nie pasują do siebie, więc lepiej jest dodać komponent iw zależności od offsetu zawsze możemy zmienić wartość parametru free.

W tamtym czasie nie było fizycznego wyjaśnienia tych parametrów kosmologicznych, dlatego też, gdy wyjaśnienie rozszerzającego się wszechświata zostało odkryte w latach dwudziestych XX wieku, Einstein natychmiast musiałem wyrzucić tę stałą.

Wyjaśnienie tego cosmological constant jest nadal w użyciu, ponieważ wyjaśnia inną wersję wszechświata, ale definicja tej stałej kosmologicznej, sposób interpretacji zmieniał się w czasie.

Teraz koncepcja tej stałej kosmologicznej została przywrócona do kosmologii z wielu powodów. Jednym z powodów jest to, że mamy obserwacje gęstości energii różnych składników Wszechświata (barionowej, ciemnej materii, promieniowania), więc wiemy, czym jest ten parametr. Niezależne obserwacje przy użyciucosmic microwave background pokazuje, że k = 0.

$$CMB, k=0\: \rho = \rho_c = \frac{3H_0^2}{8\pi G} \approx 10 \: Hydrogen \: atoms.m^{-3}$$

Aby k było równe 0, $\rho$ powinno być równe $\rho_c$, ale wszystko, co wiemy, jeśli dodamy to, co nie daje 0, co oznacza, że ​​jest jakiś inny składnik, który pokazuje, że jest znacznie mniejszy niż $\rho_c$.

$$\rho = \rho_b + \rho_{DM} + \rho_{rad} << \rho_c$$

Jeszcze jeden dowód ciemnej energii pochodzi z Type 1 Supernova Observationco ma miejsce, gdy biały karzeł nagromadzi materię i przekroczy granicę Chandrashekhar, która jest bardzo precyzyjną granicą (≈ 1,4 M). Teraz za każdym razem, gdy dochodzi do wybuchu supernowej typu 1, mamy taką samą masę, co oznacza, że ​​całkowita energia wiązania układu jest taka sama, a ilość energii światła, którą widzimy, jest taka sama.

Oczywiście światło supernowej wzrasta, a następnie słabnie, ale jeśli mierzysz szczytową jasność, zawsze będzie ona taka sama, co czyni ją standardowym kandydatem. Tak więc za pomocą supernowej typu 1 wykorzystaliśmy do pomiaru kosmologicznego składnika Wszechświata, a astronomowie odkryli, że supernowa z dużym przesunięciem ku czerwieni jest o 30% - 40% słabsza niż supernowa o niskim przesunięciu ku czerwieni i można to wyjaśnić, jeśli nie ma -zero∧ semestr.

W modelach kosmologicznych DE (Dark Energy)jest traktowany jako płyn, co oznacza, że ​​możemy dla niego zapisać równanie stanu. Równanie stanu jest równaniem, które łączy zmienne, takie jak ciśnienie, gęstość, temperatura i objętość, dwóch różnych stanów materii.

Wymiarowo widzimy,

$$\frac{8 \pi G}{3}\rho = \frac{\wedge}{3}$$

$$\rho_\wedge = \frac{\wedge}{8\pi G}$$

Gęstość energii DE,

$$\epsilon_\wedge = \rho_\wedge \ast c^2 = \frac{\wedge c^2}{8 \pi G}$$

Parametr gęstości energii ciemnej,

$$\Omega_\wedge = \frac{\rho_\wedge}{\rho_c}$$

$\Omega_\wedge$ jest gęstością ciemnej energii pod względem gęstości krytycznej.

$$\rho = \rho_b + \rho_{DM} +\rho_\wedge$$

Istnieje wiele teorii na temat ciemnej energii, która odpycha wszechświat i powoduje jego rozszerzanie się. Jedna z hipotez głosi, że ta ciemna energia może być gęstością energii próżni. Załóżmy, że sama przestrzeń przetwarza pewną energię i kiedy policzysz ilość materii barionowej, ciemnej materii i promieniowania w jednostkowej objętości przestrzeni, liczysz również ilość energii związanej z przestrzenią, ale nie jest to jasne że ciemna energia jest w rzeczywistości gęstością energii próżni.

Wiemy, że związek między gęstością a współczynnikiem skali dla ciemnej materii i promieniowania to:

$$\rho_m \propto \frac{1}{a^3}$$

$$\rho_m \propto \frac{1}{a^4}$$

Mamy wykres współczynnika skali gęstości v / s. Widzimy to na tej samej działce$\rho_\wedge$ jest stałą z rozszerzaniem się wszechświata, która nie zależy od współczynnika skali.

Poniższy obraz przedstawia zależność między gęstością a współczynnikiem skali.

‘ρ’ v/s ‘a’(współczynnik skali, który jest powiązany z czasem) na tym samym wykresie ciemna energia jest modelowana jako stała. Zatem każda ciemna energia, którą mierzymy w obecnym wszechświecie, jest stałą.

Punkty do zapamiętania

• Niezależne obserwacje przy użyciu kosmicznego mikrofalowego tła pokazują, że k = 0.

• $\rho_\wedge$ jest stałą z rozszerzaniem się wszechświata, która nie zależy od współczynnika skali.

• Grawitacja również zmienia się z czasem, co się nazywa modified Newtonian dynamics.

W tym rozdziale omówimy krzywe rotacji galaktyk spiralnych i dowody na istnienie ciemnej materii.

Ciemna materia i obserwacyjne fakty dotyczące ciemnej materii

• Wczesnym dowodem na istnienie ciemnej materii był plik study of the Kinematics of Spiral Galaxy.

• Słońce jest przesunięte o 30 000 lat świetlnych od centrum naszej Galaktyki. Galaktyczna prędkość centryczna wynosi 220 km / s.

• Dlaczego prędkość 220 km / s to nie 100 km / s lub 500 km / s? Co rządzi ruchem kołowym obiektu?

• Masa zamknięta w promieniu pomaga wykryć prędkość we Wszechświecie.

Rotacja Drogi Mlecznej lub Galaktyki Spiralnej - Rotacja Różnicowa

• Angular Velocity zmienia się w zależności od odległości od centrum.

• Okres orbity zależy od odległości od centrum.

• Materiał bliżej centrum Galaktyki ma krótszy okres czasu, a materiał z dala od centrum Galaktyki ma dłuższy okres.

Krzywa rotacji

• Przewidzieć zmianę prędkości za pomocą Galactic centric radius. Krzywa, która podaje prędkość zmienia się wraz z promieniem orbity.

• Kiedy widzimy, jak rzeczy się poruszają, myślimy, że to grawitacja wpływa na rotację.

• Rozkład masy zmienia się wraz z promieniem. Gęstość materii pozwoli przewidzieć krzywą rotacji. Krzywa rotacji oparta na gęstości materii, która zmienia się wraz z promieniem.

Jasność powierzchni

• Wybieramy łatkę i sprawdzamy, ile wydobywa się światło.

• Ilość światła pochodzącego z łaty nazywana jest jasnością powierzchni.

• Jego jednostką jest mag/arcsec².

• Jeśli stwierdzimy, że jasność powierzchni zmienia się wraz z promieniem, możemy stwierdzić, że świecąca materia zmienia się wraz z promieniem.

  $$\mu(r) \propto exp \left( \frac{-r}{h_R} \right )$$

  $h_R$ to długość skali. $\mu(r) = \mu_o \ast exp \left( \frac{-r}{h_R} \right )$

• $h_R$ to prawie 3 kpc dla Drogi Mlecznej.

Galaktyki spiralne

Aby astronomowie mogli zrozumieć krzywą rotacji, podzielili galaktyki na dwa składniki, którymi są:

• Disk
• Bulge

Poniższa ilustracja przedstawia centralne kuliste wybrzuszenie + okrągły krążek. Rozkład gwiazd i gazów jest inny w wybrzuszeniu i dysku.

Kinematyka galaktyk spiralnych

• Prędkość kołowa dowolnego obiektu - dla wybrzuszenia wynosi (r <Rb).

  $$V^2(r) = G \ast \frac{M(r)}{r}$$

  $$M(r) = \frac{4\pi r^3}{3} \ast \rho_b$$

• Dla dysku - (Rb <r <Rd)

  $$V^2(r) = G \ast \frac{M(r)}{r}$$

• Wybrzuszenie ma mniej więcej stałą gęstość gwiazd.

• Gęstość wewnątrz wybrzuszenia jest stała (nie zmienia się wraz z odległością wewnątrz wybrzuszenia).

• W dysku gęstość gwiazd maleje wraz z promieniem. Promień wzrasta, a następnie świecąca materia maleje.

• Hurtowo - $V(r) \propto r$

• Na dysku - $V(r) \propto 1/\sqrt{r}$

Krzywa rotacyjna galaktyk spiralnych

• Przez Spectroscopy (pobliskie galaktyki - galaktyka rozdzielona przestrzennie), tworzymy krzywą rotacji.

• Jak wspomniano powyżej, widzimy, że krzywa obrotu jest płaska w obszarach zewnętrznych, tj. Rzeczy poruszają się szybko w obszarach zewnętrznych, co generalnie nie powinno mieć takiej postaci.

• Prędkość orbitalna rośnie wraz ze wzrostem promienia obszaru wewnętrznego, ale spłaszcza się w obszarze zewnętrznym.

Ciemna materia

Mówi się, że ciemna materia jest nieświecącym składnikiem wszechświata. Rozumiemy kwestię ciemnej materii dzięki następującym wskazówkom.

• Płaskie krzywe rotacji są sprzeczne z tym, co widzimy dla rozkładu gwiazd i gazu w galaktykach spiralnych.

• Jasność powierzchni dysku spada wykładniczo wraz z promieniem, co oznacza, że ​​masa świetlistej materii, głównie gwiazd, jest skoncentrowana wokół centrum galaktyki.

• Spłaszczenie krzywej rotacji sugeruje, że całkowita masa galaktyki znajduje się w pewnym promieniu r rośnie zawsze wraz ze wzrostem r.

• Można to wyjaśnić tylko wtedy, gdy w tych galaktykach występuje duża ilość niewidocznej masy grawitacyjnej, która nie emituje promieniowania elektromagnetycznego.

• Pomiary krzywej rotacji galaktyk spiralnych to jeden z najbardziej przekonujących zestawów dowodów na istnienie ciemnej materii.

Dowody na istnienie ciemnej materii

• Missing Mass - 10 razy większa od masy świetlnej.

• Większość tej ciemnej materii musi znajdować się w halo galaktyki: duże ilości ciemnej materii w dysku mogą zakłócać długoterminową stabilność dysku wobec sił pływowych.

• Niewielki ułamek ciemnej materii w dysku może być barionowo - słabe gwiazdy (brązowe karły, czarne karły) i zwarte pozostałości gwiazd (gwiazdy neutronowe, czarne dziury). Ale taka barionowa ciemna materia nie może wyjaśnić pełnej skali brakującej masy w galaktykach.

• Profil gęstości ciemnej materii - $M(r) \propto r$ i $\rho(r) \propto r^{−2}$.

• Dane krzywej rotacji galaktyk spiralnych są zgodne z ciemną materią rozmieszczoną w ich halo.

• To ciemne halo stanowi znaczną część całkowitej masy galaktyki.

• Cała materia barionowa (gwiazdy, gromady gwiazd, ISM itp.) Jest utrzymywana razem przez grawitacyjny potencjał tego halo ciemnej materii.

Wniosek

• Ciemną materię wykryto jedynie poprzez ich oddziaływanie grawitacyjne ze zwykłą materią. Nie zaobserwowano jeszcze interakcji ze światłem (brak siły elektromagnetycznej).

• Neutrinos- Naładuj mniej, słabo oddziałuje, ale masa jest zbyt mniejsza (<0,23 eV). Cząsteczki DM powinny mieć E> 10 eV lub więcej, aby wyjaśnić powstawanie struktury.

• Źródłem ciemnej materii mogą być słabo oddziałujące masywne cząstki (WIMPS).

Punkty do zapamiętania

• Materiał bliżej centrum Galaktyki ma krótszy okres czasu.

• Wybrzuszenie ma mniej więcej stałą gęstość gwiazd.

• Jasność powierzchni dysku spada wykładniczo wraz z promieniem.

• Duże ilości ciemnej materii w dysku mogą zakłócać długoterminową stabilność dysku wobec sił pływowych.

Pojawiły się pierwsze bezpośrednie dowody na istnienie ciemnej materii Frids Ricky. Dokonał obserwacji, które po raz pierwszy ujawniły ciemną materię. Jego obserwacje dotyczyły ogólnego ruchu w gromadzie galaktyk.

Rozległe obiekty to gromady galaktyk i uważane są za struktury związane. Galaktyki te poruszają się względem centrum gromady, ale nie odlatują. Patrzymy na ogólny ruch galaktyki.

Założenie: Prędkości reprezentują potencjał bazowy

Każda galaktyka będzie miała swój własny ruch w gromadzie i Hubble Flow Component. Mniejsze galaktyki są mniejsze, większość światła pochodzi z M31 i MW, jest kilka galaktyk karłowatych. Do naszej wstępnej analizy możemy użyć tylko M31 i MW i oszacować masę dynamiczną grupy lokalnej.

Między nami a M31 istnieje względna prędkość. To jest surowe, ale to prawda. Historia zaczyna się dawno temu, gdy M31 i MW były blisko siebie, ponieważ były członkami gromady, którą oddalali się od siebie. Po pewnym czasie osiągają maksymalną separację, po czym zbliżają się do siebie.

Powiedzmy, że maksymalne oddzielenie, jakie może kiedykolwiek osiągnąć, to $r_{max}$. Teraz mają wezwaną separacjęr. PozwolićMbyć połączoną masą MW i M31. Nie wiemy, kiedy$r_{max}$ został osiągnięty.

$$\frac{GM}{r_{max}} = \:Potential \: at \:r_{max}$$

Kiedy galaktyki te zbliżały się do siebie w pewnym momencie r, wówczas energia układu będzie wynosić -

$$\frac{1}{2}\sigma^2 = \frac{GM}{r} = \frac{GM}{r_{max}}$$

σ to prędkość względna obu galaktyk. M jest tylko masą zredukowaną, ale masa próbna wynosi 1. σ jest prędkością dowolnego obiektu na odległość rod środka klastra. Uważamy, że ta klaster jest w równaniu dynamicznym, ponieważ zachodzi twierdzenie o wirusie. Tak więc galaktyki nie mogą nadejść z inną prędkością.

Ile czasu zajmie tym galaktykom osiągnięcie maksymalnej odległości?

Aby to zrozumieć, rozważmy następujące równanie.

$$\frac{1}{2}\left ( \frac{dr}{dt} \right )^2 = \frac{GM}{r} - \frac{GM}{r_{max}}$$

$$t_{max} = \int_{0}^{r_{max}} dt = \int_{0}^{r_{max}} \frac{dr}{\sqrt{2GM}}\left ( \frac{1}{r} - \frac{1}{r_{max}} \right )^2$$

$$t_{max} = \frac{\pi r_{max}^{\frac{3}{2}}}{2\sqrt{2GM}}$$

Gdzie M = dynamiczna masa grupy lokalnej. Całkowity czas od początku do końca kolizji wynosi$2t_{max}$. W związku z tym,

$$2t_{max} = t_0 + \frac{D}{\sigma}$$

I $t_0$ to obecny wiek wszechświata.

Jeśli faktycznie $t_{max} < RHS$, wtedy mamy dolną granicę czasu. $D/\sigma$to czas, kiedy znów się zderzą. Tutaj przyjęliśmy, że σ jest stałe.

$$t_{max} = \frac{t_0}{2} + \frac{D}{2\sigma}$$

$$r_{max} = t_{max} \times \sigma = 770K_{pc}$$

Tutaj σ = prędkość względna między MW a M31.

$$M_{dynamic} = 3 \times 10^{12}M_0$$

$$M_{MW}^{lum} = 3 \times 10^{10}M_0$$

$$M_{M31}^{lum} = 3 \times 10^{10}M_0$$

Ale praktycznie masa dynamiczna jest odkrywana, biorąc pod uwagę każdą galaktykę w gromadzie. Brakująca masa to ciemna materia iFrids Rickyzauważył, że galaktyki w gromadzie w śpiączce poruszają się zbyt szybko. Przewidział istnienie gwiazd neutronowych rok po odkryciu gwiazd neutronowych i użył teleskopu Palomar do znalezienia supernowej.

Punkty do zapamiętania

• Pojawiły się pierwsze bezpośrednie dowody na istnienie ciemnej materii Frids Ricky.

• Rozszerzone obiekty to gromady galaktyk i są brane pod uwagę bound structures.

• Dynamic mass jest odkrywane, biorąc pod uwagę każdą galaktykę w gromadzie.

W tym rozdziale omówimy parametry gęstości i Hubble'a.

Parametr Hubble'a

Parametr Hubble jest zdefiniowany w następujący sposób -

$$H(t) \equiv \frac{da/dt}{a}$$

który mierzy, jak szybko zmienia się współczynnik skali. Mówiąc bardziej ogólnie, ewolucja współczynnika skali jest określona przez równanie Friedmanna.

$$H^2(t) \equiv \left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho - \frac{kc^2}{a^2} + \frac{\wedge}{3}$$

gdzie, ∧ jest kosmologiczną stałą.

Dla płaskiego wszechświata k = 0, stąd równanie Friedmanna staje się -

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho + \frac{\wedge}{3}$$

W przypadku wszechświata zdominowanego przez materię gęstość zmienia się jako -

$$\frac{\rho_m}{\rho_{m,0}} = \left ( \frac{a_0}{a} \right )^3 \Rightarrow \rho_m = \rho_{m,0}a^{-3}$$

a dla wszechświata zdominowanego przez promieniowanie gęstość zmienia się jako -

$$\frac{\rho_{rad}}{\rho_{rad,0}} = \left ( \frac{a_0}{a} \right )^4 \Rightarrow \rho_{rad} = \rho_{rad,0}a^{-4}$$

Obecnie żyjemy w wszechświecie zdominowanym przez materię. Dlatego rozważam$\rho ≡ \rho_m$otrzymujemy -

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho_{m,0}a^{-3} + \frac{\wedge}{3}$$

Stała kosmologiczna i gęstość ciemnej energii są powiązane w następujący sposób -

$$\rho_\wedge = \frac{\wedge}{8 \pi G} \Rightarrow \wedge = 8\pi G\rho_\wedge$$

Z tego otrzymujemy -

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{8\pi G}{3}\rho_{m,0}a^{-3} + \frac{8 \pi G}{3} \rho_\wedge$$

Ponadto gęstość krytyczna i stała Hubble'a są powiązane w następujący sposób -

$$\rho_{c,0} = \frac{3H_0^2}{8 \pi G} \Rightarrow \frac{8\pi G}{3} = \frac{H_0^2}{\rho_{c,0}}$$

Z tego otrzymujemy -

$$\left ( \frac{\dot{a}}{a} \right )^2 = \frac{H_0^2}{\rho_{c,0}}\rho_{m,0}a^{-3} + \frac{H_0^2}{\rho_{c,0}}\rho_\wedge$$

$$\left ( \frac{\dot{a}}{a} \right )^2 = H_0^2\Omega_{m,0}a^{-3} + H_0^2\Omega_{\wedge,0}$$

$$(\dot{a})^2 = H_0^2\Omega_{m,0}a^{-1} + H_0^2\Omega_{\wedge,0}a^2$$

$$\left ( \frac{\dot{a}}{H_0} \right )^2 = \Omega_{m,0}\frac{1}{a} + \Omega_{\wedge,0}a^2$$

$$\left ( \frac{\dot{a}}{H_0} \right )^2 = \Omega_{m,0}(1+z) + \Omega_{\wedge,0}\frac{1}{(1+z)^2}$$

$$\left ( \frac{\dot{a}}{H_0} \right)^2 (1+z)^2 = \Omega_{m,0}(1+z)^3 + \Omega_{\wedge,0}$$

$$\left ( \frac{\dot{a}}{H_0} \right)^2 \frac{1}{a^2} = \Omega_{m,0}(1 + z)^3 + \Omega_{\wedge,0}$$

$$\left ( \frac{H(z)}{H_0} \right )^2 = \Omega_{m,0}(1+z)^3 + \Omega_{\wedge,0}$$

Tutaj, $H(z)$jest parametrem Hubble'a zależnym od przesunięcia ku czerwieni. Można to zmodyfikować, aby uwzględnić parametr gęstości promieniowania$\Omega_{rad}$ i parametr gęstości krzywizny $\Omega_k$. Zmodyfikowane równanie to -

$$\left ( \frac{H(z)}{H_0} \right )^2 = \Omega_{m,0}(1+z)^3 + \Omega_{rad,0}(1+z)^4+\Omega_{k,0}(1+z)^2+\Omega_{\wedge,0}$$

$$Or, \: \left ( \frac{H(z)}{H_0} \right)^2 = E(z)$$

$$Or, \: H(z) = H_0E(z)^{\frac{1}{2}}$$

gdzie,

$$E(z) \equiv \Omega_{m,0}(1 + z)^3 + \Omega_{rad,0}(1+z)^4 + \Omega_{k,0}(1+z)^2+\Omega_{\wedge,0}$$

To pokazuje, że parametr Hubble zmienia się w czasie.

Dla Einstein-de Sitter Wszechświat, $\Omega_m = 1, \Omega_\wedge = 0, k = 0$.

Wprowadzając te wartości, otrzymujemy -

$$H(z) = H_0(1+z)^{\frac{3}{2}}$$

która pokazuje ewolucję w czasie parametru Hubble'a dla wszechświata Einsteina-de Sittera.

Parametr gęstości

Parametr gęstości, $\Omega$, definiuje się jako stosunek rzeczywistej (lub obserwowanej) gęstości ρ do gęstości krytycznej $\rho_c$. Na każdą ilość$x$ odpowiedni parametr gęstości, $\Omega_x$ można wyrazić matematycznie jako -

$$\Omega_x = \frac{\rho_x}{\rho_c}$$

Dla różnych rozważanych wielkości możemy zdefiniować następujące parametry gęstości.

S.No.	Ilość	Parametr gęstości
1	Bariony	$\Omega_b = \frac{\rho_b}{\rho_c}$
2	Materia (barionowa + ciemna)	$\Omega_m = \frac{\rho_m}{\rho_c}$
3	Ciemna energia	$\Omega_\wedge = \frac{\rho_\wedge}{\rho_c}$
4	Promieniowanie	$\Omega_{rad} = \frac{\rho_{rad}}{\rho_c}$

Gdzie symbole mają swoje zwykłe znaczenie.

Punkty do zapamiętania

• Ewolucja współczynnika skali jest określana przez Friedmann Equation.

• H(z) jest parametrem Hubble'a zależnym od przesunięcia ku czerwieni.

• Plik Hubble Parameter zmienia się w czasie.

• Plik Density Parameter definiuje się jako stosunek gęstości rzeczywistej (lub obserwowanej) do gęstości krytycznej.

Jak omówiono we wcześniejszych rozdziałach, ewolucja parametru Hubble w czasie jest określona wzorem -

$$H(z) = H_0E(z)^{\frac{1}{2}}$$

Gdzie z to przesunięcie ku czerwieni i E(Z) jest -

$$E(z) \equiv \Omega_{m,0}(1+z)^3 + \Omega(1+z)^4 +\Omega_{k,0}(1+z)^2 + \Omega^{\wedge,0}$$

Jeśli ekspansja wszechświata jest stała, to prawdziwy wiek wszechświata podaje się w następujący sposób -

$$t_H = \frac{1}{H_0}$$

Jeśli jest to wszechświat zdominowany przez materię, tj. Wszechświat Einsteina Desittera, to prawdziwy wiek wszechświata jest określony przez -

$$t_H = \frac{2}{3H_0}$$

Skala i przesunięcie ku czerwieni są definiowane przez -

$$a=\frac{a_0}{1+z}$$

Wiek Wszechświata w kategoriach parametru kosmologicznego wyprowadza się w następujący sposób.

Parametr Hubble'a jest określony przez -

$$H = \frac{\frac{da}{dt}}{a}$$

Różnicując, otrzymujemy -

$$da = \frac{-dz}{(1+z)^2}$$

Gdzie a₀ = 1 (aktualna wartość współczynnika skali)

$$\frac{\mathrm{d} a}{\mathrm{d} t} = \frac{-1}{(1+z)^2}$$

$$\frac{\mathrm{d} a}{\mathrm{d} t} = \frac{\mathrm{d} a}{\mathrm{d} t}\frac{\mathrm{d} z}{\mathrm{d} t}$$

$$H = \frac{\dot{a}}{a} = \frac{\mathrm{d} a}{\mathrm{d} t}\frac{\mathrm{d} z}{\mathrm{d} t} \frac{1+z}{1}$$

$$\frac{\dot{a}}{a} = \frac{-1}{1+z}\frac{\mathrm{d} z}{\mathrm{d} t}\frac{1}{1}$$

$$H(z) = H_0E(z)^{\frac{1}{2}}$$

$$dt = \frac{-dz}{H_0E(z)^{\frac{1}{2}}(1+z)}$$

Jeśli chcemy znaleźć wiek Wszechświata przy dowolnym przesunięciu ku czerwieni ‘z’ wtedy -

$$t(z) = \frac{1}{H_0}\int_{\infty}^{z_1} \frac{-1}{E(z)^{\frac{1}{2}}(1+z)}dz$$

Gdzie k jest parametrem gęstości krzywizny, a -

$$E(z) \equiv \Omega_{m,0}(1+z)^3 + \Omega_{rad,0}(1+z)^4 + \Omega_{k,0}(1+z)^2 + \Omega_{\wedge,0}$$

Aby obliczyć obecny wiek wszechświata, weź z₁ = 0.

$$t(z=0) = t_{age} = t_0 = \frac{1}{H_0}\int_{\infty}^{z_1} \frac{-1}{E(z)^{\frac{1}{2}}(1+z)}dz$$

Dla modelu desittera Einsteina, tj. $\Omega_m = 1$, $\Omega_{rad} = 0$, $\Omega_k = 0$, $\Omega_\wedge = 0$, równanie wieku wszechświata staje się -

$$t_{age} = \frac{1}{H_0}\int_{0}^{\infty} \frac{1}{(1+z)^{\frac{5}{2}}}dz$$

Po rozwiązaniu całki otrzymujemy -

$$t_H = \frac{2}{3H_0}$$

Nocne niebo jest jak Cosmic Time Machine.Ilekroć obserwujemy odległą planetę, gwiazdę lub galaktykę, widzimy ją taką, jaką było godziny, stulecia, a nawet tysiąclecia temu. Dzieje się tak, ponieważ światło porusza się ze skończoną prędkością (prędkością światła), a biorąc pod uwagę duże odległości we Wszechświecie, nie widzimy obiektów takimi, jakimi są teraz, ale takimi, jakie były, gdy światło zostało wyemitowane. Czas, który upłynął od chwili wykrycia światła tutaj na Ziemi do chwili, gdy zostało ono pierwotnie wyemitowane przez źródło, jest określany jakoLookback Time (t_L(z₁)).

Tak więc okres ważności jest określony wzorem -

$$t_1(z_1) = t_0-t(z_1)$$

Czas podsumowania Wszechświata Desittera Einsteina to -

$$t_L(z) = \frac{2}{3H_0}\left [ 1- \frac{1}{(1+z)^{\frac{3}{2}}} \right ]$$

Punkty do zapamiętania

• Ilekroć obserwujemy odległą planetę, gwiazdę lub galaktykę, widzimy ją taką, jaką było godziny, stulecia, a nawet tysiąclecia temu.

• Czas, który upłynął od momentu wykrycia światła tutaj na Ziemi do momentu wyemitowania go przez źródło, nazywany jest czasem retrospekcji.

W tym rozdziale zrozumiemy, czym jest odległość w średnicy kątowej i jak pomaga w kosmologii.

Dla obecnego wszechświata -

• $\Omega_{m,0} \: = \: 0.3$

• $\Omega_{\wedge,0} \: = \: 0.69$

• $\Omega_{rad,0} \: = \: 0.01$

• $\Omega_{k,0} \: = \: 0$

Do tej pory badaliśmy dwa rodzaje odległości -

• Proper distance (lp) - Odległość, jaką pokonują fotony od źródła do nas, tj Instantaneous distance.

• Comoving distance (lc) - Odległość między obiektami w przestrzeni, która się nie rozszerza, tj. distance in a comoving frame of reference.

Odległość jako funkcja przesunięcia ku czerwieni

Rozważmy galaktykę, która w danym momencie promieniuje fotonem t₁ który jest wykrywany przez obserwatora o godz t₀. Możemy zapisać odpowiednią odległość do galaktyki jako -

$$l_p = \int_{t_1}^{t_0} cdt$$

Niech nastąpi przesunięcie ku czerwieni galaktyki z,

$$\Rightarrow \frac{\mathrm{d} z}{\mathrm{d} t} = -\frac{1}{a^2}\frac{\mathrm{d} a}{\mathrm{d} t}$$

$$\Rightarrow \frac{\mathrm{d} z}{\mathrm{d} t} = -\frac{\frac{\mathrm{d} a}{\mathrm{d} t}}{a}\frac{1}{a}$$

$$\therefore \frac{\mathrm{d} z}{\mathrm{d} t} = -\frac{H(z)}{a}$$

Teraz zbliżająca się odległość galaktyki w dowolnym momencie t będzie -

$$l_c = \frac{l_p}{a(t)}$$

$$l_c = \int_{t_1}^{t_0} \frac{cdt}{a(t)}$$

Jeśli chodzi o z,

$$l_c = \int_{t_0}^{t_1} \frac{cdz}{H(z)}$$

Istnieją dwa sposoby znajdowania odległości, które są następujące:

Zależność strumień-jasność

$$F = \frac{L}{4\pi d^2}$$

gdzie d to odległość u źródła.

Odległość średnicy kątowej źródła

Jeśli znamy rozmiar źródła, jego szerokość kątowa wskaże nam odległość od obserwatora.

$$\theta = \frac{D}{l}$$

gdzie l jest odległością średnicy kątowej źródła.

• θ to rozmiar kątowy źródła.

• D to rozmiar źródła.

Rozważmy galaktykę o rozmiarze D i rozmiarze kątowym dθ.

Wiemy to,

$$d\theta = \frac{D}{d_A}$$

$$\therefore D^2 = a(t)^2(r^2 d\theta^2) \quad \because dr^2 = 0; \: d\phi ^2 \approx 0$$

$$\Rightarrow D = a(t)rd\theta$$

Wymiana pieniędzy r do r_c, zbliżająca się odległość galaktyki, mamy -

$$d\theta = \frac{D}{r_ca(t)}$$

Tutaj, jeśli wybierzemy t = t₀kończymy na pomiarze obecnej odległości do galaktyki. AleDjest mierzona w momencie emisji fotonu. Dlatego przy użyciut = t₀, uzyskujemy większą odległość do galaktyki i stąd niedoszacowanie jej wielkości. Dlatego powinniśmy wykorzystać czast₁.

$$\therefore d\theta = \frac{D}{r_ca(t_1)}$$

Porównując to z poprzednim wynikiem, otrzymujemy -

$$d_\wedge = a(t_1)r_c$$

$$r_c = l_c = \frac{d_\wedge}{a(t_1)} = d_\wedge(1+z_1) \quad \because 1+z_1 = \frac{1}{a(t_1)}$$

W związku z tym,

$$d_\wedge = \frac{c}{1+z_1} \int_{0}^{z_1} \frac{dz}{H(z)}$$

d_A to odległość średnicy kątowej obiektu.

Punkty do zapamiętania

• Jeśli znamy rozmiar źródła, jego szerokość kątowa wskaże nam odległość od obserwatora.

• Właściwa odległość to odległość, jaką pokonują fotony od źródła do nas.

• Dystans w ruchu to odległość między obiektami w przestrzeni, która się nie rozszerza.

Jak omówiono w poprzednim rozdziale, odległość średnicy kątowej do źródła przy przesunięciu ku czerwieni z jest dane przez -

$$d_\wedge (z_{gal}) = \frac{c}{1+z_{gal}}\int_{0}^{z_{gal}} \frac{1}{H(z)}dz$$

$$d_\wedge(z_{gal}) = \frac{r_c}{1+z_{gal}}$$

gdzie $r_c$ zbliża się odległość.

Odległość Luminosity zależy od kosmologii i jest definiowana jako odległość, na której obserwowany strumień f pochodzi z obiektu.

Jeśli wewnętrzna jasność $d_L$ znanego odległego obiektu, możemy obliczyć jego jasność mierząc strumień $f$ który jest określony przez -

$$d_L(z) = \sqrt{\frac{L}{4\pi f}}$$

Energia fotonowa zostaje przesunięta na czerwono.

$$\frac{\lambda_{obs}}{\lambda_{emi}} = \frac{a_0}{a_e}$$

gdzie $\lambda_{obs}, \lambda_{emi}$ są obserwowane i emitowane długości fal i $a_0, a_e$ są odpowiednimi współczynnikami skali.

$$\frac{\Delta t_{obs}}{\Delta t_{emi}} = \frac{a_0}{a_e}$$

gdzie $\Delta_t{obs}$ jest obserwowany jako przedział czasu fotonów, podczas gdy $\Delta_t{emi}$ to przedział czasu, w którym są emitowane.

$$L_{emi} = \frac{nhv_{emi}}{\Delta t_{emi}}$$

$$L_{obs} = \frac{nhv_{obs}}{\Delta t_{obs}}$$

$\Delta t_{obs}$ zajmie więcej czasu niż $\Delta t_{emi}$ ponieważ detektor powinien odbierać wszystkie fotony.

$$L_{obs} = L_{emi}\left ( \frac{a_0}{a_e} \right )^2$$

$$L_{obs} < L_{emi}$$

$$f_{obs} = \frac{L_{obs}}{4\pi d_L^2}$$

W przypadku nierozszerzającego się wszechświata odległość luminancji jest taka sama, jak odległość towarzysząca.

$$d_L = r_c$$

$$\Rightarrow f_{obs} = \frac{L_{obs}}{4\pi r_c^2}$$

$$f_{obs} = \frac{L_{emi}}{4 \pi r_c^2}\left ( \frac{a_e}{a_0} \right )^2$$

$$\Rightarrow d_L = r_c\left ( \frac{a_0}{a_e} \right )$$

Znajdujemy odległość jasności $d_L$ do obliczania jasności emitowanego obiektu $L_{emi}$ -

• Interpretation - Jeśli znamy przesunięcie ku czerwieni z z dowolnej galaktyki, możemy się dowiedzieć $d_A$ iz tego możemy obliczyć $r_c$. Służy do tego, aby się dowiedzieć$d_L$.

• Gdyby $d_L ! = r_c(a_0/a_e)$, to nie możemy znaleźć Lemiego od $f_{obs}$.

Zależność między odległością jasności $d_L$ i odległość średnicy kątowej $d_A.$

Wiemy, że -

$$d_A(z_{gal}) = \frac{d_L}{1+z_{gal}}\left ( \frac{a_0}{a_e} \right )$$

$$d_L = (1 + z_{gal})d_A(z_{gal})\left ( \frac{a_0}{a_e} \right )$$

Współczynnik skali, gdy emitowane są fotony, jest wyrażony wzorem -

$$a_e = \frac{1}{(1+z_{gal})}$$

Współczynnik skali dla obecnego wszechświata wynosi -

$$a_0 = 1$$

$$d_L = (1 + z_{gal})^2d_\wedge(z_{gal})$$

Który wybrać $d_L$ lub $d_A$?

• A zatem dla galaktyki o znanej wielkości i przesunięciu ku czerwieni do obliczenia jej wielkości $d_A$ jest używany.

• Jeśli istnieje galaktyka o danej pozornej wielkości, to aby dowiedzieć się, jaka jest duża, $d_L$ jest używany.

Example - Jeśli podano, że dwie galaktyki o równym przesunięciu ku czerwieni (z = 1) iw płaszczyźnie nieba są oddzielone 2.3 arc sec więc jaka jest maksymalna fizyczna separacja między tymi dwoma?

W tym celu użyj $d_A$ w następujący sposób -

$$d_A(z_{gal}) = \frac{c}{1+z_{gal}}\int_{0}^{z_{gal}} \frac{1}{H(z)}dz$$

gdzie z = 1 zastępuje H (z) w oparciu o kosmologiczne parametry galaktyk.

Punkty do zapamiętania

• Odległość świetlna zależy od cosmology.

• Jeśli wewnętrzna jasność $d_L$ znanego odległego obiektu, możemy obliczyć jego jasność mierząc strumień f.

• W przypadku nierozszerzającego się wszechświata odległość jasności jest taka sama jak comoving distance.

• Odległość jasności jest zawsze większa niż Angular Diameter Distance.

Dla dowolnego przesunięcia ku czerwieni (z) mamy dwie wartości odległości -

• Odległość średnicy kątowej (d _A )
• Jasność Odległość (d _L )

Nie ma jednej definicji „kosmologicznej” odległości we wszechświecie. Wybór odległości zależy od celu i wygody aplikacji.

Aby przetestować przewidywany trend zmiany rozmiaru kątowego obiektu wraz z przesunięciem ku czerwieni, potrzebna jest miara standardowego rozmiaru na niebie. Powinien to być przedmiot, który -

• jest bardzo świecący, więc można go wykryć przy z> 1.

• jest bardzo duży, więc możemy rozwiązać jego rozmiar kątowy.

• nie ewoluował morfologicznie w czasie istotnym kosmologicznie (z ∼ 1 odpowiada czasowi wstecznemu około 7 Gyr).

Niektóre obiekty (np. Galaktyki cD) spełniają dwa pierwsze kryteria. Jednak prawie każdy obiekt ewoluuje morfologicznie w czasie. Ogólnie rzecz biorąc, obiekty astrofizyczne (rozszerzone źródła) wydają się być z natury mniejsze w przeszłości, ponieważ wciąż się formują.

Jasność Odległość

Odległość jasności zależy od kosmologii. Zależność odległości świetlnej od kosmologii sprawia, że ​​jest to użyteczna miara parametrów kosmologicznych.

Parametry kosmologiczne można oszacować, jeśli znajdziemy standardową świecę, która nie ewoluuje samoistnie i istnieje od wszechświata lokalnego do wysokiego przesunięcia ku czerwieni.

Standardowa świeca to taka, która nie różni się swoją jasnością w zależności od źródła. Założenie jest takie, że każda różnica w szacowanej jasności standardowych świec musi wynikać z kosmologii. Jedną z takich świec jest supernowa typu Ia.

Supernowe typu 1a (SNe)

Są one wynikiem eksplozji białego karła po wystarczającej akrecji masy od jego towarzysza, czerwonego olbrzyma lub podobnej gwiazdy ciągu głównego, w układzie podwójnym. Gdy czerwony olbrzym zbliży się do odległości płata Roche'a Białego karła, rozpoczyna się transfer masy i ostatecznie biały karzeł eksploduje, wydzielając ogromną ilość energii, nie pozostawiając żadnego rdzenia. Są to tzw. Supernowe typu 1a. Typowa szybkość eksplozji supernowych typu 1a w galaktyce wynosi 1 na wiek.

Poszukiwania typu 1a SNe trwają z różnymi zespołami -

• High z Supernova Search Team (Brian Schmidt, Adam Reiss i wsp.)
• Projekt kosmologii Supernova (Saul Perlmutter et al.)

Był inny zespół badawczy o nazwie Carnegie Supernovae Project który dał podobne wyniki.

Podobieństwo wyników różnych zespołów wskazuje na kosmologiczny charakter SNe typu 1a. Stąd są to wydajne standardowe świece.

Punkty do zapamiętania

• Nie ma jednej definicji „kosmologicznej” odległości we wszechświecie.

• Najczęściej używane są odległości średnicy kątowej i odległości jasności.

• Standardowa świeca to taka, która nie różni się swoją jasnością w zależności od źródła.

• Typ 1a SNe spełnia kryteria standardowej świecy.

CMB (kosmiczne tło mikrofalowe) zasadniczo składa się z fotonów z czasu, gdy materia i promieniowanie były w równowadze. W latach dwudziestych XX wieku idea rozszerzającego się wszechświata została zaakceptowana i mogła odpowiedzieć na kilka pytań. Ale pytania o obfitość cięższych pierwiastków i obfitość pozostały bez odpowiedzi. Co więcej, rozszerzający się wszechświat oznaczał, że gęstość materii powinna spaść do 0.

W 1948 roku George Gammow i Ralph Alpher wyjaśnili pochodzenie cięższych pierwiastków i ich obfitość za pomocą „Wielkiego Wybuchu”. Wraz z Robertem Hermanem przepowiedzieli istnienie „Reliktowego promieniowania”, czyli promieniowania pozostałego po „Wielkim Wybuchu”. Przewidywana temperatura tego pozostałego promieniowania wynosiła 50-6 K. W 1965 roku Robert Dicke, Jim Peebles i David Wilkinson wraz z grupą badawczą Amo Periziasa eksperymentalnie wykryli CMB.

Wczesny wszechświat był bardzo gorący, a energia była zbyt wysoka, aby materia pozostała neutralna. Stąd materia była w zjonizowanej formie -Plasma. Promieniowanie (fotony) i materia (plazma) oddziałują głównie poprzez następujące trzy procesy.

• Compton Scattering - (Główny proces interakcji) Nieelastyczne rozpraszanie między fotonem o wysokiej energii i cząstką naładowaną o niskiej energii.

• Thomson Scattering - Elastyczne rozpraszanie fotonu przez swobodnie naładowaną cząstkę.

• Inverse Compton Scattering- Naładowana cząstka o wysokiej energii i foton o niskiej energii. Te interakcje ostatecznie doprowadziły do ​​tego, że materia i promieniowanie znalazły się w równowadze termicznej.

Równowaga termiczna

W równowadze termicznej promieniowanie jest zgodne z Planck Distribution of Energy,

$$B_v(T) = \frac{2hv^3}{c(e^{hv/k_BT}-1)}$$

W tym czasie, ze względu na bardzo częste oddziaływania, średnia droga swobodna fotonów była bardzo mała. Wszechświat był nieprzejrzysty dla promieniowania. Wczesny wszechświat był zdominowany przez promieniowanie. Wszechświat ewoluował w taki sposób, że materia i promieniowanie osiągnęły równowagę termiczną, a ich gęstość energii stała się równa. Można to zobaczyć na wykresie przedstawiającym ewolucję gęstości wraz ze współczynnikiem skali. Znajdźmy współczynnik skali (czas) (a (t)), w którym materia i promieniowanie osiągnęły równowagę.

$$\rho_m \propto \frac{1}{a^3}, \: \rho_r \propto \frac{1}{a^4}$$

$$\frac{\rho_{m,t}}{\rho_{r,t}} = \frac{\Omega_{m,t}}{\Omega_{r,t}} = \frac{\Omega_{m,0}}{\Omega_{r,0}}a(t)$$

W równowadze

$$\frac{\rho_{m,t}}{\rho_{r,t}} = \frac{\Omega_{m,t}}{\Omega_{r,t}} = 1$$

$$\Rightarrow \frac{\Omega_{m,0}}{\Omega_{r,0}}a(t) = 1 \: \Rightarrow a(t) = 2.96 \times 10^{-4}$$

za pomocą $\Omega_{m,0} = 0.27$ i $\Omega_{r,0} = 8 \times 10^{−5}$. Przesunięcie ku czerwieni odpowiadające temu współczynnikowi skali jest określone przez -

$$z = 1/a(t)-1 \approx 3375$$

Gęstość energii promieniowania spadła z powodu rozszerzania się wszechświata. W ten sposób wszechświat zaczął się ochładzać. Gdy energia fotonów zaczęła spadać, zaczęły się formować neutralne atomy. W ten sposób około 1300 roku zaczął się formować obojętny wodór. W tej epoce panowała temperatura bliska 3000K.

Interakcja między materią a promieniowaniem stała się bardzo rzadka, w związku z czym wszechświat stał się przezroczysty dla promieniowania. Ten okres czasu nazywa się“Surface of last scattering”ponieważ średnia droga swobodna fotonów stała się bardzo duża, przez co po tym okresie prawie nie nastąpiło rozproszenie. Nazywa się to również jako“Cosmic Photosphere”.

Punkty do zapamiętania

• KMPT tworzą fotony z czasu, gdy materia i promieniowanie były w równowadze.

• Wczesny wszechświat był bardzo gorący, a energia była zbyt wysoka, aby materia pozostała neutralna, więc istniał jako materia zjonizowana - Plazma.

• Rozpraszanie Comptona, Thomsona i odwrotnego rozpraszania Comptona były wówczas trzema procesami interakcji materia-promieniowanie.

• Wszechświat ewoluował w taki sposób, że materia i promieniowanie osiągnęły równowagę termiczną.

Najpierw powinniśmy zrozumieć, co charakteryzuje plik decoupling. Wiemy, że energie były znacznie wyższe do tego stopnia, że ​​materia istniała tylko w postaciIonized Particles. Zatem w epokach odsprzęgania i rekombinacji energia musiała spaść, aby umożliwić jonizację wodoru. Można dokonać przybliżonych obliczeń w celu oszacowania temperatury w czasie odsprzęgania.

Wykonano to w następujący sposób -

Po pierwsze, rozważmy tylko jonizację wodoru w stanie podstawowym.

$$hv \approx k_BT$$

$$\therefore T \approx \frac{hv}{k_B}$$

Do jonizacji wodoru w stanie podstawowym, hν wynosi 13,6 eV i kB jest Boltzmann Constant8,61 × ^10-5 eV / K, co oznacza, że ​​temperatura wynosi 1,5 × 105 kelwinów.

To zasadniczo mówi nam, że jeśli temperatura spadnie poniżej 1,5 × 10 ⁵ K, neutralne atomy mogą zacząć się formować.

Wiemy, że stosunek fotonów do barionów wynosi około 5 × 10 ¹⁰ . Dlatego nawet na końcu wykresu, gdzie liczba fotonów maleje, nadal będzie wystarczająco dużo fotonów, aby zjonizować atomy wodoru. Ponadto rekombinacja elektronu i protonu nie gwarantuje atomu wodoru w stanie podstawowym. Stany wzbudzone wymagają mniejszej energii do jonizacji. Stąd zdyscyplinowana analiza statystyczna powinna być przeprowadzana indywidualnie dla każdego przypadku, aby uzyskać dokładną wartość. Obliczenia ustalają temperaturę na około 3000K.

Dla wyjaśnienia rozważymy przypadek wzbudzenia wodoru w pierwszym stanie wzbudzonym. Ogólne wyrażenie na stosunek liczby fotonów do energii większej niżΔE, Nγ (> ΔE) do całkowitej liczby fotonów Nγ jest dane przez -

$$\frac{N_\gamma(> \Delta E)}{N_\gamma} \propto e^{\frac{-\Delta E}{kT}}$$

W przypadku wzbudzenia wodoru do pierwszego stanu wzbudzonego, ΔEwynosi 10,2 eV. Teraz, jeśli weźmiemy pod uwagę bardzo konserwatywną liczbę co najmniej 1 fotonu o energii większej niż 10,2 na każdy barion (pamiętając, że stosunek wynosi 5 × 10 ¹⁰ , otrzymamy temperaturę z równania 3 jako 4800 K (wstawione Nγ (> ΔE) = Np).

Jest to temperatura potrzebna do stworzenia populacji neutralnych atomów wodoru w pierwszym stanie wzbudzonym. Temperatura jonizacji jest znacznie niższa. W ten sposób uzyskujemy oszacowanie lepsze niż 1,5 × 10 ⁵ K, czyli bliższe przyjętej wartości 3000 K.

Zależność między przesunięciem ku czerwieni a temperaturą

Aby zrozumieć związek między przesunięciem ku czerwieni a temperaturą, stosujemy następujące dwie metody opisane poniżej.

Metoda 1

Od Wien’s Law, wiemy to

$$\lambda_mT = constant$$

Aby odnieść to do przesunięcia ku czerwieni, używamy -

$$1+z = \frac{\lambda_0}{\lambda_e}$$

Tak jak $λ_oT_o = λ_eT(z)$otrzymujemy -

$$T(z) = T_0\frac{\lambda_0}{\lambda_e} = T_0(1+z)$$

Oprawa T_o jako aktualna wartość 3K możemy otrzymać wartości temperatury dla danego przesunięcia ku czerwieni.

Metoda 2

Jeśli chodzi o częstotliwość, wiemy -

$$v_0 = \frac{v_e}{1+z}$$

$$B_vdv = \frac{2hv^3}{c^2} \frac{dv}{e^{hv/kT}-1}$$

To mówi nam o energii netto fotonów dla przedziału energii i hνjest energią pojedynczego fotonu. Stąd możemy otrzymać liczbę fotonów wgBνdν/hν.

Gdyby $n_{νo}$ jest na prezent i $n_{νe}$ za wyemitowane otrzymujemy -

$$\frac{n_{v_e}}{n_{v_0}} = (1+z)^3$$

Po uproszczeniu otrzymujemy:

$$n_{v_0} =\frac{2v_c^2}{c^2}\frac{dv_c}{e^{hv/kT}-1}\frac{1}{(1+z)^3}=\frac{2v_0^2}{c^2}\frac{dv_c}{e^{hv/kT}-1}$$

To daje nam Wien’s Law ponownie i stąd można wywnioskować, że -

$$T(z) = T_0\frac{\lambda_0}{\lambda_e} = T_0(1+z)$$

Punkty do zapamiętania

• Wczesny wszechświat był bardzo gorący, ∼ 3000K.
• Obecne pomiary pokazują, że temperatura Wszechświata jest bliska 3K.
• Im dalej cofamy się w czasie, tym temperatura rośnie proporcjonalnie.

W tym rozdziale omówimy anizotropię promieniowania CMB i COBE, czyli Cosmic Background Explorer.

Pierwotne anizotropie w KMPT

Aby zrozumieć obserwacje z kosmosu i pierwotne anizotropie w kosmicznym mikrofalowym promieniowaniu tła, weźmy następujące równania i zrozummy je, jak pokazano poniżej.

Gęstość liczby fotonów CMB (n _γ , 0)

$$n_{\gamma,0} = \frac{Total \: energy \: density}{Characteristic \: energy \:of \:Photons}$$

$$n_{\gamma,0} = \frac{aT_0^4}{k_BT_0}$$

Gdzie $k_B$ jest Boltzmann Constant i $T_0$ jest present temperature of the universe.

Używając aktualnej temperatury $(T_0)$jako 2,7 K otrzymujemy aktualną gęstość liczby fotonów CMB jako 400 cm ^-3 .

Gęstość liczby fotonów w kosmosie jest znacznie mniejsza (∼ = ^10-3 cm ^-3 ) w dużych skalach.

Stosunek barionu do fotonu (η)

Jeśli udział gwiazd z galaktyk, które miesza się z KMPT, jest znikomy, stosunek barionu do protonu wynosi -

$$\eta = \frac{n_{b,0}}{n_{\gamma,0}}$$

Bieżąca wartość to ∼5 × ^10-10 . Ponieważ zarówno gęstości liczbowe fotonów, jak i liczb barionowych są proporcjonalne doa⁻³, następnie η nie ewoluuje z czasem.

Gęstość energii

W przeciwieństwie do gęstości liczbowej, gęstość energii materii jest obecnie bardziej zdominowana niż gęstość energii fotonów.

Gęstość energii materii barionowej = $\rho_{b,0}c^2 = 0.04\rho_cc^2 = 2 × 10^{−9} ergcm^{−3}$. Podczas gdy gęstość energii promieniowania =$aT_0^4 = 4 \times 10^{−13}ergcm{−3}$.

Izotropia promieniowania KMPT

Penzias i Wilsonstwierdził, że KMPT jest izotropowy w granicach obserwacji. Ograniczenia to niska rozdzielczość kątowa i czułość instrumentów. Prowadzili obserwacje z Ziemi, z tego powodu obserwacje nie mogą być prowadzone w całym widmie, ponieważ para wodna w atmosferze pochłania wiele długości fal w zakresie od 1 mm do 1 m. Tak więc CMB nie może być traktowane jako widmo.

Uważa się, że CMB jest niezmienna rotacyjnie (izotropowa). Ponieważ istniał czas, w którym materia i promieniowanie były w równowadze, formowanie się struktur we Wszechświecie jest niewytłumaczalne. Ponieważ rozkład materii nie jest izotropowy, ale jest zlepiony razem jak kosmiczna sieć z ogromnymi pustkami pomiędzy nimi, uważa się, że CMB ma pochodzenie pozagalaktyczne.

Ale gdy rozpoczęły się obserwacje z kosmosu, znaleziono anizotropie w KMPT, co prowadzi do wniosku, że te anizotropie w materii prowadzą do powstania struktur.

Obserwacja promieniowania KMPT z kosmosu

Główne satelity, które zostały wystrzelone w celu obserwacji KMPT to:

• Cosmic Microwave Background Explorer (COBE, 1989)

• Wilkinson Microwave Anisotropy Probe (WMAP, 2001) i

• Planck (2009).

COBE (kosmiczna eksploracja tła)

COBE posiadała głównie dwa instrumenty. ByliFar InfraRed Absolute Spectrometer (FIRAS) i Differential Microwave Radiometers(Anteny DMR). FIRAS mierzy intensywność CMB jako funkcję długości fali wzdłuż dowolnego określonego kierunku. Natomiast DMR ma 3 anteny do pomiaru różnicy intensywności KMPT z trzech różnych kierunków. Poniższe wskazówki dają nam więcej informacji na temat FIRAS i DMR.

• Obserwacje CMB z FIRAS pokazują, że promieniowanie KMPT odpowiada widmowi ciała doskonale czarnego przy T = 2,72528 ± 0,00065 K.

• DMR mierzy trzy częstotliwości (31,5 GHz, 53 GHz, 90 GHz) we wszystkich kierunkach na niebie.

• „Czerwony symbol Batmana” w obserwacjach DMR to szum z emisji pierwszego planu (galaktyczna rozproszona emisja synchrotronowa).

• Zmiany intensywności w obserwacjach odpowiadają zmianom temperatury. Obecność miejsc gorących i zimnych świadczy o tym, że promieniowanie KMPT jest anizotropowe.

• Ta anizotropia musi występować w czasie odsprzęgania, ponieważ nie ma żadnych zniekształceń w KMPT. Zatem materia powinna mieć niektóre kieszenie o większej gęstości niż inne.

Wyniki COBE

Widmo KMPT (intensywność jako funkcja energii) to prawie idealne ciało czarne, odpowiadające T = 2,7 K. Specyficzna intensywność promieniowania KMPT jest prawie taka sama we wszystkich kierunkach. Potwierdzenie, że wszechświat jest izotropowy w dużej skali (potwierdza nasze założenie o zasadzie kosmologicznej).

Analiza danych wykazała, że ​​istnieją anizotropie temperatury („fluktuacje”) w widmie KMPT przy rozdzielczości COBE (DMR).

Resolution of COBE, WMAP, Planck

• Instrument DMR na pokładzie COBE miał ograniczającą (maksymalną) rozdzielczość przestrzenną ∼ 7 stopni.

• Wilkinson Microwave Anisotropy Probe (WMAP) miała średnią rozdzielczość ∼ 0,7 stopnia.

• Satelita Planck ma rozdzielczość kątową ∼ 10 minut łuku.

Punkty do zapamiętania

• Gęstość liczby fotonów w kosmosie jest znacznie mniejsza niż gęstość liczby fotonów w KMPT.

• Żyjemy we wszechświecie zdominowanym przez materię, ponieważ gęstość energii materii jest wyższa niż gęstość energii fotonów.

• COBE, WMAP, Planck to wysiłki zmierzające do pomiaru i kwantyfikacji anizotropów w CMB.

• Tworzenie struktury we wszechświecie jest wynikiem anizotropii KMPT.

Kiedy patrzymy na dopracowaną, poprawioną mapę KMPT całego nieba, widać dużo zanieczyszczeń pierwszego planu, co jest rodzajem anisotropyna tych mapach. Widzimy, że te emisje na pierwszym planie pochodzą z galaktyki Drogi Mlecznej. Intensywność KMPT jest wysoka wzdłuż płaszczyzny galaktycznej i zmniejsza się, gdy się oddalamy. W nich możemy zaobserwować wtórne anizotropie, czyli emisje synchrotronowe z galaktyki. Te emisje stanowią zanieczyszczenie pierwszego planu. Aby spojrzeć na emisję KMPT z nieba, musimy odjąć te emisje na pierwszym planie.

Poniższy obraz przedstawia CMB z emisjami na pierwszym planie.

Anizotropia dipolowa

Istnieje inny rodzaj anizotropii, który został znaleziony na mapie całego nieba KMPT, nazywany anizotropią dipolową. Nie jest to związane z wczesnym wszechświatem. Można to przedstawić za pomocą sferycznych funkcji harmonicznych. Jeśli na powierzchni kulistej znajduje się wzór i chcemy go odwzorować za pomocą funkcji matematycznych, możemy to zrobić za pomocą funkcji trygonometrycznych. Więc kiedy mapujemy, może to być monopol - taki sam w każdym kierunku lub dipol - odwraca właściwości po obróceniu o 180 stopni. Podobnie mamy kwadrupol i tak dalej. W przypadku złożonego wzoru można go wyrazić jako sumę tych monopoli, dipoli, kwadrupoli itp.

KMPT jest modelowany w taki sposób, że jednym z głównych źródeł anizotropii na mapie całego nieba jest anizotropia dipolowa, ale nie jest to pierwotne modelowanie KMPT. Można to zobaczyć na poniższym obrazku.

Kierunek dipola, który widzimy, nie jest żadnym przypadkowym kierunkiem. Anizotropia dipolowa ma kierunek. Widzimy intensywność KMPT wzdłuż określonego kierunku. Kierunek ten wynika z wektora prędkości Układu Słonecznego. Prędkość Ziemi można przedstawić w odniesieniu do słońca lub środka galaktyki. Kierunek, w którym porusza się Ziemia, obserwujemy przesunięcie ku niebieskiemu i przesunięcie ku czerwieni, a dipol leży w tym kierunku.

Powyższe zdjęcie ma typowy wygląd dipolowy, ponieważ nasza Galaktyka porusza się w określonym kierunku. W rezultacie jedna strona nieba będzie wyglądać na przesuniętą do czerwieni, a po drugiej stronie z przesunięciem do niebieskiego. W tym przypadku przesunięcie ku czerwieni oznacza, że ​​fotony mają dłuższą długość fali = chłodniejszą (więc odwrotnie od ich nazwy, na powyższym diagramie wyglądają na niebieskie).

Można powiedzieć, że w danej chwili Ziemia porusza się w określonym kierunku względem słońca / centrum galaktyki / KMPT na niebie. Wtedy, jeśli spojrzymy pod dowolnym kątem i zmierzymy temperaturę dla KMPT, byłoby inaczej. Dzieje się tak, ponieważ mierzymy fotony, które są przesunięte do niebieskiego lub do czerwieni i zależą od linii widzenia fotonów na niebie.

Punkty do zapamiętania

• Zanieczyszczenie pierwszego planu na mapie całego nieba KMPT nazywa się anizotropią KMPT.

• Te emisje pochodzą z naszej własnej galaktyki Drogi Mlecznej.

• Dwa typy anizotropów to: anizotropia dipolowa i anizotropia widma mocy kątowej.

• Anizotropia dipolowa przebiega w określonym kierunku, podczas gdy anizotropia kątowego spektrum mocy rozprzestrzenia się wszędzie.

Długość horyzontu to odległość pokonana przez fotony światła od „Wielkiego Wybuchu” do „Ery Rekombinacji”. W 1 ^st pik kątowego widma w θ = 1◦ (L = 180), który jest szczególnym skali długości.

Właściwa odległość między dwoma punktami jest określona wzorem -

$$r_p = \int_{0}^{t}cdt$$

Kiedy weźmiemy przedział czasu od t = 0 do t = t _rec , to

$$r_H = \int_{0}^{t_{rec}}cdt$$

Gdzie $r_H$ to właściwa odległość horyzontu.

Teraz wiemy, że -

$$\dot{a} = \frac{\mathrm{d} a}{\mathrm{d} t}$$

$$dt = \frac{da}{\dot{a}}$$

Gdy t = 0, a = 0.

Następnie $t = t_{rec}, a = a_0 / (1 + z_{rec})$.

Dlatego możemy napisać

$$r_H(z_{rec})=\int_{0}^{a_{rec}} c\frac{da}{aH}$$

$$H(a_{rec}) = H(z_{rec}) = H_0\sqrt{\Omega_{m,0}}a^{-3/2}$$

Podczas Recombination period universebyła zdominowana przez materię. to znaczy,Ωrad << Ωmatter. Dlatego termin promieniowanie zostaje odrzucony.

$$r_H(z_{rec}) = \frac{c}{H_0\sqrt{\Omega_{m,0}}}\int_{0}^{a_{rec}} \frac{da}{a^{-1/2}}$$

$$r_H(z_{rec}) = \frac{2c}{3H_0\sqrt{\Omega_{m,0}}}\frac{1}{(1+z_{rec})^{3/2}}$$

$$\theta_H(rec) = \frac{r_H(z_{rec})}{d_A(z_{rec})}$$

Co jest równe 0,5 stopnia, jeśli umieścimy wszystkie znane wartości w równaniu.

Plik Electromagnetic radiationjest matowy od powierzchni ostatniego rozproszenia. Jakiekolwiek dwa punkty „nie” leżące w horyzoncie siebie nawzajem nie muszą mieć takich samych właściwości. Więc da różne wartości temperatury.

Na tej powierzchni możemy uzyskać dwa punkty, które nie przecinały się ze sobą, co oznacza, że ​​w pewnym momencie Wszechświat rozszerzał się szybciej niż prędkość światła, co jest inflacyjnym modelem ekspansji.

Punkty do zapamiętania

• Długość horyzontu to odległość pokonana przez fotony światła od „Wielkiego Wybuchu” do „Ery Rekombinacji”.

• W okresie Rekombinacji wszechświat był zdominowany przez materię.

• Promieniowanie elektromagnetyczne jest matowe od powierzchni ostatniego rozproszenia.

Astrobiologyto badanie pochodzenia, ewolucji, rozmieszczenia i przyszłości życia we wszechświecie. Zajmuje się wykrywaniem i wykrywaniemExtrasolar Planets.

Astrobiology odnosi się do następujących punktów -

• Jak zaczyna się i ewoluuje życie? (biologia + geologia + chemia + nauki o atmosferze)

• Czy istnieją światy poza Ziemią, które sprzyjają życiu? (astronomia)

• Jaka będzie przyszłość życia na ziemi?

Astronomy odnosi się do następujących punktów -

• Jak wykryć układ planetarny wokół innych gwiazd?

• Jedną z metod jest bezpośrednie obrazowanie, ale jest to bardzo trudne zadanie, ponieważ planety są wyjątkowo słabymi źródłami światła w porównaniu z gwiazdami, a to, co pochodzi z nich, ma tendencję do gubienia się w blasku ich gwiazdy macierzystej.

• Kontrast jest lepszy, gdy planeta znajduje się bliżej swojej gwiazdy macierzystej i jest gorąca, dzięki czemu emituje intensywne promieniowanie podczerwone. Możemy robić zdjęcia w podczerwieni.

Techniki pozasłonecznego wykrywania planet

Najskuteczniejsze techniki wykrywania planet pozasłonecznych są następujące. Każdy z nich został również szczegółowo wyjaśniony w kolejnych rozdziałach.

Metoda prędkości radialnej

Nazywa się ją również metodą Dopplera. W tym -

• Układ planet gwiezdnych obraca się wokół ich centrum bariery, gwiazda się chwieje.

• Kołysanie można wykryć za pomocą

  • Okresowe zmiany koloru czerwonego / niebieskiego. Astrometria - bardzo precyzyjny pomiar obiektów na niebie.

Metoda tranzytu

Aby ustalić rozmiar, zastosowano metodę tranzytu (teleskop kosmiczny Keplera). Spadek jasności gwiazdy na planetę jest zwykle bardzo mniejszy, w przeciwieństwie do układu podwójnego.

Obrazowanie bezpośrednie

Obrazowanie planety za pomocą teleskopu.

Przyjrzyjmy się studium przypadku wykonanemu przy użyciu metody prędkości radialnej.

Studium przypadku

To studium przypadku dotyczy orbity kołowej i płaszczyzny orbity prostopadłej do płaszczyzny nieba. Czas potrzebny obojgu dookoła centrum barowego będzie taki sam. Będzie równa różnicy czasu między dwoma przesunięciem ku czerwieni lub przesunięciem w kierunku niebieskim.

Rozważ następujący obraz.

W A i C - mierzona jest pełna prędkość. W C prędkość wynosi zero.

• Vrmax = V _* to prawdziwa prędkość gwiazdy.

• P jest okresem gwiazdy i planety.

• θ to faza orbity.

• Masa gwiazdy - M _* , promień orbity a _* , masa planetym_p.

Z równania środka masy,

$$m_p a_p = M_\ast a_\ast$$

Z równania prędkości

$$V_\ast = \frac{2\pi a_\ast}{P}$$

$$\Rightarrow a_\ast = \frac{PV_\ast}{2\pi}$$

Od Kepler’s Law,

$$P^2 = \frac{4\pi^2a_p^3}{GM_\ast}$$

$$\Rightarrow a_p = \left ( \frac{P^2GM_\ast}{4\pi^2} \right)^{1/3}$$

Z powyższych równań otrzymujemy -

$$\Rightarrow m_p = \left( \frac{P}{2\pi G} \right)^{1/3}M_\ast^{2/3}V_\ast$$

Otrzymujemy: $m_p, a_p$ i $a_\ast$.

Powyższe równanie dotyczy większości masywnych planet w pobliżu gwiazdy.

Punkty do zapamiętania

• Astrobiologia to nauka o pochodzeniu, ewolucji, dystrybucji i przyszłości życia we wszechświecie.

• Techniki wykrywania planet pozasłonecznych to: metoda prędkości radialnej, metoda tranzytu, obrazowanie bezpośrednie itp.

• Wobbling można wykryć za pomocą okresowych przesunięć czerwonego / niebieskiego i astrometrii.

• Metoda prędkości radialnych jest ukierunkowana na wykrywanie masywnych planet w pobliżu gwiazdy.

W poprzednim rozdziale omówiono metodę prędkości radialnej dla przypadku, w którym płaszczyzna orbity i płaszczyzna nieba są prostopadłe dla orbit kołowych. Tutaj mamy do czynienia z jeszcze jednym przypadkiem, kiedy płaszczyzna orbity i płaszczyzna nieba nie są prostopadłe dla orbit kołowych.

Gdy płaszczyzna orbity jest ustawiona pod kątem do płaszczyzny nieba (nie prostopadle), mamy następującą sytuację -

W tym przypadku, gdy były prostopadłe, mieliśmy dwa punkty, w których mogliśmy zmierzyć prawdziwą prędkość. Ale tutaj nie jest to możliwe. We wszystkich punktach możemy zmierzyć tylko składową prawdziwej prędkości,v.

$$v_r = v \:sin(i)cos(\theta)$$

gdzie θjest fazą orbity, która jest wielkością zależną od czasu. Kąt nachyleniaiz drugiej strony jest niezależny od czasu. W związku z tym,

$$(v_r)_{max} = v\: sin(i)$$

Obserwowana krzywa prędkości radialnej będzie miała następującą postać -

Kiedy płaszczyzna orbity jest prostopadła do nieba -

$$m_p = \left ( \frac{P}{2\pi G} \right )^{\frac{1}{3}}(M_\ast)^{\frac{2}{3}}v$$

gdzie m_p, P, G, M∗to masa planety, okres orbitalny, uniwersalna stała grawitacyjna i masa gwiazdy. Ale w tym przypadku powinniśmy zmodyfikować to w następujący sposób -

$$m_psin(i) = \left ( \frac{P}{2\pi G} \right )^{\frac{1}{3}} (M_\ast)^{\frac{2}{3}}(v_r)_{max}$$

Ale znalezienie wartości i jest trudnym zadaniem. Możemy nałożyć pewne ograniczenia na wartośćiprzy użyciu metody tranzytu. Przejście planety między gwiazdą a Ziemią nazywa się tranzytem. Możemy uzyskać krzywą blasku obserwując przejście, a znaczny spadek obserwowanego strumienia krzywej blasku oznacza, że ​​i jest bliskie 90 stopni. Jeśli takie warunki nie są spełnione, nie możemy mieć pojęcia o wartościi. Następnie wartośćm_p znalezione przez nas może służyć jako dolna granica masy planety, ponieważ tak jest w rzeczywistości m_p sin(i) i sin(i) ≤ 1.

Podsumowując, metoda prędkości radialnej jest wygodniejsza niż metoda tranzytu, ponieważ prędkość radialną można zmierzyć w dowolnym momencie, ale pomiary przejścia można wykonać tylko podczas tranzytu, który może nie trwać długo.

Punkty do zapamiętania

• Znalezienie nachylenia orbity planety nie jest osiągane metodą Radial Velocity.

• Metoda prędkości radialnej jest lepsza niż metoda tranzytu, ponieważ prędkość radialną można zmierzyć zawsze w przeciwieństwie do tranzytów.

• Tranzyty są krótkotrwałe i bardzo łatwe do przeoczenia.

Metoda tranzytu (Kepler Space Telescope)służy do określenia rozmiaru. Spadek jasności gwiazdy przez planetę jest zwykle mniejszy od układu podwójnego.

• F₀ to strumień gwiazdy, zanim planeta ją zakryje.

• F₁ to strumień po tym, jak cała planeta znajdzie się przed gwiazdą.

Poniższy obraz zostanie użyty do wszystkich obliczeń.

$$\frac{F_0 - F_1}{F_0} = \frac{\pi r_p^{2}}{\pi R^2_\ast}$$

$$\frac{\Delta F}{F} \cong \frac{r^2_p}{R^2_\ast}$$

$$\left ( \frac{\Delta F}{F} \right )_{earth} \cong 0.001\%$$

$$\left ( \frac{\Delta F}{F} \right )_{jupiter} \cong 1\%$$

Nie jest to łatwe do osiągnięcia za pomocą teleskopu naziemnego. Osiąga to teleskop Hubble'a.

Tutaj, $t_T$ to czas między pozycjami A i D i $t_F$ to czas między pozycjami B i C.

Geometria przejścia związana z nachyleniem isystemu. Szerokość geograficzna i nachylenie tranzytu są wymienne.

Z powyższych zdjęć możemy napisać -

$$\frac{h}{a} = cos(i)$$

$$\frac{h}{R_\ast} = sin(\delta)$$

$$cos(i) = \frac{R_\ast sin(\delta)}{a}$$

$$y^2 = (R_\ast + R_p)^2 - h^2$$

$$y = [(R_\ast + R_p)^2 - h^2]^{\frac{1}{2}}$$

$$sin(\theta) = \frac{y}{a}$$

$$\theta = sin^{-1}\left [ \frac{(R_\ast + R_p)^2 - a^2cos^2(i)}{a^2} \right ]^{\frac{1}{2}}$$

$$t_T = \frac{P}{2\pi} \times 2\theta$$

Tutaj, $t_T$ jest ułamkiem okresu, w którym zachodzi tranzyt, a (2θ / 2π) jest ułamkiem kąta, dla którego zachodzi tranzyt.

$$sin(\frac{t_T\pi}{P}) = \frac{R_\ast}{a}\left [ \left ( 1+ \frac{R_p}{R_\ast}\right )^2 - \left ( \frac{a}{R_\ast}cos(i)\right )^2 \right ]^{\frac{1}{2}}$$

Zwykle >> R ∗ >> Rp. Więc możemy napisać -

$$sin(\frac{t_T\pi}{P}) = \frac{R_\ast}{a}\left [ 1- \left ( \frac{a}{R_\ast}cos(i) \right )^2\right ]^{\frac{1}{2}}$$

Tutaj, Pto czas trwania między dwoma kolejnymi tranzytami. Czas przejścia jest znacznie krótszy w porównaniu z okresem orbitalnym. W związku z tym,

$$t_T = \frac{P}{\pi}\left [ \left ( \frac{R_\ast}{a}\right )^2 - cos^2(i)\right ]^{\frac{1}{2}}$$

Tutaj, t_T, P, R∗ są obserwowalne, a i i należy się dowiedzieć.

Teraz,

$$sin(\frac{t_F\pi}{P}) = \frac{R_\ast}{a}\left [\left (1 - \frac{R_p}{R_\ast} \right )^2 - \left ( \frac{a}{R_\ast}cos\:i \right )^2\right ]^{\frac{1}{2}}$$

gdzie, $y^2 = (R_\ast − R_p)^2 − h^2$.

Pozwolić,

$$\frac{\Delta F}{F} = D = \left ( \frac{R_p}{R_\ast} \right )^2$$

Teraz możemy wyrazić,

$$\frac{a}{R_\ast} = \frac{2P}{\pi} D^{\frac{1}{4}}(t^2_T - t^2_F)^{-\frac{1}{2}}$$

Dla gwiazd sekwencji głównej,

$$R_\ast \propto M^\alpha_\ast$$

$$\frac{R_\ast}{R_0} \propto \left ( \frac{M_\ast}{M_0}\right )^\alpha$$

To daje R∗.

W związku z tym otrzymujemy również wartość „a”.

Otrzymujemy więc „R _p ”, „ap”, a nawet „i”.

Za to wszystko

$$h \leq R_\ast + R_p$$

$$a\: cos\: i \leq R_\ast + R_p$$

Nawet ~ 89 stopni czas tranzytu jest bardzo krótki. Planeta musi być bardzo blisko, aby uzyskać wystarczający czas tranzytu. Daje to ścisłe ograniczenie „i”. Gdy otrzymamy „i”, możemy wyprowadzić „m _p ” z pomiaru prędkości radialnej.

To wykrycie metodą tranzytu nazywa się wykrywaniem przypadkowym, tj. Prawdopodobieństwem zaobserwowania tranzytu. Obliczenia prawdopodobieństwa przejazdu (prawdopodobieństwa obserwacji) przedstawiono poniżej.

Prawdopodobieństwo przejścia jest związane z kątem bryłowym wyznaczonym przez dwie skrajne konfiguracje tranzytu, który jest -

$$Solid \: angle \:of \:planet \: = 2\pi \left ( \frac{2R_\ast}{a} \right )$$

Jak również całkowity kąt bryłowy na półosi wielkiej a, lub -

$$Solid \:angle \:of \:sphere \: =\: 4\pi$$

Prawdopodobieństwo to stosunek tych dwóch obszarów -

$$= \: \frac{area \:of\: sky \: covered \:by\: favourable \: orientation}{area\: of\: sky \:covered\: by\: all\: possible\: orientation\: of\: orbit}$$

$= \frac{4\pi a_pR_\ast}{4\pi a^2_p} = \frac{R_\ast}{a_p}$ $\frac{area\: of\: hollow \: cyclinder}{area\: of\: sphere}$

To prawdopodobieństwo jest niezależne od obserwatora.

Punkty do zapamiętania

• Aby ustalić rozmiar, zastosowano metodę tranzytu (Kosmiczny Teleskop Keplera).
• Wykrywanie metodą tranzytu to wykrycie przypadkowe.
• Planeta musi być bardzo blisko, aby uzyskać wystarczający czas tranzytu.
• Prawdopodobieństwo tranzytu jest związane z kątem bryłowym planety.
• Prawdopodobieństwo to jest niezależne od układu odniesienia obserwatora.

Pierwszy bezpośredni obraz planety pozasłonecznej w 2004 roku przedstawiał planetę o masie 3-10 M_jupiter krążący wokół brązowego karła (2M1207) o masie 25 M_jupiter. Do wykrywania egzoplanet zastosowano techniki takie jak prędkość radialna, tranzyt, mikrosoczewkowanie grawitacyjne, obrazowanie, astrometria itp. Liczba wykryć rośnie z każdym rokiem.

Do około 2010 roku metoda prędkości radialnych była szeroko stosowana, ale obecnie większość detekcji jest wykonywana metodą Transit. Nastąpił gwałtowny wzrost liczby wykryć w 2014 r., A wtedyKepler Space Telescope (KST) zaczął przynosić rezultaty.

Rozkład mas w okresie pokazuje, że metoda prędkości radialnej jest bardziej ukierunkowana na wykrywanie masywnych planet o dłuższym okresie, podczas gdy przy użyciu metody tranzytu planety o niższym okresie są wykrywane tylko tak, jak pokazano na poniższym obrazku (dzięki uprzejmości: Archiwum egzoplanet NASA) .

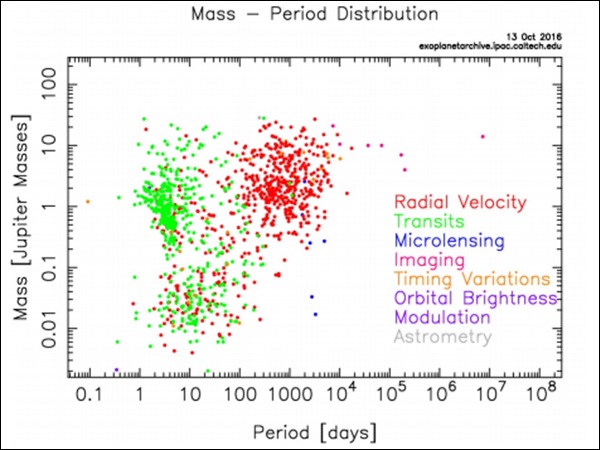
Od czasu pojawienia się KST nastąpił kolosalny wzrost liczby wykrywanych planet o mniejszej masie. Widać to na poniższym rysunku. Planety wykryte przez KST są podzielone na dwie grupy: gorące planety masywne zwane „gorącymi jowiszami” i planety o niższej masie zwane „gorącymi superziemiami” (ponieważ są masywniejsze od Ziemi).

Kiedy wykreślamy liczbę wykrytych planet pozasłonecznych w funkcji odległości do nich, okazuje się, że większość z tych planet znajduje się w odległości do 2 kpc, czyli w granicach naszej galaktyki. Być może planety nie są tak rzadkie we wszechświecie, ponieważ nasze wykrywanie ogranicza się tylko do określonego typu planet w bardzo małej części wszechświata.

Planety powstają z circumstellar disc lub proto planetary disc. Jeśli planety powstają jako produkt uboczny podczas formowania się gwiazd, być może liczba planet we wszechświecie przekracza liczbę gwiazd we wszechświecie !!

Strefy mieszkalne

Strefę nadającą się do zamieszkania można zdefiniować jako strefę wokół gwiazdy, w której może istnieć woda w postaci ciekłej. Rozważmy planetę w oddali$a_p$od gwiazdy, jak pokazano na poniższym rysunku. Poniżej opisano prostą metodę obliczania temperatury planety.

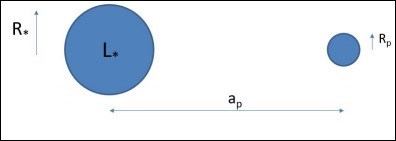
$$\left ( \frac{L_\ast}{4\pi a^2_p} \right )\pi R^2_p(1 - A) = 4\pi R^2_p \sigma T^4_p$$

i

$$\frac{L_\ast}{4\pi R^2_\ast} = \sigma T^4_\ast$$

$$\therefore T_p = (1 - A)T_\ast \sqrt{\frac{R_\ast}{2a_p}}$$

W naszym przypadku podstawianie

• L_sun = 3.83 x 10²⁶

• a_p = 1.5 ∗ 10¹¹ and

• A = 0.3

Da $T_{Earth} = 255K$. Rzeczywiste obliczenia są bardzo złożone, w tym fizyka chmur. Strefa nadająca się do zamieszkania w naszym Układzie Słonecznym leży między 0,9 a 1,7 jednostki astronomicznej.

Stwierdzono, że jasność Słońca wzrasta z czasem z powodu malejącego ciśnienia gazu. Kiedy zaczął spalać wodór, było o 30% mniej jasne. Skutkowałoby to przesunięciem ekosfery z dala od Słońca. Ponieważ Ziemia znajduje się blisko wewnętrznej krawędzi strefy zamieszkałej, być może pewnego dnia wyjdzie ze strefy!

Strefa stale nadająca się do zamieszkania

W skrócie jest określany jako CHZmożna zdefiniować jako region, w którym woda w stanie ciekłym może istnieć przez cały czas życia gwiazdy w ciągu głównym. KST wykrył wiele planet pozasłonecznych, które leżą w ekosferze.

Podpis biologiczny to każda substancja - na przykład pierwiastek, izotop, cząsteczka lub zjawisko, które dostarcza naukowych dowodów na przeszłe lub obecne życie. Przykładem jest wykrywanie zarówno O _{2, jak} i CO ₂ na planecie, co zwykle nie jest możliwe tylko w wyniku procesów geologicznych. To wykrywanie odbywa się poprzez analizę widm absorpcji.

Punkty do zapamiętania

• Do wykrywania egzoplanet zastosowano techniki takie jak prędkość radialna, tranzyt, mikrosoczewkowanie grawitacyjne, obrazowanie, astrometria itp.

• Metoda prędkości radialnych jest bardziej ukierunkowana na wykrywanie masywnych planet o dłuższym okresie.

• Gorące, masywne planety nazywane są „gorącym Jowiszem”, a planety o niższej masie nazywane są „gorącymi super ziemiami”.

• Liczba planet we wszechświecie przewyższa liczbę gwiazd we wszechświecie.

• Strefę nadającą się do zamieszkania można zdefiniować jako strefę wokół gwiazdy, w której może istnieć woda w postaci ciekłej.