DSP - Classificação de sinais DT
Assim como os sinais de tempo contínuo, os sinais de tempo discreto podem ser classificados de acordo com as condições ou operações nos sinais.
Sinais pares e ímpares
Even Signal
Um sinal é considerado par ou simétrico se satisfizer a seguinte condição;
$$ x (-n) = x (n) $$
Aqui, podemos ver que x (-1) = x (1), x (-2) = x (2) e x (-n) = x (n). Portanto, é um sinal uniforme.
Sinal ímpar
Um sinal é considerado ímpar se satisfizer a seguinte condição;
$$ x (-n) = -x (n) $$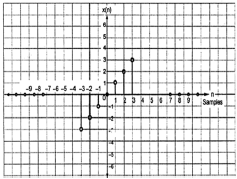
Na figura, podemos ver que x (1) = -x (-1), x (2) = -x (2) e x (n) = -x (-n). Portanto, é um sinal estranho e também anti-simétrico.
Sinais Periódicos e Não Periódicos
Um sinal de tempo discreto é periódico se, e somente se, satisfaz a seguinte condição -
$$ x (n + N) = x (n) $$Aqui, o sinal x (n) se repete após N período. Isso pode ser melhor compreendido considerando um sinal de cosseno -
$$ x (n) = A \ cos (2 \ pi f_ {0} n + \ theta) $$ $$ x (n + N) = A \ cos (2 \ pi f_ {0} (n + N) + \ theta) = A \ cos (2 \ pi f_ {0} n + 2 \ pi f_ {0} N + \ theta) $$ $$ = A \ cos (2 \ pi f_ {0} n + 2 \ pi f_ {0} N + \ theta) $$Para que o sinal se torne periódico, as seguintes condições devem ser satisfeitas;
$$ x (n + N) = x (n) $$ $$ \ Rightarrow A \ cos (2 \ pi f_ {0} n + 2 \ pi f_ {0} N + \ theta) = A \ cos (2 \ pi f_ {0} n + \ theta) $$ou seja, $ 2 \ pi f_ {0} N $ é um múltiplo integral de $ 2 \ pi $
$$ 2 \ pi f_ {0} N = 2 \ pi K $$ $$ \ Rightarrow N = \ frac {K} {f_ {0}} $$As frequências de sinais sinusoidais discretos são separadas por múltiplos inteiros de $ 2 \ pi $.
Energia e sinais de potência
Sinal de Energia
A energia de um sinal de tempo discreto é denotada como E. Matematicamente, pode ser escrita como;
$$ E = \ displaystyle \ sum \ limits_ {n = - \ infty} ^ {+ \ infty} | x (n) | ^ 2 $$Se cada valor individual de $ x (n) $ for elevado ao quadrado e adicionado, obteremos o sinal de energia. Aqui $ x (n) $ é o sinal de energia e sua energia é finita ao longo do tempo, ou seja, $ 0 <E <\ infty $
Sinal de energia
A potência média de um sinal discreto é representada como P. Matematicamente, isso pode ser escrito como;
$$ P = \ lim_ {N \ to \ infty} \ frac {1} {2N + 1} \ displaystyle \ sum \ limits_ {n = -N} ^ {+ N} | x (n) | ^ 2 $$Aqui, a potência é finita, ou seja, 0 <P <∞. No entanto, existem alguns sinais que não pertencem nem ao sinal de energia nem ao tipo de energia.