DSP - Sistemas Invariantes no Tempo
Para um sistema invariante no tempo, a saída e a entrada devem ser atrasadas por alguma unidade de tempo. Qualquer atraso fornecido na entrada deve ser refletido na saída para um sistema invariante no tempo.
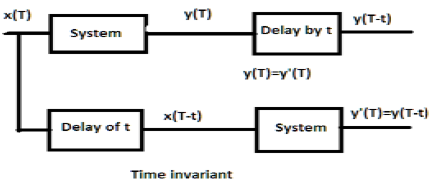
Exemplos
a) $y(T) = x(2T)$
Se for a expressão acima, ela é primeiro passada pelo sistema e depois pelo retardo (conforme mostrado na parte superior da figura); então a saída se tornará $ x (2T-2t) $. Agora, a mesma expressão é passada primeiro por um intervalo de tempo e depois pelo sistema (conforme mostrado na parte inferior da figura). A saída se tornará $ x (2T-t) $.
Portanto, o sistema não é invariante no tempo.
b) $y(T) = \sin [x(T)]$
Se o sinal for passado primeiro pelo sistema e depois pelo processo de retardo, a saída será $ \ sin x (Tt) $. Da mesma forma, se o sistema passar primeiro pelo retardo de tempo e depois pelo sistema, a saída será $ \ sin x (Tt) $. Podemos ver claramente que ambas as saídas são as mesmas. Portanto, o sistema é invariante no tempo.