DSP - Transformada Rápida de Fourier
Nos métodos DFT anteriores, vimos que a parte computacional é muito longa. Queremos reduzir isso. Isso pode ser feito por meio de FFT ou transformada rápida de Fourier. Assim, podemos dizer que FFT nada mais é do que cálculo da transformada discreta de Fourier em um formato algorítmico, onde a parte computacional será reduzida.
A principal vantagem de ter FFT é que através dela podemos projetar os filtros FIR. Matematicamente, o FFT pode ser escrito da seguinte maneira;
$$ x [K] = \ displaystyle \ sum \ limits_ {n = 0} ^ {N-1} x [n] W_N ^ {nk} $$Vamos dar um exemplo para entendê-lo melhor. Consideramos oito pontos nomeados de $ x_0 \ quad a \ quad x_7 $. Escolheremos os termos pares em um grupo e os termos ímpares no outro. A visão esquemática do dito acima foi mostrada abaixo -
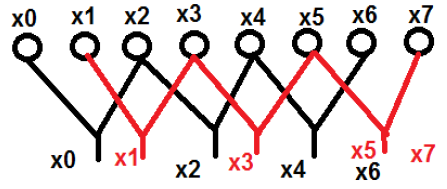
Aqui, os pontos x 0 , x 2 , x 4 ex 6 foram agrupados em uma categoria e, da mesma forma, os pontos x 1 , x 3 , x 5 ex 7 foram colocados em outra categoria. Agora, podemos torná-los ainda mais em um grupo de dois e prosseguir com o cálculo. Agora, vamos ver como a divisão em mais dois está ajudando na computação.
$ x [k] = \ displaystyle \ sum \ limits_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_N ^ {2rk} + \ displaystyle \ sum \ limits_ {r = 0 } ^ {\ frac {N} {2} -1} x [2r + 1] W_N ^ {(2r + 1) k} $
$ = \ sum_ {r = 0} ^ {\ frac {N} {2} -1} x [2r] W_ {N / 2} ^ {rk} + \ sum_ {r = 0} ^ {\ frac {N } {2} -1} x [2r + 1] W_ {N / 2} ^ {rk} \ vezes W_N ^ k $
$ = G [k] + H [k] \ vezes W_N ^ k $
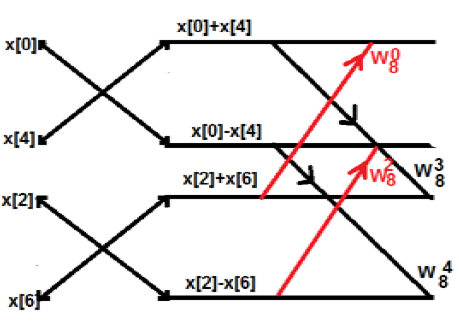
Inicialmente, pegamos uma sequência de oito pontos, mas depois dividimos aquela em duas partes G [k] e H [k]. G [k] representa a parte par, enquanto H [k] representa a parte ímpar. Se quisermos realizá-lo por meio de um diagrama, ele pode ser mostrado como abaixo -
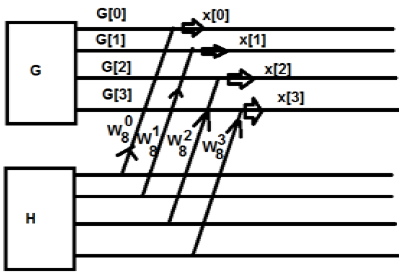
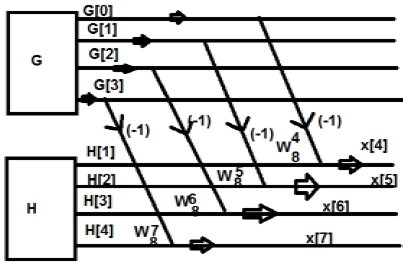
Na figura acima, podemos ver que
$ W_8 ^ 4 = -1 $
$ W_8 ^ 5 = -W_8 ^ 1 $
$ W_8 ^ 6 = -W_8 ^ 2 $
$ W_8 ^ 7 = -W_8 ^ 3 $
Da mesma forma, os valores finais podem ser escritos da seguinte forma -
$ G [0] -H [0] = x [4] $
$ G [1] -W_8 ^ 1H [1] = x [5] $
$ G [2] -W_8 ^ 2H [2] = x [6] $
$ G [1] -W_8 ^ 3H [3] = x [7] $
O acima é uma série periódica. A desvantagem deste sistema é que K não pode ser quebrado além de 4 pontos. Agora vamos dividir o acima em mais. Vamos obter as estruturas mais ou menos assim
Exemplo
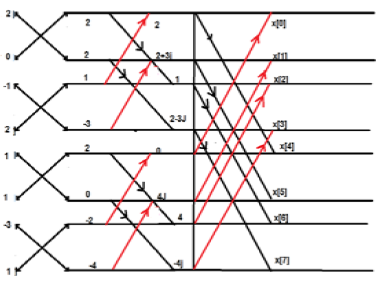
Considere a sequência x [n] = {2,1, -1, -3,0,1,2,1}. Calcule o FFT.
Solution - A sequência fornecida é x [n] = {2,1, -1, -3,0,1,2,1}
Organize os termos conforme mostrado abaixo;