DSP - Sinais Diversos
Existem outros sinais, que são resultado da operação executada neles. Alguns tipos comuns de sinais são discutidos abaixo.
Sinais Conjugados
Os sinais que satisfazem a condição $ x (t) = x * (- t) $ são chamados de sinais conjugados.
Seja $ x (t) = a (t) + jb (t) $ ... eqn. 1
Então, $ x (-t) = a (-t) + jb (-t) $
E $ x * (- t) = a (-t) -jb (-t) $ ... eqn. 2
Por condição, $ x (t) = x * (- t) $
Se compararmos as equações derivadas 1 e 2, podemos ver que a parte real é par, enquanto a parte imaginária é ímpar. Esta é a condição para um sinal ser do tipo conjugado.
Sinais antissimétricos conjugados
Os sinais que satisfazem a condição $ x (t) = -x * (- t) $ são chamados de sinais antissimétricos conjugados
Seja $ x (t) = a (t) + jb (t) $ ... eqn. 1
Então $ x (-t) = a (-t) + jb (-t) $
E $ x * (- t) = a (-t) -jb (-t) $
$ -x * (- t) = -a (-t) + jb (-t) $ ... eqn. 2
Por condição $ x (t) = -x * (- t) $
Agora, novamente compare as duas equações da mesma forma que fizemos para os sinais conjugados. Aqui, descobriremos que a parte real é ímpar e a parte imaginária é par. Esta é a condição para que um sinal se torne do tipo antissimétrico conjugado.
Exemplo
Seja o sinal dado $ x (t) = \ sin t + jt ^ {2} $.
Aqui, a parte real sendo $ \ sin t $ é ímpar e a parte imaginária sendo $ t ^ 2 $ é par. Portanto, este sinal pode ser classificado como sinal antissimétrico conjugado.
Qualquer função pode ser dividida em duas partes. Uma parte sendo simetria do conjugado e a outra parte sendo antissimétrica conjugada. Portanto, qualquer sinal x (t) pode ser escrito como
$$ x (t) = xcs (t) + xcas (t) $$Onde $ xcs (t) $ é o sinal simétrico conjugado e $ xcas (t) $ é o sinal anti-simétrico conjugado
$$ xcs (t) = \ frac {[x (t) + x * (- t)]} {2} $$E
$$ xcas (t) = \ frac {[x (t) -x * (- t)]} {2} $$Sinais simétricos de meia onda
Quando um sinal satisfaz a condição $ cx (t) = -x (t \ pm (\ frac {T_ {0}} {2})) $, é chamado de sinal simétrico de meia onda. Aqui, a inversão de amplitude e a mudança de tempo do sinal ocorrem pela metade. Para sinal simétrico de meia onda, o valor médio será zero, mas este não é o caso quando a situação é inversa.
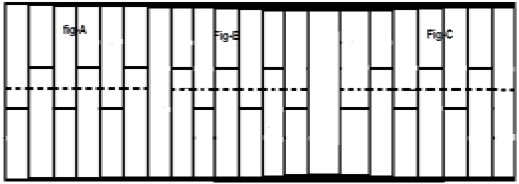
Considere um sinal x (t) conforme mostrado na figura A acima. O primeiro passo é deslocar o sinal no tempo e torná-lo $ x [t - (\ frac {T} {2})] $. Assim, o novo sinal é alterado conforme mostrado na figura B. Em seguida, invertemos a amplitude do sinal, ou seja, tornamos $ -x [t - (\ frac {T} {2})] $ como mostrado na figura C. Visto que este sinal se repete após a mudança de meio tempo e inversão de amplitude, é um sinal simétrico de meia onda.
Sinal Ortogonal
Dois sinais x (t) ey (t) são ditos ortogonais se satisfizerem as duas condições a seguir.
Condition 1 - $ \ int _ {- \ infty} ^ {\ infty} x (t) y (t) = 0 $ [para sinal não periódico]
Condition 2 - $ \ int x (t) y (t) = 0 $ [Para sinal periódico]
Os sinais, que contêm harmônicos ímpares ( 3º , 5º , 7º ... etc.) E têm frequências diferentes, são mutuamente ortogonais entre si.
Em sinais de tipo trigonométrico, as funções seno e cosseno também são ortogonais entre si; desde que tenham a mesma frequência e estejam na mesma fase. Da mesma maneira, os sinais DC (sinais de corrente contínua) e senoidais também são ortogonais entre si. Se x (t) ey (t) são dois sinais ortogonais e $ z (t) = x (t) + y (t) $ então a potência e a energia de z (t) podem ser escritas como;
$$ P (z) = p (x) + p (y) $$ $$ E (z) = E (x) + E (y) $$Exemplo
Analise o sinal: $ z (t) = 3 + 4 \ sin (2 \ pi t + 30 ^ 0) $
Aqui, o sinal é composto por um sinal DC (3) e uma função seno. Portanto, por propriedade, este sinal é um sinal ortogonal e os dois sub-sinais nele são mutuamente ortogonais entre si.