DSP - Integração de Operações em Sinais
Integração de qualquer sinal significa a soma desse sinal em domínio de tempo particular para obter um sinal modificado. Matematicamente, isso pode ser representado como -
$$ x (t) \ rightarrow y (t) = \ int _ {- \ infty} ^ {t} x (t) dt $$Aqui também, na maioria dos casos, podemos fazer integração matemática e encontrar o sinal resultante, mas a integração direta em rápida sucessão é possível para sinais que são representados graficamente em formato retangular. Assim como a diferenciação, aqui também iremos consultar uma tabela para obter o resultado rapidamente.
| Sinal Original | Sinal Integrado |
|---|---|
| 1 | impulso |
| Impulso | degrau |
| Degrau | Rampa |
Exemplo
Vamos considerar um sinal $ x (t) = u (t) -u (t-3) $. É mostrado na Fig-1 abaixo. Claramente, podemos ver que é um sinal de degrau. Agora vamos integrá-lo. Referindo-se à tabela, sabemos que a integração do sinal de degrau produz um sinal de rampa.
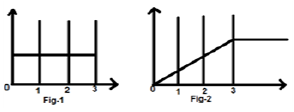
No entanto, vamos calculá-lo matematicamente,
$ y (t) = \ int _ {- \ infty} ^ {t} x (t) dt $
$ = \ int _ {- \ infty} ^ {t} [u (t) -u (t-3)] dt $
$ = \ int _ {- \ infty} ^ {t} u (t) dt- \ int _ {- \ infty} ^ {t} u (t-3) dt $
$ = r (t) -r (t-3) $
O mesmo é plotado como mostrado na fig-2,