ระบบควบคุม - บล็อกไดอะแกรม
บล็อกไดอะแกรมประกอบด้วยบล็อกเดียวหรือบล็อกรวมกัน สิ่งเหล่านี้ใช้เพื่อแสดงระบบควบคุมในรูปแบบภาพ
องค์ประกอบพื้นฐานของแผนภาพบล็อก
องค์ประกอบพื้นฐานของแผนภาพบล็อกคือบล็อกจุดรวมและจุดขึ้นเครื่องบิน ให้เราพิจารณาแผนภาพบล็อกของระบบควบคุมวงปิดดังแสดงในรูปต่อไปนี้เพื่อระบุองค์ประกอบเหล่านี้

แผนภาพบล็อกด้านบนประกอบด้วยสองบล็อกที่มีฟังก์ชันการถ่ายโอน G (s) และ H (s) นอกจากนี้ยังมีจุดสรุปหนึ่งจุดและจุดขึ้นเครื่องหนึ่งจุด ลูกศรระบุทิศทางการไหลของสัญญาณ ตอนนี้ให้เราพูดถึงองค์ประกอบเหล่านี้ทีละรายการ
บล็อก
ฟังก์ชันการถ่ายโอนของส่วนประกอบจะแสดงโดยบล็อก บล็อกมีอินพุตเดียวและเอาต์พุตเดียว
รูปต่อไปนี้แสดงบล็อกที่มีอินพุต X, เอาต์พุต Y (s) และฟังก์ชันการถ่ายโอน G (s)

Transfer Function, $ G (s) = \ frac {Y (s)} {X (s)} $
$$ \ Rightarrow Y (s) = G (s) X (s) $$
ผลลัพธ์ของบล็อกได้มาจากการคูณฟังก์ชันการถ่ายโอนของบล็อกด้วยอินพุต
จุดสรุป
จุดรวมจะแสดงด้วยวงกลมที่มีกากบาท (X) อยู่ข้างใน มีสองอินพุตหรือมากกว่าและเอาต์พุตเดี่ยว สร้างผลรวมพีชคณิตของปัจจัยการผลิต นอกจากนี้ยังทำการรวมหรือการลบหรือการรวมกันของการรวมและการลบของอินพุตตามขั้วของอินพุต ให้เราดูการดำเนินการทั้งสามนี้ทีละรายการ
รูปต่อไปนี้แสดงจุดรวมที่มีสองอินพุต (A, B) และหนึ่งเอาต์พุต (Y) ที่นี่อินพุต A และ B มีเครื่องหมายบวก ดังนั้นจุดสรุปจะสร้างผลลัพธ์ Y assum of A and B.
กล่าวคือ Y = A + B

รูปต่อไปนี้แสดงจุดรวมที่มีสองอินพุต (A, B) และหนึ่งเอาต์พุต (Y) ที่นี่อินพุต A และ B มีสัญญาณตรงข้ามกันคือ A มีเครื่องหมายบวกและ B มีเครื่องหมายลบ ดังนั้นจุดรวมจึงสร้างผลลัพธ์Y เป็น difference of A and B.
Y = A + (-B) = A - B

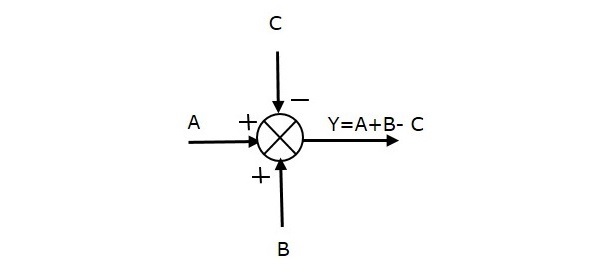
รูปต่อไปนี้แสดงจุดรวมที่มีอินพุตสามตัว (A, B, C) และหนึ่งเอาต์พุต (Y) ที่นี่อินพุต A และ B มีสัญญาณบวกและ C มีเครื่องหมายลบ ดังนั้นจุดรวมจึงสร้างผลลัพธ์Y เช่น
Y = A + B + (−C) = A + B - ค.
จุดขึ้นเครื่องบิน
จุดขึ้น - ลงคือจุดที่สัญญาณอินพุตเดียวกันสามารถส่งผ่านได้มากกว่าหนึ่งสาขา นั่นหมายความว่าด้วยความช่วยเหลือของจุดเริ่มต้นเราสามารถใช้อินพุตเดียวกันกับหนึ่งบล็อกหรือมากกว่าโดยรวมคะแนนได้
ในรูปต่อไปนี้จุดเริ่มต้นใช้เพื่อเชื่อมต่ออินพุตเดียวกัน R กับอีกสองบล็อก

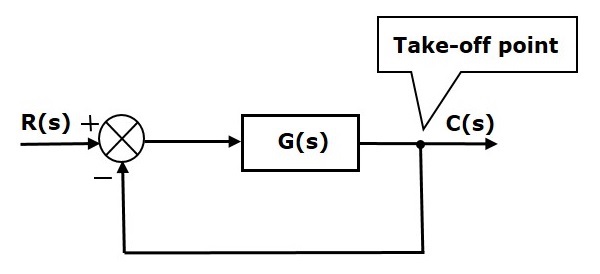
ในรูปต่อไปนี้จุดขึ้น - ลงใช้เพื่อเชื่อมต่อเอาท์พุท C (s) เป็นหนึ่งในอินพุตไปยังจุดรวม
การแสดงแผนภาพบล็อกของระบบไฟฟ้า
ในส่วนนี้ให้เราแสดงระบบไฟฟ้าด้วยแผนภาพบล็อก ระบบไฟฟ้าประกอบด้วยองค์ประกอบพื้นฐานสามประการ -resistor, inductor and capacitor.
พิจารณาชุดวงจร RLC ดังแสดงในรูปต่อไปนี้ โดยที่ V i (t) และ V o (t) คือแรงดันไฟฟ้าขาเข้าและขาออก ให้ i (t) เป็นกระแสที่ไหลผ่านวงจร วงจรนี้อยู่ในโดเมนเวลา

เมื่อใช้การแปลงลาปลาซกับวงจรนี้จะได้วงจรใน s-domain วงจรดังแสดงในรูปต่อไปนี้
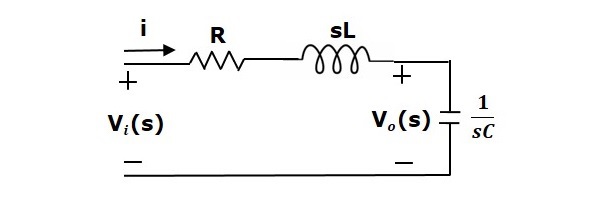
จากวงจรข้างต้นเราสามารถเขียนได้
$$ ฉัน (s) = \ frac {V_i (s) -V_o (s)} {R + sL} $$
$ \ Rightarrow I (s) = \ left \ {\ frac {1} {R + sL} \ right \} \ left \ {V_i (s) -V_o (s) \ right \} $ (Equation 1)
$ V_o (s) = \ left (\ frac {1} {sC} \ right) I (s) $ (Equation 2)
ตอนนี้ให้เราวาดแผนภาพบล็อกสำหรับสองสมการนี้ทีละสมการ จากนั้นรวมบล็อกไดอะแกรมเหล่านั้นให้ถูกต้องเพื่อให้ได้บล็อกไดอะแกรมโดยรวมของซีรีส์ RLC Circuit (s-domain)
สมการ 1 สามารถนำไปใช้กับบล็อกที่มีฟังก์ชันการถ่ายโอน $ \ frac {1} {R + sL} $ อินพุตและเอาต์พุตของบล็อกนี้คือ $ \ left \ {V_i (s) -V_o (s) \ right \} $ และ $ I (s) $ เราต้องการจุดรวมเพื่อรับ $ \ left \ {V_i (s) -V_o (s) \ right \} $ แผนภาพบล็อกของสมการ 1 แสดงดังรูปต่อไปนี้

สมการ 2 สามารถนำไปใช้กับบล็อกที่มีฟังก์ชันการถ่ายโอน $ \ frac {1} {sC} $ อินพุตและเอาต์พุตของบล็อกนี้คือ $ I (s) $ และ $ V_o (s) $ แผนภาพบล็อกของสมการ 2 แสดงดังรูปต่อไปนี้

แผนภาพบล็อกโดยรวมของชุดของวงจร RLC (s-domain) แสดงดังรูปต่อไปนี้

ในทำนองเดียวกันคุณสามารถวาดไฟล์ block diagram ของวงจรไฟฟ้าหรือระบบใด ๆ เพียงทำตามขั้นตอนง่ายๆนี้
แปลงวงจรไฟฟ้าโดเมนเวลาเป็นวงจรไฟฟ้า s-domain โดยใช้การแปลงลาปลาซ
เขียนสมการสำหรับกระแสที่ไหลผ่านองค์ประกอบสาขาอนุกรมและแรงดันไฟฟ้าในกิ่งปัดทั้งหมด
วาดแผนภาพบล็อกสำหรับสมการข้างต้นทั้งหมดทีละรายการ
รวมบล็อกไดอะแกรมทั้งหมดเหล่านี้อย่างเหมาะสมเพื่อให้ได้บล็อกไดอะแกรมโดยรวมของวงจรไฟฟ้า (s-domain)