การสร้างแบบจำลองของระบบเครื่องกล
ในบทนี้ให้เราพูดถึงไฟล์ differential equation modelingของระบบเครื่องกล ระบบกลไกตามประเภทของการเคลื่อนที่มีสองประเภท
- ระบบกลไกแปล
- ระบบกลไกหมุน
การสร้างแบบจำลองของระบบเครื่องกลแปล
ระบบกลไกแปลเคลื่อนไปตามก straight line. ระบบเหล่านี้ส่วนใหญ่ประกอบด้วยองค์ประกอบพื้นฐานสามประการ สิ่งเหล่านี้คือมวลสปริงและแดชพอตหรือแดมเปอร์
ถ้าแรงถูกนำไปใช้กับระบบกลไกการแปลจะถูกต่อต้านโดยกองกำลังของฝ่ายตรงข้ามเนื่องจากมวลความยืดหยุ่นและแรงเสียดทานของระบบ เนื่องจากแรงที่กระทำและแรงตรงข้ามอยู่ในทิศทางตรงกันข้ามผลรวมพีชคณิตของแรงที่กระทำต่อระบบจึงเป็นศูนย์ ตอนนี้ให้เราดูแรงที่ต่อต้านโดยองค์ประกอบทั้งสามนี้ทีละรายการ
มวล
มวลเป็นทรัพย์สินของร่างกายซึ่งจัดเก็บ kinetic energy. หากมีการใช้แรงกับร่างกายที่มีมวลMจากนั้นจะถูกต่อต้านโดยกองกำลังฝ่ายตรงข้ามเนื่องจากมวล แรงต่อต้านนี้เป็นสัดส่วนกับความเร่งของร่างกาย สมมติว่าความยืดหยุ่นและแรงเสียดทานมีค่าเล็กน้อย

$$ F_m \ propto \: a $$
$$ \ Rightarrow F_m = Ma = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} $$
$$ F = F_m = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} $$
ที่ไหน
F คือแรงที่ใช้
Fm คือแรงต่อต้านเนื่องจากมวล
M คือมวล
a คือการเร่งความเร็ว
x คือการกระจัด
ฤดูใบไม้ผลิ
ฤดูใบไม้ผลิเป็นองค์ประกอบที่เก็บ potential energy. หากมีการใช้แรงกับสปริงKจากนั้นจะถูกต่อต้านโดยแรงต่อต้านเนื่องจากความยืดหยุ่นของสปริง แรงตรงข้ามนี้เป็นสัดส่วนกับการกระจัดของสปริง สมมติว่ามวลและแรงเสียดทานมีค่าเล็กน้อย

$$ F \ propto \: x $$
$$ \ Rightarrow F_k = Kx $$
$$ F = F_k = Kx $$
ที่ไหน
F คือแรงที่ใช้
Fk เป็นแรงต่อต้านเนื่องจากความยืดหยุ่นของสปริง
K คือค่าคงที่ของสปริง
x คือการกระจัด
Dashpot
หากมีการบังคับใช้กับ dashpot Bจากนั้นจะถูกต่อต้านโดยกองกำลังฝ่ายตรงข้ามเนื่องจาก frictionของ dashpot แรงตรงข้ามนี้เป็นสัดส่วนกับความเร็วของร่างกาย สมมติว่ามวลและความยืดหยุ่นมีค่าเล็กน้อย

$$ F_b \ propto \: \ nu $$
$$ \ Rightarrow F_b = B \ nu = B \ frac {\ text {d} x} {\ text {d} t} $$
$$ F = F_b = B \ frac {\ text {d} x} {\ text {d} t} $$
ที่ไหน
Fb คือแรงต่อต้านเนื่องจากการเสียดสีของแดชพอต
B คือค่าสัมประสิทธิ์แรงเสียดทาน
v คือความเร็ว
x คือการกระจัด
การสร้างแบบจำลองของระบบเครื่องกลหมุน
ระบบกลไกหมุนเคลื่อนที่ไปเกี่ยวกับแกนคงที่ ระบบเหล่านี้ส่วนใหญ่ประกอบด้วยองค์ประกอบพื้นฐานสามประการ นั่นคือmoment of inertia, torsional spring และ dashpot.
ถ้าแรงบิดถูกนำไปใช้กับระบบกลไกแบบหมุนมันจะถูกต่อต้านโดยแรงบิดของฝ่ายตรงข้ามเนื่องจากโมเมนต์ความเฉื่อยความยืดหยุ่นและแรงเสียดทานของระบบ เนื่องจากแรงบิดที่ใช้และแรงบิดของฝ่ายตรงข้ามอยู่ในทิศทางตรงกันข้ามผลรวมของแรงบิดพีชคณิตที่กระทำต่อระบบจึงเป็นศูนย์ ตอนนี้ให้เราดูแรงบิดที่ตรงข้ามกับองค์ประกอบทั้งสามนี้ทีละรายการ
ช่วงเวลาแห่งความเฉื่อย
ในระบบกลไกแปลมวลจะเก็บพลังงานจลน์ ในทำนองเดียวกันในระบบกลไกการหมุนช่วงเวลาของร้านค้าความเฉื่อยkinetic energy.
หากมีการใช้แรงบิดกับร่างกายที่มีโมเมนต์ความเฉื่อย Jจากนั้นจะถูกต่อต้านโดยแรงบิดตรงข้ามเนื่องจากช่วงเวลาแห่งความเฉื่อย แรงบิดตรงข้ามนี้เป็นสัดส่วนกับความเร่งเชิงมุมของร่างกาย สมมติว่าความยืดหยุ่นและแรงเสียดทานมีค่าเล็กน้อย

$$ T_j \ propto \: \ alpha $$
$$ \ Rightarrow T_j = J \ alpha = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} $$
$$ T = T_j = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} $$
ที่ไหน
T คือแรงบิดที่ใช้
Tj คือแรงบิดตรงข้ามเนื่องจากโมเมนต์ความเฉื่อย
J เป็นช่วงเวลาแห่งความเฉื่อย
α คือความเร่งเชิงมุม
θ คือการกระจัดเชิงมุม
สปริงแรงบิด
ในระบบกลไกแปลสปริงจะเก็บพลังงานศักย์ ในทำนองเดียวกันในระบบกลไกแบบหมุนร้านสปริงแบบบิดpotential energy.
หากมีการใช้แรงบิดกับสปริงบิด Kจากนั้นจะถูกต่อต้านโดยแรงบิดตรงข้ามเนื่องจากความยืดหยุ่นของสปริงบิด แรงบิดที่ตรงกันข้ามนี้เป็นสัดส่วนกับการกระจัดเชิงมุมของสปริงบิด สมมติว่าโมเมนต์ความเฉื่อยและแรงเสียดทานมีค่าเล็กน้อย
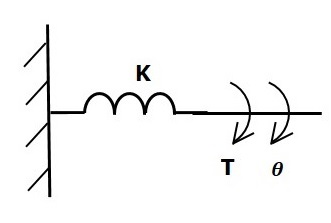
$$ T_k \ propto \: \ theta $$
$$ \ Rightarrow T_k = K \ theta $$
$$ T = T_k = K \ theta $$
ที่ไหน
T คือแรงบิดที่ใช้
Tk คือแรงบิดที่ตรงกันข้ามเนื่องจากความยืดหยุ่นของสปริงบิด
K คือค่าคงที่ของสปริงบิด
θ คือการกระจัดเชิงมุม
Dashpot
หากมีการใช้แรงบิดบนแดชพอต Bจากนั้นจะถูกต่อต้านโดยแรงบิดตรงข้ามเนื่องจาก rotational frictionของ dashpot แรงบิดตรงข้ามนี้เป็นสัดส่วนกับความเร็วเชิงมุมของร่างกาย สมมติว่าช่วงเวลาแห่งความเฉื่อยและความยืดหยุ่นมีค่าเล็กน้อย
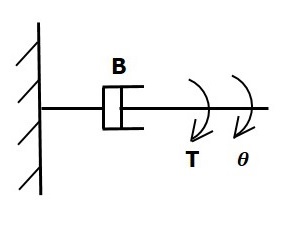
$$ T_b \ propto \: \ omega $$
$$ \ Rightarrow T_b = B \ omega = B \ frac {\ text {d} \ theta} {\ text {d} t} $$
$$ T = T_b = B \ frac {\ text {d} \ theta} {\ text {d} t} $$
ที่ไหน
Tb คือแรงบิดตรงข้ามเนื่องจากแรงเสียดทานในการหมุนของแดชพ็อต
B คือค่าสัมประสิทธิ์แรงเสียดทานของการหมุน
ω คือความเร็วเชิงมุม
θ คือการกระจัดเชิงมุม