การเปรียบเทียบทางไฟฟ้าของระบบเครื่องกล
มีการกล่าวถึงสองระบบ analogous ซึ่งกันและกันหากเป็นไปตามเงื่อนไขสองข้อต่อไปนี้
- ทั้งสองระบบมีความแตกต่างกันทางกายภาพ
- การสร้างแบบจำลองสมการเชิงอนุพันธ์ของระบบทั้งสองนี้เหมือนกัน
ระบบไฟฟ้าและระบบเครื่องกลเป็นระบบที่แตกต่างกันทางกายภาพสองระบบ การเปรียบเทียบทางไฟฟ้าของระบบกลไกแปลมีสองประเภท สิ่งเหล่านี้เป็นการเปรียบเทียบแรงดันไฟฟ้าและการเปรียบเทียบแรงในปัจจุบัน
การเปรียบเทียบแรงดันไฟฟ้า
ในการเปรียบเทียบแรงดันไฟฟ้าแรงสมการทางคณิตศาสตร์ของ translational mechanical system เปรียบเทียบกับสมการตาข่ายของระบบไฟฟ้า
พิจารณาระบบกลไกการแปลดังต่อไปนี้ดังแสดงในรูปต่อไปนี้
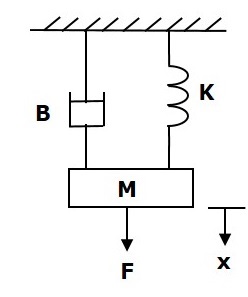
force balanced equation สำหรับระบบนี้คือ
$$ F = F_m + F_b + F_k $$
$ \ Rightarrow F = M \ frac {\ text {d} ^ 2x} {\ text {d} t ^ 2} + B \ frac {\ text {d} x} {\ text {d} t} + Kx $ (Equation 1)
พิจารณาระบบไฟฟ้าต่อไปนี้ดังแสดงในรูปต่อไปนี้ วงจรนี้ประกอบด้วยตัวต้านทานตัวเหนี่ยวนำและตัวเก็บประจุ องค์ประกอบทางไฟฟ้าทั้งหมดนี้เชื่อมต่อกันเป็นชุด แรงดันไฟฟ้าอินพุตที่ใช้กับวงจรนี้คือ $ V $ โวลต์และกระแสที่ไหลผ่านวงจรคือ $ i $ Amps

สมการตาข่ายสำหรับวงจรนี้คือ
$ V = Ri + L \ frac {\ text {d} i} {\ text {d} t} + \ frac {1} {c} \ int idt $ (Equation 2)
แทนที่ $ i = \ frac {\ text {d} q} {\ text {d} t} $ ในสมการ 2
$$ V = R \ frac {\ text {d} q} {\ text {d} t} + L \ frac {\ text {d} ^ 2q} {\ text {d} t ^ 2} + \ frac { q} {C} $$
$ \ Rightarrow V = L \ frac {\ text {d} ^ 2q} {\ text {d} t ^ 2} + R \ frac {\ text {d} q} {\ text {d} t} + \ left (\ frac {1} {c} \ right) q $ (Equation 3)
เมื่อเปรียบเทียบสมการ 1 และสมการ 3 เราจะได้ปริมาณที่คล้ายคลึงกันของระบบกลไกแปลและระบบไฟฟ้า ตารางต่อไปนี้แสดงปริมาณที่คล้ายคลึงกันเหล่านี้
| ระบบเครื่องกลแปล | ระบบไฟฟ้า |
|---|---|
| แรง (F) | แรงดันไฟฟ้า (V) |
| มวล (M) | ตัวเหนี่ยวนำ (L) |
| ค่าสัมประสิทธิ์แรงเสียดทาน (B) | ความต้านทาน (R) |
| สปริงคงที่ (K) | ซึ่งกันและกันของ Capacitance $ (\ frac {1} {c}) $ |
| การกำจัด (x) | ค่าบริการ (q) |
| ความเร็ว (v) | ปัจจุบัน (i) |
ในทำนองเดียวกันมีการเปรียบเทียบแรงบิดแรงบิดสำหรับระบบกลไกแบบหมุน ตอนนี้ให้เราพิจารณาเกี่ยวกับการเปรียบเทียบนี้
การเปรียบเทียบแรงบิดของแรงบิด
ในการเปรียบเทียบนี้สมการทางคณิตศาสตร์ของ rotational mechanical system เปรียบเทียบกับสมการตาข่ายของระบบไฟฟ้า
ระบบกลไกการหมุนแสดงในรูปต่อไปนี้

สมการสมดุลแรงบิดคือ
$$ T = T_j + T_b + T_k $$
$ \ Rightarrow T = J \ frac {\ text {d} ^ 2 \ theta} {\ text {d} t ^ 2} + B \ frac {\ text {d} \ theta} {\ text {d} t} + k \ theta $ (Equation 4)
เมื่อเปรียบเทียบสมการ 4 และสมการ 3 เราจะได้ปริมาณที่คล้ายคลึงกันของระบบกลไกการหมุนและระบบไฟฟ้า ตารางต่อไปนี้แสดงปริมาณที่คล้ายคลึงกันเหล่านี้
| ระบบเครื่องกลหมุน | ระบบไฟฟ้า |
|---|---|
| แรงบิด (T) | แรงดันไฟฟ้า (V) |
| ช่วงเวลาแห่งความเฉื่อย (J) | ตัวเหนี่ยวนำ (L) |
| ค่าสัมประสิทธิ์แรงเสียดทานในการหมุน (B) | ความต้านทาน (R) |
| สปริงแรงบิดคงที่ (K) | ซึ่งกันและกันของ Capacitance $ (\ frac {1} {c}) $ |
| การกระจัดเชิงมุม (θ) | ค่าบริการ (q) |
| ความเร็วเชิงมุม (ω) | ปัจจุบัน (i) |
บังคับให้เกิดการเปรียบเทียบในปัจจุบัน
ในการเปรียบเทียบแรงปัจจุบันสมการทางคณิตศาสตร์ของ translational mechanical system ถูกเปรียบเทียบกับสมการสำคัญของระบบไฟฟ้า
พิจารณาระบบไฟฟ้าต่อไปนี้ดังแสดงในรูปต่อไปนี้ วงจรนี้ประกอบด้วยแหล่งกระแสตัวต้านทานตัวเหนี่ยวนำและตัวเก็บประจุ องค์ประกอบทางไฟฟ้าทั้งหมดนี้เชื่อมต่อแบบขนาน

สมการที่สำคัญคือ
$ i = \ frac {V} {R} + \ frac {1} {L} \ int Vdt + C \ frac {\ text {d} V} {\ text {d} t} $ (Equation 5)
แทนที่ $ V = \ frac {\ text {d} \ Psi} {\ text {d} t} $ ในสมการ 5
$$ i = \ frac {1} {R} \ frac {\ text {d} \ Psi} {\ text {d} t} + \ left (\ frac {1} {L} \ right) \ Psi + C \ frac {\ text {d} ^ 2 \ Psi} {\ text {d} t ^ 2} $$
$ \ Rightarrow i = C \ frac {\ text {d} ^ 2 \ Psi} {\ text {d} t ^ 2} + \ left (\ frac {1} {R} \ right) \ frac {\ text { d} \ Psi} {\ text {d} t} + \ left (\ frac {1} {L} \ right) \ Psi $ (Equation 6)
เมื่อเปรียบเทียบสมการ 1 และสมการ 6 เราจะได้ปริมาณที่คล้ายคลึงกันของระบบกลไกแปลและระบบไฟฟ้า ตารางต่อไปนี้แสดงปริมาณที่คล้ายคลึงกันเหล่านี้
| ระบบเครื่องกลแปล | ระบบไฟฟ้า |
|---|---|
| แรง (F) | ปัจจุบัน (i) |
| มวล (M) | ความจุ (C) |
| ค่าสัมประสิทธิ์แรงเสียดทาน (B) | ซึ่งกันและกันของการต่อต้าน $ (\ frac {1} {R}) $ |
| ค่าคงที่ของสปริง (K) | ซึ่งกันและกันของความเหนี่ยวนำ $ (\ frac {1} {L}) $ |
| การกำจัด (x) | ฟลักซ์แม่เหล็ก (ψ) |
| ความเร็ว (v) | แรงดันไฟฟ้า (V) |
ในทำนองเดียวกันมีการเปรียบเทียบกระแสแรงบิดสำหรับระบบกลไกแบบหมุน ตอนนี้ให้เราพิจารณาการเปรียบเทียบนี้
การเปรียบเทียบแรงบิดปัจจุบัน
ในการเปรียบเทียบนี้สมการทางคณิตศาสตร์ของ rotational mechanical system ถูกเปรียบเทียบกับสมการตาข่ายปมของระบบไฟฟ้า
เมื่อเปรียบเทียบสมการ 4 และสมการ 6 เราจะได้ปริมาณที่คล้ายคลึงกันของระบบกลไกการหมุนและระบบไฟฟ้า ตารางต่อไปนี้แสดงปริมาณที่คล้ายคลึงกันเหล่านี้
| ระบบเครื่องกลหมุน | ระบบไฟฟ้า |
|---|---|
| แรงบิด (T) | ปัจจุบัน (i) |
| ช่วงเวลาแห่งความเฉื่อย (J) | ความจุ (C) |
| ค่าสัมประสิทธิ์แรงเสียดทานในการหมุน (B) | ซึ่งกันและกันของการต่อต้าน $ (\ frac {1} {R}) $ |
| สปริงแรงบิดคงที่ (K) | ซึ่งกันและกันของความเหนี่ยวนำ $ (\ frac {1} {L}) $ |
| การกระจัดเชิงมุม (θ) | ฟลักซ์แม่เหล็ก (ψ) |
| ความเร็วเชิงมุม (ω) | แรงดันไฟฟ้า (V) |
ในบทนี้เราได้กล่าวถึงการเปรียบเทียบทางไฟฟ้าของระบบกลไก การเปรียบเทียบเหล่านี้มีประโยชน์ในการศึกษาและวิเคราะห์ระบบที่ไม่ใช้ไฟฟ้าเช่นระบบเครื่องกลจากระบบไฟฟ้าแบบอะนาล็อก