ระบบควบคุม - การวิเคราะห์การตอบสนองต่อเวลา
เราสามารถวิเคราะห์การตอบสนองของระบบควบคุมทั้งในโดเมนเวลาและโดเมนความถี่ เราจะพูดถึงการวิเคราะห์การตอบสนองความถี่ของระบบควบคุมในบทต่อ ๆ ไป ตอนนี้ให้เราพูดคุยเกี่ยวกับการวิเคราะห์การตอบสนองเวลาของระบบควบคุม
เวลาตอบสนองคืออะไร?
หากเอาต์พุตของระบบควบคุมสำหรับอินพุตแตกต่างกันไปตามเวลาจะเรียกว่า time responseของระบบควบคุม การตอบสนองต่อเวลาประกอบด้วยสองส่วน
- การตอบสนองชั่วคราว
- การตอบสนองของรัฐคงที่
การตอบสนองของระบบควบคุมในโดเมนเวลาแสดงดังรูปต่อไปนี้

ที่นี่มีการระบุทั้งสถานะชั่วคราวและสถานะคงที่ในรูป การตอบสนองที่สอดคล้องกับสถานะเหล่านี้เรียกว่าการตอบสนองต่อสถานะชั่วคราวและคงที่
ในทางคณิตศาสตร์เราสามารถเขียนการตอบสนองของเวลา c (t) เป็น
$$ c (t) = c_ {tr} (t) + c_ {ss} (t) $$
ที่ไหน
- c tr (t) คือการตอบสนองชั่วคราว
- c ss (t) คือการตอบสนองของสภาวะคงที่
การตอบสนองชั่วคราว
หลังจากใช้อินพุตกับระบบควบคุมแล้วเอาต์พุตจะใช้เวลาพอสมควรในการเข้าสู่สภาวะคงที่ ดังนั้นเอาต์พุตจะอยู่ในสถานะชั่วคราวจนกว่าจะเข้าสู่สภาวะคงที่ ดังนั้นการตอบสนองของระบบควบคุมระหว่างสถานะชั่วคราวจึงเรียกว่าtransient response.
การตอบสนองชั่วคราวจะเป็นศูนย์สำหรับค่าขนาดใหญ่ของ 't' ตามหลักการแล้วค่าของ 't' นี้คืออินฟินิตี้และในทางปฏิบัติมันเป็นค่าคงที่ห้าเท่า
ในทางคณิตศาสตร์เราสามารถเขียนเป็น
$$ \ lim_ {t \ rightarrow \ infty} c_ {tr} (t) = 0 $$
การตอบสนองต่อสภาวะคงที่
ส่วนของการตอบสนองต่อเวลาที่ยังคงอยู่แม้ว่าการตอบสนองชั่วคราวจะมีค่าเป็นศูนย์สำหรับค่าขนาดใหญ่ของ 't' เรียกว่า steady state response. ซึ่งหมายความว่าการตอบสนองชั่วคราวจะเป็นศูนย์แม้ในสภาวะคงที่
Example
ให้เราค้นหาเงื่อนไขชั่วคราวและคงที่ของการตอบสนองเวลาของระบบควบคุม $ c (t) = 10 + 5e ^ {- t} $
ในที่นี้คำที่สอง $ 5e ^ {- t} $ จะเป็นศูนย์ tหมายถึงอินฟินิตี้ ดังนั้นนี่คือไฟล์transient term. และเทอมแรก 10 ยังคงเป็นtเข้าใกล้อินฟินิตี้ ดังนั้นนี่คือไฟล์steady state term.
สัญญาณทดสอบมาตรฐาน
สัญญาณทดสอบมาตรฐาน ได้แก่ แรงกระตุ้นขั้นตอนทางลาดและพาราโบลา สัญญาณเหล่านี้ใช้เพื่อทราบประสิทธิภาพของระบบควบคุมโดยใช้เวลาตอบสนองของเอาต์พุต
สัญญาณอิมพัลส์ยูนิต
สัญญาณอิมพัลส์ยูนิตδ (t) ถูกกำหนดให้เป็น
$ \ delta (t) = 0 $ สำหรับ $ t \ neq 0 $
และ $ \ int_ {0 ^ -} ^ {0 ^ +} \ delta (t) dt = 1 $
รูปต่อไปนี้แสดงสัญญาณอิมพัลส์ของหน่วย

ดังนั้นสัญญาณอิมพัลส์ของหน่วยจึงมีอยู่ที่ 't' เท่ากับศูนย์เท่านั้น พื้นที่ของสัญญาณนี้ภายใต้ช่วงเวลาเล็ก ๆ รอบ 't' เท่ากับศูนย์คือหนึ่ง ค่าของสัญญาณอิมพัลส์หน่วยเป็นศูนย์สำหรับค่าอื่น ๆ ทั้งหมดของ 't'
สัญญาณขั้นตอนของหน่วย
สัญญาณขั้นตอนหน่วย u (t) ถูกกำหนดให้เป็น
$$ u (t) = 1; t \ geq 0 $$
$ = 0; t <0 $
รูปต่อไปนี้แสดงสัญญาณขั้นตอนของหน่วย

ดังนั้นสัญญาณขั้นตอนหน่วยจึงมีอยู่สำหรับค่าบวกทั้งหมดของ 't' รวมถึงศูนย์ และค่าของมันคือหนึ่งในช่วงเวลานี้ ค่าของสัญญาณขั้นตอนของหน่วยเป็นศูนย์สำหรับค่าลบทั้งหมดของ 't'
สัญญาณทางลาดของหน่วย
สัญญาณทางลาดของหน่วย r (t) ถูกกำหนดให้เป็น
$$ r (t) = เสื้อ; t \ geq 0 $$
$ = 0; t <0 $
เราสามารถเขียน unit ramp signal, $ r (t) $ ในรูปของ unit step signal, $ u (t) $ as
$$ r (t) = tu (t) $$
รูปต่อไปนี้แสดงสัญญาณทางลาดของยูนิต

ดังนั้นสัญญาณทางลาดของหน่วยจึงมีอยู่สำหรับค่าบวกทั้งหมดของ 't' รวมถึงศูนย์ และค่าของมันจะเพิ่มขึ้นในเชิงเส้นเมื่อเทียบกับ 't' ในช่วงเวลานี้ ค่าของสัญญาณหน่วยลาดเป็นศูนย์สำหรับค่าลบทั้งหมดของ 't'
สัญญาณพาราโบลาของหน่วย
สัญญาณพาราโบลาหน่วย p (t) หมายถึง
$$ p (t) = \ frac {t ^ 2} {2}; t \ geq 0 $$
$ = 0; t <0 $
เราสามารถเขียนสัญญาณพาราโบลาหน่วย, $ p (t) $ ในรูปของสัญญาณขั้นหน่วย, $ u (t) $ as,
$$ p (t) = \ frac {t ^ 2} {2} u (t) $$
รูปต่อไปนี้แสดงสัญญาณพาราโบลาของหน่วย
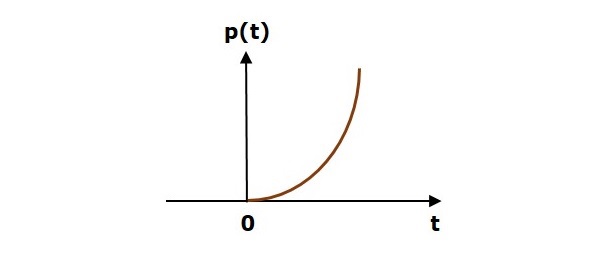
ดังนั้นสัญญาณพาราโบลาของหน่วยจึงมีอยู่สำหรับค่าบวกทั้งหมดของ ‘t’รวมถึงศูนย์ และค่าของมันจะเพิ่มขึ้นแบบไม่เป็นเชิงเส้นเมื่อเทียบกับ 't' ในช่วงเวลานี้ ค่าของสัญญาณพาราโบลาของหน่วยเป็นศูนย์สำหรับค่าลบทั้งหมดของ 't'