ระบบควบคุม - พล็อตลาง
พล็อต Bode หรือแผนภาพ Bode ประกอบด้วยสองแปลง -
- พล็อตขนาด
- พล็อตเฟส
ในทั้งสองแปลงแกน x แสดงความถี่เชิงมุม (มาตราส่วนลอการิทึม) ในขณะที่แอกซิสแสดงถึงขนาด (สเกลเชิงเส้น) ของฟังก์ชันการถ่ายโอนลูปเปิดในพล็อตขนาดและมุมเฟส (สเกลเชิงเส้น) ของฟังก์ชันการถ่ายโอนลูปเปิดในพล็อตเฟส
magnitude ของฟังก์ชันการถ่ายโอนลูปเปิดใน dB คือ -
$$ M = 20 \: \ log | G (j \ omega) H (j \ omega) | $$
phase angle ของฟังก์ชันการถ่ายโอนลูปเปิดในองศาคือ -
$$ \ phi = \ angle G (j \ omega) H (j \ omega) $$
Note - ฐานของลอการิทึมคือ 10
พื้นฐานของ Bode Plots
ตารางต่อไปนี้แสดงความชันขนาดและค่ามุมเฟสของเงื่อนไขที่มีอยู่ในฟังก์ชันการถ่ายโอนลูปเปิด ข้อมูลนี้มีประโยชน์ขณะวาด Bode plot
| ประเภทของคำ | G (j) H (jω) | ความลาดชัน (dB / Dec) | ขนาด (dB) | มุมเฟส (องศา) |
|---|---|---|---|---|
คงที่ |
$ K $ |
$ 0 $ |
$ 20 \ log K $ |
$ 0 $ |
ศูนย์ที่จุดกำเนิด |
$ j \ omega $ |
$ 20 $ |
$ 20 \ log \ omega $ |
$ 90 $ |
'n' ศูนย์ที่จุดกำเนิด |
$ (j \ omega) ^ n $ |
$ 20 \: n $ |
$ 20 \: n \ log \ โอเมก้า $ |
$ 90 \: n $ |
เสาต้นกำเนิด |
$ \ frac {1} {j \ omega} $ |
$ -20 $ |
$ -20 \ log \ omega $ |
$ -90 \: หรือ \: 270 $ |
'n' เสาต้นกำเนิด |
$ \ frac {1} {(j \ omega) ^ n} $ |
$ -20 \: n $ |
$ -20 \: n \ log \ โอเมก้า $ |
$ -90 \: n \: หรือ \: 270 \: n $ |
ศูนย์ง่าย |
$ 1 + j \ omega r $ |
$ 20 $ |
$ 0 \: สำหรับ \: \ omega <\ frac {1} {r} $ $ 20 \: \ log \ โอเมก้า r \: for \: \ omega> \ frac {1} {r} $ |
$ 0 \: สำหรับ \: \ omega <\ frac {1} {r} $ $ 90 \: สำหรับ \: \ omega> \ frac {1} {r} $ |
เสาธรรมดา |
$ \ frac {1} {1 + j \ omega r} $ |
$ -20 $ |
$ 0 \: สำหรับ \: \ omega <\ frac {1} {r} $ $ -20 \: \ log \ โอเมก้า r \: สำหรับ \: \ โอเมก้า> \ frac {1} {r} $ |
$ 0 \: สำหรับ \: \ omega <\ frac {1} {r} $ $ -90 \: หรือ \: 270 \: สำหรับ \: \ omega> \ frac {1} {r} $ |
อนุพันธ์ลำดับที่สอง |
$ \ omega_n ^ 2 \ left (1- \ frac {\ omega ^ 2} {\ omega_n ^ 2} + \ frac {2j \ delta \ omega} {\ omega_n} \ right) $ |
$ 40 $ |
$ 40 \: \ log \: \ omega_n \: สำหรับ \: \ omega <\ omega_n $ $ 20 \: \ log \ :( 2 \ delta \ omega_n ^ 2) \: สำหรับ \: \ omega = \ omega_n $ $ 40 \: \ log \: \ omega \: สำหรับ \: \ omega> \ omega_n $ |
$ 0 \: สำหรับ \: \ omega <\ omega_n $ $ 90 \: สำหรับ \: \ omega = \ omega_n $ $ 180 \: สำหรับ \: \ omega> \ omega_n $ |
คำสั่งที่สอง |
$ \ frac {1} {\ omega_n ^ 2 \ left (1- \ frac {\ omega ^ 2} {\ omega_n ^ 2} + \ frac {2j \ delta \ omega} {\ omega_n} \ right)} $ |
$ -40 $ |
$ -40 \: \ log \: \ omega_n \: สำหรับ \: \ omega <\ omega_n $ $ -20 \: \ log \ :( 2 \ delta \ omega_n ^ 2) \: สำหรับ \: \ omega = \ omega_n $ $ -40 \: \ log \: \ omega \: สำหรับ \: \ omega> \ omega_n $ |
$ -0 \: สำหรับ \: \ omega <\ omega_n $ $ -90 \: สำหรับ \: \ omega = \ omega_n $ $ -180 \: สำหรับ \: \ omega> \ omega_n $ |
พิจารณาฟังก์ชันการถ่ายโอนลูปเปิด $ G (s) H (s) = K $
ขนาด $ M = 20 \: \ log K $ dB
มุมเฟส $ \ phi = 0 $ องศา
ถ้า $ K = 1 $ ขนาดคือ 0 dB
ถ้า $ K> 1 $ ขนาดจะเป็นบวก
ถ้า $ K <1 $ ขนาดจะเป็นลบ
รูปต่อไปนี้แสดงพล็อต Bode ที่เกี่ยวข้อง


พล็อตขนาดเป็นเส้นแนวนอนซึ่งไม่ขึ้นกับความถี่ เส้น 0 dB คือพล็อตขนาดเมื่อค่าของ K เท่ากับหนึ่ง สำหรับค่าบวกของ K เส้นแนวนอนจะเลื่อน $ 20 \: \ log K $ dB เหนือเส้น 0 dB สำหรับค่าลบของ K เส้นแนวนอนจะเลื่อน $ 20 \: \ log K $ dB ใต้เส้น 0 dB เส้นศูนย์องศานั้นเป็นพล็อตเฟสสำหรับค่าบวกทั้งหมดของ K
พิจารณาฟังก์ชันการโอนลูปเปิด $ G (s) H (s) = s $
ขนาด $ M = 20 \ log \ omega $ dB
มุมเฟส $ \ phi = 90 ^ 0 $
ที่ $ \ omega = 0.1 $ rad / วินาทีขนาดคือ -20 dB
ที่ $ \ omega = 1 $ rad / วินาทีขนาดคือ 0 dB
ที่ $ \ omega = 10 $ rad / วินาทีขนาดคือ 20 dB
รูปต่อไปนี้แสดงพล็อต Bode ที่เกี่ยวข้อง


พล็อตขนาดคือเส้นซึ่งมีความชัน 20 dB / Dec เส้นนี้เริ่มต้นที่ $ \ omega = 0.1 $ rad / วินาทีโดยมีขนาด -20 dB และต่อไปบนความชันเดียวกัน กำลังแตะเส้น 0 dB ที่ $ \ omega = 1 $ rad / วินาที ในกรณีนี้พล็อตเฟสคือ 90 0บรรทัด
พิจารณาฟังก์ชันการถ่ายโอนลูปเปิด $ G (s) H (s) = 1 + s \ tau $
ขนาด $ M = 20 \: log \ sqrt {1 + \ omega ^ 2 \ tau ^ 2} $ dB
มุมเฟส $ \ phi = \ tan ^ {- 1} \ โอเมก้า \ tau $ องศา
สำหรับ $ ω <\ frac {1} {\ tau} $ ขนาดคือ 0 dB และมุมเฟสคือ 0 องศา
ราคา $ \ omega> \ frac {1} {\ tau} $ ขนาดเป็น $ 20 \: \ Log \ omega \ tau $ เดซิเบลและมุมเฟส 90 0
รูปต่อไปนี้แสดงพล็อต Bode ที่เกี่ยวข้อง

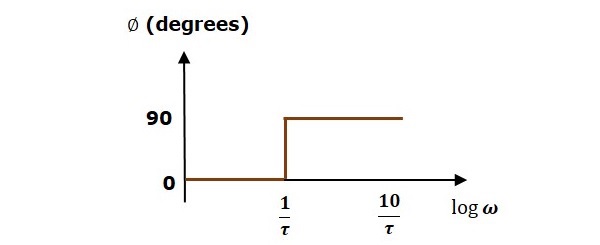
พล็อตขนาดมีขนาด 0 dB สูงถึง $ \ omega = \ frac {1} {\ tau} $ rad / วินาที จาก $ \ omega = \ frac {1} {\ tau} $ rad / วินาทีมีความชัน 20 dB / Dec ในกรณีนี้พล็อตเฟสจะมีมุมเฟส 0 องศาถึง $ \ omega = \ frac {1} {\ tau} $ RAD / วินาทีและจากที่นี่ก็จะมีมุมเฟส 90 0 พล็อต Bode นี้เรียกว่าasymptotic Bode plot.
เนื่องจากขนาดและเฟสพล็อตแสดงด้วยเส้นตรงพล็อต Exact Bode จึงมีลักษณะคล้ายกับพล็อต Asymptotic Bode ข้อแตกต่างเพียงอย่างเดียวคือพล็อต Exact Bode จะมีเส้นโค้งที่เรียบง่ายแทนที่จะเป็นเส้นตรง
ในทำนองเดียวกันคุณสามารถวาดพล็อต Bode สำหรับเงื่อนไขอื่น ๆ ของฟังก์ชันการถ่ายโอนลูปเปิดซึ่งระบุไว้ในตาราง