Netzwerktheorie - Gekoppelte Schaltungen
Ein Stromkreis soll a sein coupled circuit, wenn zwischen den in dieser Schaltung vorhandenen Spulen (oder Induktivitäten) eine gegenseitige Induktivität besteht. Die Spule ist nichts anderes als die Reihenkombination aus Widerstand und Induktivität. In Abwesenheit eines Widerstands wird die Spule zum Induktor. Manchmal werden die Begriffe Spule und Induktor synonym verwendet.
Lassen Sie uns in diesem Kapitel zuerst die Punktkonvention und dann die Klassifizierung der Kopplung diskutieren.
Dot Convention
Die Punktkonvention ist eine Technik, die Details zur Spannungspolarität am gepunkteten Anschluss angibt. Diese Informationen sind beim Schreiben von KVL-Gleichungen hilfreich.
Wenn der Strom am gepunkteten Anschluss einer Spule (oder Induktivität) eintritt, induziert er eine Spannung an einer anderen Spule (oder Induktivität), die hat positive polarity am gepunkteten Terminal.
Wenn der Strom vom gepunkteten Anschluss einer Spule (oder Induktivität) abfließt, induziert er eine Spannung an einer anderen Spule (oder Induktivität), die vorhanden ist negative polarity am gepunkteten Terminal.
Klassifizierung der Kupplung
Wir können klassifizieren coupling in die folgenden zwei Kategorien.
- Elektrische Kupplung
- Magnetkupplung
Lassen Sie uns nun nacheinander über jede Art der Kopplung sprechen.
Elektrische Kupplung
Eine elektrische Kopplung tritt auf, wenn eine vorhanden ist physical connectionzwischen zwei Spulen (oder Induktivitäten). Diese Kupplung kann entweder vom unterstützenden Typ oder vom entgegengesetzten Typ sein. Es basiert darauf, ob der Strom am gepunkteten Anschluss eintritt oder vom gepunkteten Anschluss austritt.
Kupplung vom Typ Aiding
Betrachten Sie den folgenden Stromkreis, in dem zwei Induktoren angeschlossen sind series.
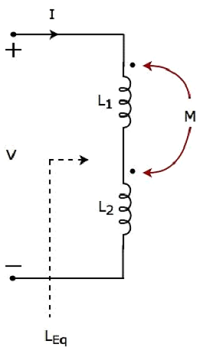
Da die beiden Induktivitäten in Reihe geschaltet sind, wird die same current IDurchfluss durch beide Induktivitäten mit Selbstinduktivitäten L 1 und L 2 .
In diesem Fall tritt der Strom am gepunkteten Anschluss jedes Induktors ein. Daher wird die induzierte Spannung in jedem Induktor habenpositive polarity am gepunkteten Anschluss aufgrund des in einer anderen Spule fließenden Stroms.
Anwenden KVL um die Schleife des obigen Stromkreises oder Netzwerks.
$$ V - L_1 \ frac {dI} {dt} - M \ frac {dI} {dt} - L_2 \ frac {dI} {dt} - M \ frac {dI} {dt} = 0 $$
$$ V = L_1 \ frac {dI} {dt} + L_2 \ frac {dI} {dt} + 2M \ frac {dI} {dt} $$
$$ V = (L_1 + L_2 + 2M) \ frac {dI} {dt} $$
Die obige Gleichung hat die Form von $ \ mathbf {\ mathit {V = L_ {Gl.} \ Frac {dI} {dt}}} $
deshalb, die equivalent inductance der in der obigen Abbildung gezeigten Reihenkombination von Induktoren ist
$$ L_ {Gl.} = L_1 + L_2 + 2M $$
In diesem Fall wurde die äquivalente Induktivität um 2 M erhöht. Daher ist die obige elektrische Schaltung ein Beispiel fürelectrical Kupplung, die von ist aiding Art.
Kupplung des entgegengesetzten Typs
Betrachten Sie den folgenden Stromkreis, in dem zwei Induktoren angeschlossen sind series.
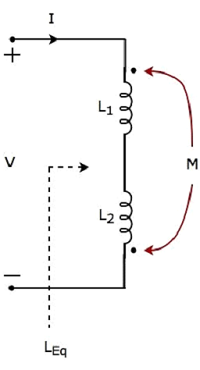
In der obigen Schaltung ist der Strom I tritt am gepunkteten Anschluss des Induktors mit einer Induktivität von ein L1. Daher induziert es eine Spannung in dem anderen Induktor mit einer Induktivität vonL2. Damit,positive polarity der induzierten Spannung liegt am gepunkteten Anschluss dieses Induktors an.
In der obigen Schaltung ist der Strom I Blätter vom gepunkteten Anschluss des Induktors mit einer Induktivität von L2. Daher induziert es eine Spannung in dem anderen Induktor mit einer Induktivität vonL1. Damit,negative polarity der induzierten Spannung liegt am gepunkteten Anschluss dieses Induktors an.
Anwenden KVL um die Schleife des obigen Stromkreises oder Netzwerks.
$$ V - L_1 \ frac {dI} {dt} + M \ frac {dI} {dt} - L_2 \ frac {dI} {dt} + M \ frac {dI} {dt} = 0 $$
$$ \ Rightarrow V = L_1 \ frac {dI} {dt} + L_2 \ frac {dI} {dt} - 2M \ frac {dI} {dt} $$
$$ \ Rightarrow V = (L_1 + L_2 - 2M) \ frac {dI} {dt} $$
Die obige Gleichung hat die Form von $ \ mathbf {\ mathit {V = L_ {Gl.} \ Frac {dI} {dt}}} $
deshalb, die equivalent inductance der in der obigen Abbildung gezeigten Reihenkombination von Induktoren ist
$$ L_ {Gl.} = L_1 + L_2 - 2M $$
In diesem Fall wurde die äquivalente Induktivität um 2 M verringert. Daher ist die obige elektrische Schaltung ein Beispiel fürelectrical Kupplung, die von ist opposing Art.
Magnetkupplung
Wenn vorhanden, tritt eine magnetische Kopplung auf no physical connectionzwischen zwei Spulen (oder Induktivitäten). Diese Kupplung kann entweder vom unterstützenden Typ oder vom entgegengesetzten Typ sein. Es basiert darauf, ob der Strom am gepunkteten Anschluss eintritt oder vom gepunkteten Anschluss austritt.
Kupplung vom Typ Aiding
Betrachten Sie das folgende elektrische Äquivalent circuit of transformer. Es hat zwei Spulen und diese werden als Primär- und Sekundärspulen bezeichnet.
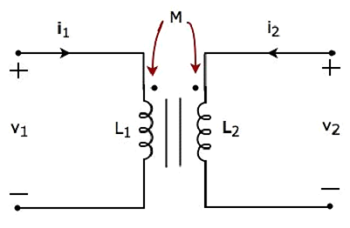
Die durch Primär- und Sekundärspulen fließenden Ströme betragen i 1 bzw. i 2 . In diesem Fall sind diese Strömeenteram gepunkteten Anschluss der jeweiligen Spule. Daher hat die induzierte Spannung in jeder Spule aufgrund des in einer anderen Spule fließenden Stroms am gepunkteten Anschluss eine positive Polarität.
Anwenden KVL um die Primärspule.
$$ v_1 - L_1 \ frac {d i_1} {dt} - M \ frac {d i_2} {dt} = 0 $$
$ \ Rightarrow v_1 = L_1 \ frac {d i_1} {dt} + M \ frac {d i_2} {dt} $Equation 1
Anwenden KVL um die Sekundärspule.
$$ v_2 - L_2 \ frac {d i_2} {dt} - M \ frac {d i_1} {dt} = 0 $$
$ \ Rightarrow v_2 = L_2 \ frac {d i_2} {dt} + M \ frac {d i_1} {dt} $Equation 2
In Gleichung 1 und Gleichung 2 haben die selbstinduzierte Spannung und die gegenseitig induzierte Spannung die gleiche Polarität. Daher ist die obige Transformatorschaltung ein Beispiel fürmagnetic coupling, das ist von aiding Art.
Kopplung des entgegengesetzten Typs
Betrachten Sie das folgende elektrische Äquivalent circuit of transformer.

Die durch Primär- und Sekundärspulen fließenden Ströme betragen i 1 bzw. i 2 . In diesem Fall tritt der Strom i 1 am gepunkteten Anschluss der Primärspule ein. Daher induziert es eine Spannung in der Sekundärspule. Damit,positive polarity der induzierten Spannung liegt am gepunkteten Anschluss dieser Sekundärspule an.
In der obigen Schaltung verlässt der Strom i 2 den gepunkteten Anschluss der Sekundärspule. Daher induziert es eine Spannung in der Primärspule. Damit,negative polarity der induzierten Spannung liegt am gepunkteten Anschluss dieser Primärspule an.
Anwenden KVL um die Primärspule.
$$ v_1 - L_1 \ frac {d i_1} {dt} + M \ frac {d i_2} {dt} = 0 $$
$ \ Rightarrow v_1 = L_1 \ frac {d i_1} {dt} - M \ frac {d i_2} {dt} $Equation 3
Anwenden KVL um die Sekundärspule.
$$ v_2 - L_2 \ frac {d i_2} {dt} + M \ frac {d i_1} {dt} = 0 $$
$ \ Rightarrow v_2 = L_2 \ frac {d i_2} {dt} - M \ frac {d i_1} {dt} $Equation 4
In Gleichung 3 und Gleichung 4 haben die selbstinduzierte Spannung und die gegenseitig induzierte Spannung eine entgegengesetzte Polarität. Daher ist die obige Transformatorschaltung ein Beispiel fürmagnetic coupling, das ist von opposing Art.