Prinzipien der Aufteilung der elektrischen Mengen
Lassen Sie uns in diesem Kapitel die folgenden zwei Teilungsprinzipien elektrischer Größen diskutieren.
- Aktuelles Teilungsprinzip
- Prinzip der Spannungsteilung
Aktuelles Teilungsprinzip
Wenn zwei oder mehr passive Elemente parallel geschaltet sind, wird die Strommenge, die durch jedes Element fließt, erhalten divided (gemeinsam) untereinander aus dem Strom, der in den Knoten eintritt.
Folgendes berücksichtigen circuit diagram.
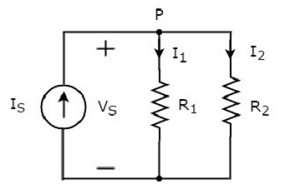
Das obige Schaltbild besteht aus einer Eingangsstromquelle IS parallel zu zwei Widerständen R1 und R2. Die Spannung an jedem Element beträgtVS. Die durch die Widerstände fließenden StrömeR1 und R2 sind I1 und I2 beziehungsweise.
Das KCL equation am Knoten P wird sein
$$ I_S = I_1 + I_2 $$
Ersetzen Sie $ I_1 = \ frac {V_S} {R_1} $ und $ I_2 = \ frac {V_S} {R_2} $ in der obigen Gleichung.
$$ I_S = \ frac {V_S} {R_1} + \ frac {V_S} {R_2} = V_S \ lgroup \ frac {R_2 + R_1} {R_1 R_2} \ rgroup $$
$$ \ Rightarrow V_S = I_S \ lgroup \ frac {R_1R_2} {R_1 + R_2} \ rgroup $$
Ersetzen Sie den Wert von V S durch $ I_1 = \ frac {V_S} {R_1} $.
$$ I_1 = \ frac {I_S} {R_1} \ lgroup \ frac {R_1 R_2} {R_1 + R_2} \ rgroup $$
$$ \ Rightarrow I_1 = I_S \ lgroup \ frac {R_2} {R_1 + R_2} \ rgroup $$
Ersetzen Sie den Wert von V S durch $ I_2 = \ frac {V_S} {R_2} $.
$$ I_2 = \ frac {I_S} {R_2} \ lgroup \ frac {R_1 R_2} {R_1 + R_2} \ rgroup $$
$$ \ Rightarrow I_2 = I_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
Aus den Gleichungen von I 1 und I 2 können wir verallgemeinern, dass der durch jedes passive Element fließende Strom unter Verwendung der folgenden Formel gefunden werden kann.
$$ I_N = I_S \ lgroup \ frac {Z_1 \ rVert Z_2 \ rVert ... \ rVert Z_ {N-1}} {Z_1 + Z_2 + ... + Z_N} \ rgroup $$
Dies ist bekannt als current division principle und es ist anwendbar, wenn zwei oder mehr passive Elemente parallel geschaltet sind und nur ein Strom in den Knoten eintritt.
Wo,
I N ist der Strom, der durch das passive Element des N- ten Zweigs fließt .
I S ist der Eingangsstrom, der in den Knoten eintritt.
Z 1 , Z 2 , ..., Z N sind die Impedanzen von 1 st Zweig, 2 nd Zweig, ..., N - ten Zweig verbunden.
Prinzip der Spannungsteilung
Wenn zwei oder mehr passive Elemente in Reihe geschaltet sind, wird die an jedem Element vorhandene Spannungsmenge erhalten divided (geteilt) untereinander aus der Spannung, die über diese gesamte Kombination verfügbar ist.
Folgendes berücksichtigen circuit diagram.
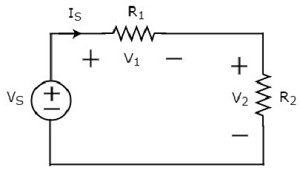
Das obige Schaltbild besteht aus einer Spannungsquelle V S in Reihe mit zwei Widerständen R 1 und R 2 . Der Strom fließt durch diese Elemente ist I S . Die Spannungsabfälle an den Widerständen R 1 und R 2 betragen V 1 bzw. V 2 .
Das KVL equation um die Schleife wird sein
$$ V_S = V_1 + V_2 $$
Ersetzen Sie V 1 = I S R 1 und V 2 = I S R 2 in der obigen Gleichung
$$ V_S = I_S R_1 + I_S R_2 = I_S (R_1 + R_2) $$
$$ I_S = \ frac {V_S} {R_1 + R_2} $$
Ersetzen Sie den Wert von I S durch V 1 = I S R 1 .
$$ V_1 = \ lgroup \ frac {V_S} {R_1 + R_2} \ rgroup R_1 $$
$$ \ Rightarrow V_1 = V_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
Ersetzen Sie den Wert von I S durch V 2 = I S R 2 .
$$ V_2 = \ lgroup \ frac {V_S} {R_1 + R_2} \ rgroup R_2 $$
$$ \ Rightarrow V_2 = V_S \ lgroup \ frac {R_2} {R_1 + R_2} \ rgroup $$
Aus den Gleichungen von V 1 und V 2 können wir verallgemeinern, dass die Spannung an jedem passiven Element unter Verwendung der folgenden Formel ermittelt werden kann.
$$ V_N = V_S \ lgroup \ frac {Z_N} {Z_1 + Z_2 + .... + Z_N} \ rgroup $$
Dies ist bekannt als voltage division principle und es ist anwendbar, wenn zwei oder mehr passive Elemente in Reihe geschaltet sind und nur eine Spannung über die gesamte Kombination verfügbar ist.
Wo,
V N ist die Spannung am N- ten passiven Element.
V S ist die Eingangsspannung, die über die gesamte Kombination von passiven Serienelementen anliegt.
Z 1 , Z 2 , ..., Z 3 sind die Impedanzen von 1 st passivem Elemente, 2 nd passiven Element, ..., N - ten passiven Element verbunden.