Netzwerktheorie - Kirchhoffs Gesetze
Netzwerkelemente können eines von beiden sein active oder passiveArt. Jeder Stromkreis oder jedes Netzwerk enthält einen dieser beiden Arten von Netzwerkelementen oder eine Kombination aus beiden.
Lassen Sie uns nun über die folgenden zwei Gesetze diskutieren, die im Volksmund als bekannt sind Kirchhoff’s laws.
- Kirchhoffs aktuelles Gesetz
- Kirchhoffs Spannungsgesetz
Kirchhoffs aktuelles Gesetz
Kirchhoffs aktuelles Gesetz (KCL) besagt, dass die algebraische Summe der Ströme, die einen Knoten verlassen (oder in diesen eintreten), gleich Null ist.
EIN Nodeist ein Punkt, an dem zwei oder mehr Schaltungselemente damit verbunden sind. Wenn nur zwei Schaltungselemente mit einem Knoten verbunden sind, spricht man von einem einfachen Knoten. Wenn drei oder mehr Schaltungselemente mit einem Knoten verbunden sind, spricht man von einem KnotenPrincipal Node.
Mathematically, KCL kann dargestellt werden als
$$ \ displaystyle \ sum \ limit_ {m = 1} ^ M I_m = 0 $$
Wo,
Imist der m- te Zweigstrom, der den Knoten verlässt.
M ist die Anzahl der Zweige, die mit einem Knoten verbunden sind.
Die obige Aussage von KCLkann auch ausgedrückt werden als "die algebraische Summe von Strömen, die in einen Knoten eintreten, ist gleich der algebraischen Summe von Strömen, die einen Knoten verlassen". Lassen Sie uns diese Aussage anhand des folgenden Beispiels überprüfen.
Beispiel
Schreiben KCL equation am Knoten P der folgenden Abbildung.
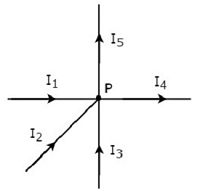
In der obigen Abbildung, die Zweigströme I 1 , I 2 und I 3 sindentering Betrachten Sie also negative Vorzeichen für diese drei Ströme.
In der obigen Abbildung, die Zweigströme I 4 und I 5 sindleaving Betrachten Sie also positive Vorzeichen für diese beiden Ströme.
Das KCL equation am Knoten P wird sein
$$ - I_1 - I_2 - I_3 + I_4 + I_5 = 0 $$
$$ \ Rightarrow I_1 + I_2 + I_3 = I_4 + I_5 $$
In der obigen Gleichung repräsentiert die linke Seite die Summe der eintretenden Ströme, während die rechte Seite die Summe der austretenden Ströme darstellt.
In diesem Tutorial betrachten wir das positive Vorzeichen, wenn der Strom einen Knoten verlässt, und das negative Vorzeichen, wenn er in einen Knoten eintritt. Ebenso können Sie ein negatives Vorzeichen berücksichtigen, wenn der Strom einen Knoten verlässt, und ein positives Vorzeichen, wenn er in einen Knoten eintritt. In beiden Fällen ist dieresult will be same.
Note - KCL ist unabhängig von der Art der Netzwerkelemente, die mit einem Knoten verbunden sind.
Kirchhoffs Spannungsgesetz
Das Kirchhoffsche Spannungsgesetz (KVL) besagt, dass die algebraische Summe der Spannungen um eine Schleife oder ein Netz gleich Null ist.
EIN Loopist ein Pfad, der an demselben Knoten endet, von dem aus er gestartet wurde. Im Gegensatz dazu aMesh ist eine Schleife, die keine anderen Schleifen enthält.
Mathematisch kann KVL als dargestellt werden
$$ \ displaystyle \ sum \ limit_ {n = 1} ^ N V_n = 0 $$
Wo,
Vnist die Spannung des n- ten Elements in einer Schleife (Masche).
N ist die Anzahl der Netzwerkelemente in der Schleife (Netz).
Die obige Aussage von KVLkann auch ausgedrückt werden als "die algebraische Summe der Spannungsquellen ist gleich der algebraischen Summe der Spannungsabfälle, die in einer Schleife vorhanden sind." Lassen Sie uns diese Aussage anhand des folgenden Beispiels überprüfen.
Beispiel
Schreiben KVL equation um die Schleife der folgenden Schaltung.
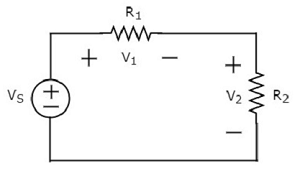
Das obige Schaltbild besteht aus einer Spannungsquelle V S in Reihe mit zwei Widerständen R 1 und R 2 . Die Spannungsabfälle an den Widerständen R 1 und R 2 betragen V 1 bzw. V 2 .
Anwenden KVL um die Schleife.
$$ V_S - V_1 - V_2 = 0 $$
$$ \ Rightarrow V_S = V_1 + V_2 $$
In der obigen Gleichung repräsentiert der Term auf der linken Seite eine einzelne Spannungsquelle VS. Während die rechte Seite die darstelltsum of voltage drops. In diesem Beispiel haben wir nur eine Spannungsquelle betrachtet. Deshalb enthält die linke Seite nur einen Begriff. Wenn wir mehrere Spannungsquellen betrachten, enthält die linke Seite die Summe der Spannungsquellen.
In diesem Tutorial betrachten wir das Vorzeichen der Spannung jedes Elements als die Polarität des zweiten Anschlusses, der während der Fahrt um die Schleife vorhanden ist. In ähnlicher Weise können Sie das Vorzeichen jeder Spannung als die Polarität des ersten Anschlusses betrachten, der vorhanden ist, während Sie sich um die Schleife bewegen. In beiden Fällen ist dieresult will be same.
Note - KVL ist unabhängig von der Art der Netzwerkelemente, die in einer Schleife vorhanden sind.