Netzwerktheorie - Knotenanalyse
Es gibt zwei grundlegende Methoden, die zum Lösen eines elektrischen Netzwerks verwendet werden: Nodal analysis und Mesh analysis. Lassen Sie uns in diesem Kapitel über dieNodal analysis Methode.
In der Knotenanalyse werden wir die Knotenspannungen in Bezug auf Masse berücksichtigen. Daher wird die Knotenanalyse auch als bezeichnetNode-voltage method.
Verfahren der Knotenanalyse
Befolgen Sie diese Schritte, während Sie ein elektrisches Netzwerk oder einen Stromkreis mithilfe der Knotenanalyse lösen.
Step 1 - Identifizieren Sie die principal nodes und wählen Sie eine davon als reference node. Wir werden diesen Referenzknoten als Grund behandeln.
Step 2 - Beschriften Sie die node voltages in Bezug auf Masse von allen Hauptknoten mit Ausnahme des Referenzknotens.
Step 3 - Schreiben nodal equationsan allen Hauptknoten außer dem Referenzknoten. Die Knotengleichung wird erhalten, indem zuerst KCL und dann das Ohmsche Gesetz angewendet werden.
Step 4 - Lösen Sie die in Schritt 3 erhaltenen Knotengleichungen, um die Knotenspannungen zu erhalten.
Jetzt können wir den durch jedes Element fließenden Strom und die Spannung über jedem Element, das in dem gegebenen Netzwerk vorhanden ist, unter Verwendung von Knotenspannungen finden.
Beispiel
Finden Sie den Strom, der durch den 20 Ω-Widerstand der folgenden Schaltung fließt, mit Nodal analysis.
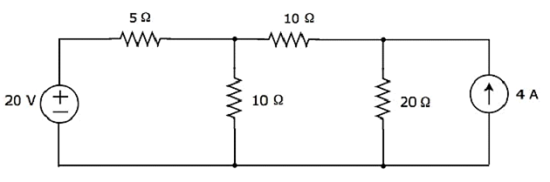
Step 1 - Es gibt three principle nodesin der obigen Schaltung. Diese sind in der folgenden Abbildung mit 1, 2 und 3 gekennzeichnet.
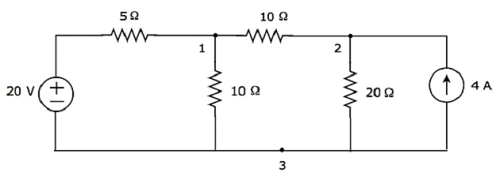
Betrachten Sie in der obigen Abbildung node 3 als Referenzknoten (Masse).
Step 2- Die Knotenspannungen V 1 und V 2 sind in der folgenden Abbildung gekennzeichnet.
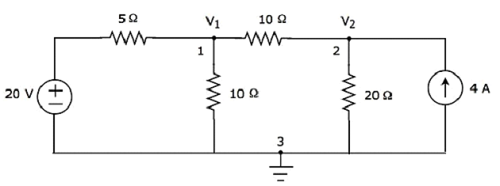
In der obigen Figur ist V 1 die Spannung von Knoten 1 in Bezug auf Masse und V 2 ist die Spannung von Knoten 2 in Bezug auf Masse.
Step 3 - In diesem Fall werden wir bekommen two nodal equations, da es außer Masse zwei Hauptknoten gibt, 1 und 2. Wenn wir die Knotengleichungen an einem Knoten schreiben, nehmen wir an, dass alle Ströme von dem Knoten ausgehen, für den die Stromrichtung nicht erwähnt wird, und dass die Spannung dieses Knotens größer ist als die anderer Knotenspannungen in der Schaltung.
Das nodal equation am Knoten 1 ist
$$ \ frac {V_1 - 20} {5} + \ frac {V_1} {10} + \ frac {V_1 - V_2} {10} = 0 $$
$$ \ Rightarrow \ frac {2 V_1 - 40 + V_1 + V_1 - V_2} {10} = 0 $$
$$ \ Rightarrow 4V_1 - 40 - V_2 = 0 $$
$ \ Rightarrow V_2 = 4V_1 - 40 $ Equation 1
Das nodal equation am Knoten 2 ist
$$ - 4 + \ frac {V_2} {20} + \ frac {V_2 - V_1} {10} = 0 $$
$$ \ Rightarrow \ frac {-80 + V_2 + 2V_2 - 2V_2} {20} = 0 $$
$ \ Rightarrow 3V_2 - 2V_1 = 80 $ Equation 2
Step 4- Finden der Knotenspannungen V 1 und V 2 durch Lösen von Gleichung 1 und Gleichung 2.
Ersetzen Sie Gleichung 1 in Gleichung 2.
$$ 3 (4 V_1 - 40) - 2 V_1 = 80 $$
$$ \ Rightarrow 12 V_1 - 120 - 2V_1 = 80 $$
$$ \ Rightarrow 10 V_1 = 200 $$
$$ \ Rightarrow V_1 = 20V $$
Ersetzen Sie V 1 = 20 V in Gleichung 1.
$$ V_2 = 4 (20) - 40 $$
$$ \ Rightarrow V_2 = 40V $$
Wir haben also die Knotenspannungen V 1 und V 2 als20 V und 40 V beziehungsweise.
Step 5- Die Spannung am 20 Ω-Widerstand ist nichts anderes als die Knotenspannung V 2 und beträgt 40 V. Jetzt können wir den durch den 20 Ω-Widerstand fließenden Strom unter Verwendung des Ohmschen Gesetzes ermitteln.
$$ I_ {20 \ Omega} = \ frac {V_2} {R} $$
Ersetzen Sie die Werte von V 2 und R in der obigen Gleichung.
$$ I_ {20 \ Omega} = \ frac {40} {20} $$
$$ \ Rightarrow I_ {20 \ Omega} = 2A $$
Daher beträgt der Strom, der durch den 20 Ω-Widerstand einer gegebenen Schaltung fließt 2 A.
Note- Aus dem obigen Beispiel können wir schließen, dass wir 'n' Knotengleichungen lösen müssen, wenn der Stromkreis 'n' Hauptknoten hat (außer dem Referenzknoten). Daher können wir die Knotenanalyse wählen, wenn dienumber of principal nodes (außer Referenzknoten) ist kleiner als die Anzahl der Maschen eines Stromkreises.