Netzwerktopologiematrizen
Im vorherigen Kapitel haben wir erläutert, wie ein Stromkreis in einen äquivalenten Graphen umgewandelt wird. Lassen Sie uns nun die Netzwerktopologiematrizen diskutieren, die zur Lösung von Stromkreisen oder Netzwerkproblemen mithilfe ihrer entsprechenden Diagramme nützlich sind.
Mit Netzwerkgraphen verknüpfte Matrizen
Es folgen die drei Matrizen, die in der Graphentheorie verwendet werden.
- Inzidenzmatrix
- Grundlegende Schleifenmatrix
- Fundamental Cut Set Matrix
Inzidenzmatrix
Eine Inzidenzmatrix repräsentiert den Graphen eines bestimmten Stromkreises oder Netzwerks. Daher ist es möglich, den Graphen desselben Stromkreises oder Netzwerks aus dem zu zeichnenincidence matrix.
Wir wissen, dass der Graph aus einer Reihe von Knoten besteht und diese durch einige Zweige verbunden sind. Das Verbinden von Zweigen mit einem Knoten wird daher als Inzidenz bezeichnet. Die Inzidenzmatrix wird mit dem Buchstaben A dargestellt. Sie wird auch als Knoten-zu-Verzweigungs-Inzidenzmatrix oder bezeichnetnode incidence matrix.
Wenn es 'n' Knoten gibt und 'b' Zweige in a vorhanden sind directed graphDann hat die Inzidenzmatrix 'n' Zeilen und 'b' Spalten. Hier entsprechen Zeilen und Spalten den Knoten und Zweigen eines gerichteten Graphen. Daher dieorder der Inzidenzmatrix wird sein n × b.
Das elements of incidence matrix wird einen dieser drei Werte haben, +1, -1 und 0.
Wenn der Zweigstrom von einem ausgewählten Knoten abfließt, beträgt der Wert des Elements +1.
Wenn der Verzweigungsstrom in Richtung eines ausgewählten Knotens fließt, ist der Wert des Elements -1.
Wenn der Verzweigungsstrom weder an einem ausgewählten Knoten eintritt noch von einem ausgewählten Knoten austritt, ist der Wert des Elements 0.
Verfahren zum Auffinden der Inzidenzmatrix
Befolgen Sie diese Schritte, um die Inzidenzmatrix des gerichteten Graphen zu ermitteln.
Wählen Sie einen Knoten zu einem Zeitpunkt des angegebenen gerichteten Graphen aus und füllen Sie die Werte der Elemente der Inzidenzmatrix, die diesem Knoten entsprechen, in einer Reihe aus.
Wiederholen Sie den obigen Schritt für alle Knoten des angegebenen gerichteten Graphen.
Beispiel
Folgendes berücksichtigen directed graph.

Das incidence matrix entsprechend dem oben gerichteten Graphen wird
$$ A = \ begin {bmatrix} -1 & 1 & 0 & -1 & 0 & 0 \\ 0 & -1 & 1 & 0 & 1 & 0 \\ 1 & 0 & -1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & -1 & -1 \ end {bmatrix} $$
Die Zeilen und Spalten der obigen Matrix repräsentieren die Knoten und Zweige eines gegebenen gerichteten Graphen. Die Reihenfolge dieser Inzidenzmatrix ist 4 × 6.
Durch Beobachtung der obigen Inzidenzmatrix können wir schließen, dass die summationder Spaltenelemente der Inzidenzmatrix ist gleich Null. Das heißt, ein Zweigstrom verlässt einen Knoten und tritt nur an einem anderen einzelnen Knoten ein.
Note- Wenn das angegebene Diagramm ein nicht gerichteter Typ ist, konvertieren Sie es in ein gerichtetes Diagramm, indem Sie die Pfeile auf jedem Zweig davon darstellen. Wir können die beliebige Richtung des Stromflusses in jedem Zweig berücksichtigen.
Grundlegende Schleifenmatrix
Grundschleife oder f-loopist eine Schleife, die nur einen Link und einen oder mehrere Zweige enthält. Die Anzahl der f-Schleifen entspricht also der Anzahl der Verbindungen. Die Grundschleifenmatrix wird mit dem Buchstaben B dargestellt. Sie wird auch als bezeichnetfundamental circuit matrixund Tie-Set-Matrix. Diese Matrix gibt die Beziehung zwischen Zweigströmen und Verbindungsströmen an.
Wenn es 'n' Knoten gibt und 'b' Zweige in a vorhanden sind directed graphDann ist die Anzahl der in einem Co-Baum vorhandenen Links, die dem ausgewählten Baum eines gegebenen Graphen entspricht, b-n + 1.
Die Grundschleifenmatrix hat also 'b-n + 1' Zeilen und 'b' Spalten. Hier entsprechen Zeilen und Spalten den Verknüpfungen von Co-Tree und Zweigen eines bestimmten Graphen. Daher ist die Reihenfolge der Grundschleifenmatrix(b - n + 1) × b.
Das elements of fundamental loop matrix wird einen dieser drei Werte haben, +1, -1 und 0.
Der Wert des Elements ist +1 für die Verknüpfung der ausgewählten f-Schleife.
Der Wert der Elemente ist 0 für die verbleibenden Links und Zweige, die nicht Teil der ausgewählten f-Schleife sind.
Wenn die Richtung des Zweigstroms der ausgewählten f-Schleife dieselbe ist wie die des Verbindungsstroms der f-Schleife, ist der Wert des Elements +1.
Wenn die Richtung des Zweigstroms der ausgewählten f-Schleife der Richtung des f-Schleifen-Verbindungsstroms entgegengesetzt ist, ist der Wert des Elements -1.
Vorgehensweise zum Auffinden der Fundamental Loop Matrix
Befolgen Sie diese Schritte, um die Grundschleifenmatrix eines bestimmten gerichteten Graphen zu finden.
Wählen Sie einen Baum eines bestimmten gerichteten Graphen aus.
Wenn Sie jeweils einen Link einfügen, erhalten Sie eine f-Schleife. Füllen Sie die Werte der Elemente, die dieser f-Schleife entsprechen, in eine Reihe der Grundschleifenmatrix.
Wiederholen Sie den obigen Schritt für alle Links.
Beispiel
Schauen Sie sich den folgenden Baum an directed graph, die für die Inzidenzmatrix berücksichtigt wird.

Der obige Baum enthält drei Zweige d, e & f. Daher sind die Zweige a, b und c die Verknüpfungen des Co-Baums, die dem obigen Baum entsprechen. Wenn Sie jeweils einen Link zum obigen Baum einfügen, erhalten Sie einenf-loop. Es werden also drei seinf-loops, da es drei links gibt. Diese drei f-Schleifen sind in der folgenden Abbildung dargestellt.
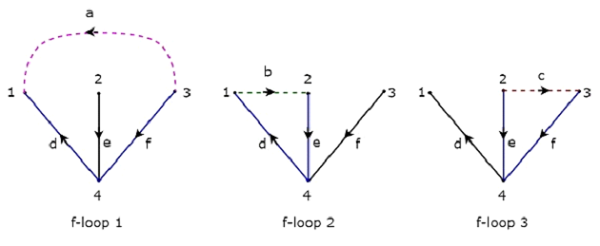
In der obigen Abbildung bilden die Zweige, die mit farbigen Linien dargestellt sind, f-Schleifen. Wir erhalten die zeilenweisen Elementwerte der Tie-Set-Matrix aus jeder f-Schleife. Also, dieTieset matrix des oben betrachteten Baumes wird sein
$$ B = \ begin {bmatrix} 1 & 0 & 0 & -1 & 0 & -1 \\ 0 & 1 & 0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & -1 & 1 \ end {bmatrix} $$
Die Zeilen und Spalten der obigen Matrix repräsentieren die Verknüpfungen und Zweige eines gegebenen gerichteten Graphen. Die Reihenfolge dieser Inzidenzmatrix ist 3 × 6.
Das number of Fundamental loop matriceseines gerichteten Graphen entspricht der Anzahl der Bäume dieses gerichteten Graphen. Weil jeder Baum eine Grundschleifenmatrix hat.
Grundlegende Cut-Set-Matrix
Grundschnitt oder f-cut setist die Mindestanzahl von Zweigen, die so aus einem Diagramm entfernt werden, dass das ursprüngliche Diagramm zu zwei isolierten Untergraphen wird. Das F-Cut-Set enthält nurone twigund einen oder mehrere Links. Die Anzahl der F-Cut-Sets entspricht also der Anzahl der Zweige.
Fundamental cut set matrix wird mit dem Buchstaben C dargestellt. Diese Matrix gibt die Beziehung zwischen Zweigspannungen und Zweigspannungen an.
Wenn es 'n' Knoten gibt und 'b' Zweige in a vorhanden sind directed graphDann ist die Anzahl der in einem ausgewählten Baum eines bestimmten Graphen vorhandenen Zweige n-1. Die grundlegende Schnittmengenmatrix hat also 'n-1' Zeilen und 'b' Spalten. Hier entsprechen Zeilen und Spalten den Zweigen des ausgewählten Baums und den Zweigen eines bestimmten Diagramms. Daher dieorder der fundamentalen Schnittmenge Matrix wird sein (n-1) × b.
Das elements of fundamental cut set matrix wird einen dieser drei Werte haben, +1, -1 und 0.
Der Wert des Elements beträgt +1 für den Zweig des ausgewählten f-Cutset.
Der Wert der Elemente ist 0 für die verbleibenden Zweige und Links, die nicht Teil des ausgewählten f-Cutset sind.
Wenn die Richtung des Verbindungsstroms des ausgewählten F-Cut-Sets mit der des F-Cutset-Zweigstroms übereinstimmt, beträgt der Wert des Elements +1.
Wenn die Richtung des Verbindungsstroms des ausgewählten f-Schnitt-Satzes der des f-Schnitt-Zweigstroms entgegengesetzt ist, ist der Wert des Elements -1.
Vorgehensweise zum Auffinden der Fundamental Cut-Set Matrix
Befolgen Sie diese Schritte, um die grundlegende Schnittmengenmatrix eines bestimmten gerichteten Graphen zu finden.
Wählen Sie einen Baum mit einem bestimmten gerichteten Diagramm aus und stellen Sie die Verknüpfungen mit den gepunkteten Linien dar.
Wenn Sie jeweils einen Zweig und die erforderlichen Links entfernen, erhalten Sie einen F-Cut-Satz. Füllen Sie die Werte der Elemente, die diesem F-Schnitt-Satz entsprechen, in eine Reihe grundlegender Schnitt-Satz-Matrix.
Wiederholen Sie den obigen Schritt für alle Zweige.
Beispiel
Betrachten Sie das gleiche directed graph , die wir im Abschnitt der Inzidenzmatrix besprochen haben. Wählen Sie die Zweige d, e & f dieses gerichteten Graphen als Zweige aus. Die verbleibenden Zweige a, b und c dieses gerichteten Graphen sind also die Verknüpfungen.
Das twigs d, e & f sind mit durchgezogenen Linien und dargestellt links a, b & c sind in der folgenden Abbildung mit gepunkteten Linien dargestellt.
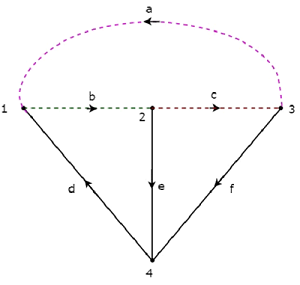
Wenn Sie jeweils einen Zweig und die erforderlichen Links entfernen, erhalten Sie einen F-Cut-Satz. Es wird also drei F-Cut-Sets geben, da es drei Zweige gibt. Diese dreif-cut sets sind in der folgenden Abbildung dargestellt.

Wir werden drei F-Cut-Sätze haben, indem wir einen Satz Zweige und Glieder von C 1 , C 2 und C 3 entfernen . Wir erhalten die zeilenweisen Elementwerte der fundamentalen Schnittmengenmatrix aus jeder f-Schnittmenge. Also, diefundamental cut set matrix des oben betrachteten Baumes wird sein
$$ C = \ begin {bmatrix} 1 & -1 & 0 & 1 & 0 & 0 \\ 0 & -1 & 1 & 0 & 1 & 0 \\ 1 & 0 & -1 & 0 & 0 & 1 \ end {bmatrix} $$
Die Zeilen und Spalten der obigen Matrix repräsentieren die Zweige und Zweige eines gegebenen gerichteten Graphen. Die Reihenfolge dieser fundamentalen Schnittmengenmatrix ist 3 × 6.
Das number of Fundamental cut set matriceseines gerichteten Graphen entspricht der Anzahl der Bäume dieses gerichteten Graphen. Weil jeder Baum eine fundamentale Schnittmengenmatrix hat.