Netzwerktheorie - Serienresonanz
Resonancetritt in elektrischen Schaltkreisen aufgrund des Vorhandenseins von Energiespeicherelementen wie Induktor und Kondensator auf. Es ist das grundlegende Konzept, auf dessen Grundlage die Radio- und Fernsehempfänger so ausgelegt sind, dass sie nur die gewünschte Senderfrequenz auswählen können.
Es gibt two typesvon Resonanzen, nämlich Serienresonanz und Parallelresonanz. Diese werden anhand der Netzwerkelemente klassifiziert, die in Reihe oder parallel geschaltet sind. Lassen Sie uns in diesem Kapitel die Serienresonanz diskutieren.
Serienresonanz-Schaltplan
Wenn die Resonanz in einer Reihen-RLC-Schaltung auftritt, wird sie als bezeichnet Series Resonance. Folgendes berücksichtigenseries RLC circuit, die in der Zeigerdomäne dargestellt wird.
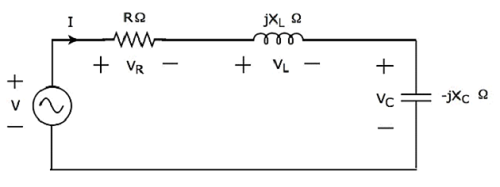
Hier sind die passiven Elemente wie Widerstand, Induktivität und Kondensator in Reihe geschaltet. Diese gesamte Kombination ist inseries mit der sinusförmigen Eingangsspannungsquelle.
Anwenden KVL um die Schleife.
$$ V - V_R - V_L - V_C = 0 $$
$$ \ Rightarrow V - IR - I (j X_L) - I (-j X_C) = 0 $$
$$ \ Rightarrow V = IR + I (j X_L) + I (-j X_C) $$
$ \ Rightarrow V = I [R + j (X_L - X_C)] $Equation 1
Die obige Gleichung hat die Form von V = IZ.
deshalb, die impedance Z der Serie RLC-Schaltung wird sein
$$ Z = R + j (X_L - X_C) $$
Parameter und elektrische Größen bei Resonanz
Lassen Sie uns nun die Werte der Parameter und elektrischen Größen bei Resonanz der Serien-RLC-Schaltung nacheinander ableiten.
Resonanzfrequenz
Die Frequenz, bei der Resonanz auftritt, wird als bezeichnet resonant frequency fr. In der Serie RLC tritt eine Resonanz auf, wenn der imaginäre Term der Impedanz Z Null ist, dh der Wert von $ X_L - X_C $ sollte gleich Null sein.
$$ \ Rightarrow X_L = X_C $$
Ersetzen Sie $ X_L = 2 \ pi f L $ und $ X_C = \ frac {1} {2 \ pi f C} $ in der obigen Gleichung.
$$ 2 \ pi f L = \ frac {1} {2 \ pi f C} $$
$$ \ Rightarrow f ^ 2 = \ frac {1} {(2 \ pi) ^ 2 LC} $$
$$ \ Rightarrow f = \ frac {1} {(2 \ pi) \ sqrt {LC}} $$
deshalb, die resonant frequency fr der Serie RLC-Schaltung ist
$$ f_r = \ frac {1} {(2 \ pi) \ sqrt {LC}} $$
Wo, L ist die Induktivität eines Induktors und C ist die Kapazität eines Kondensators.
Das resonant frequency fr der Serien-RLC-Schaltung hängt nur von der Induktivität ab L und Kapazität C. Aber es ist unabhängig vom WiderstandR.
Impedanz
Wir haben die impedance Z der Serien-RLC-Schaltung als
$$ Z = R + j (X_L - X_C) $$
Ersetzen Sie $ X_L = X_C $ in der obigen Gleichung.
$$ Z = R + j (X_C - X_C) $$
$$ \ Rightarrow Z = R + j (0) $$
$$ \ Rightarrow Z = R $$
Bei Resonanz wird die impedance Z der Serien-RLC-Schaltung ist gleich dem Widerstandswert Rdh Z = R.
Strom fließt durch den Stromkreis
Ersetzen Sie $ X_L - X_C = 0 $ in Gleichung 1.
$$ V = I [R + j (0)] $$
$$ \ Rightarrow V = IR $$
$$ \ Rightarrow I = \ frac {V} {R} $$
Deshalb, current Das Durchfließen der Serien-RLC-Schaltung bei Resonanz ist $ \ mathbf {\ mathit {I = \ frac {V} {R}}} $.
Bei Resonanz erreicht die Impedanz der Serien-RLC-Schaltung einen Minimalwert. Daher diemaximum current fließt durch diesen Stromkreis bei Resonanz.
Spannung am Widerstand
Die Spannung am Widerstand beträgt
$$ V_R = IR $$
Ersetzen Sie den Wert von I in der obigen Gleichung.
$$ V_R = \ lgroup \ frac {V} {R} \ rgroup R $$
$$ \ Rightarrow V_R = V $$
deshalb, die voltage across resistor bei Resonanz ist VR = V.
Spannung am Induktor
Die Spannung am Induktor beträgt
$$ V_L = I (jX_L) $$
Ersetzen Sie den Wert von I in der obigen Gleichung.
$$ V_L = \ lgroup \ frac {V} {R} \ rgroup (jX_L) $$
$$ \ Rightarrow V_L = j \ lgroup \ frac {X_L} {R} \ rgroup V $$
$$ \ Rightarrow V_L = j QV $$
deshalb, die voltage across inductor bei Resonanz ist $ V_L = j QV $.
Also, die magnitude der Spannung über Induktor bei Resonanz wird sein
$$ | V_L | = QV $$
Wo Q ist der Quality factor und sein Wert ist gleich $ \ frac {X_L} {R} $
Spannung am Kondensator
Die Spannung am Kondensator beträgt
$$ V_C = I (-j X_C) $$
Ersetzen Sie den Wert von I in der obigen Gleichung.
$$ V_C = \ lgroup \ frac {V} {R} \ rgroup (-j X_C) $$
$$ \ Rightarrow V_C = -j \ lgroup \ frac {X_C} {R} \ rgroup V $$
$$ \ Rightarrow V_C = -jQV $$
deshalb, die voltage across capacitor bei Resonanz ist $ \ mathbf {\ mathit {V_C = -jQV}} $.
Also, die magnitude der Spannung über dem Kondensator bei Resonanz wird
$$ | V_C | = QV $$
Wo Q ist der Quality factor und sein Wert ist gleich $ \ frac {X_ {C}} {R} $
Note - Die Serienresonanz-RLC-Schaltung wird als bezeichnet voltage magnificationSchaltung, weil die Größe der Spannung über der Induktivität und dem Kondensator gleich dem Q- fachen der sinusförmigen Eingangsspannung V ist .