Netzwerktheorie - Thevenins Theorem
Thevenin’s theoremgibt an, dass ein beliebiges lineares Netzwerk oder eine Schaltung mit zwei Anschlüssen mit einem äquivalenten Netzwerk oder einer äquivalenten Schaltung dargestellt werden kann, die aus einer Spannungsquelle in Reihe mit einem Widerstand besteht. Es ist als Thevenins Ersatzschaltbild bekannt. Eine lineare Schaltung kann unabhängige Quellen, abhängige Quellen und Widerstände enthalten.
Wenn die Schaltung mehrere unabhängige Quellen, abhängige Quellen und Widerstände enthält, kann die Antwort in einem Element leicht gefunden werden, indem das gesamte Netzwerk links von diesem Element durch a ersetzt wird Thevenin’s equivalent circuit.
Das response in an element kann die Spannung an diesem Element, der durch dieses Element fließende Strom oder die an diesem Element abgegebene Leistung sein.
Dieses Konzept ist in den folgenden Abbildungen dargestellt.
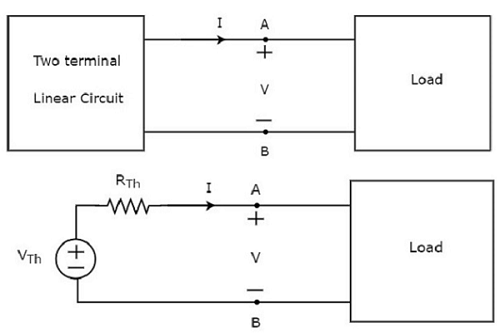
Thevenin’s equivalent circuitähnelt einer praktischen Spannungsquelle. Daher hat es eine Spannungsquelle in Reihe mit einem Widerstand.
Die im Ersatzschaltbild des Thevenin vorhandene Spannungsquelle wird als Ersatzschaltbild des Thevenin oder einfach bezeichnet Thevenin’s voltage, VTh.
Der im Ersatzschaltbild des Thevenin vorhandene Widerstand wird als Ersatzwiderstand des Thevenin oder einfach bezeichnet Thevenin’s resistor, RTh.
Methoden zum Auffinden des Thevenin-Ersatzschaltbilds
Es gibt drei Methoden, um ein Thevenin-Ersatzschaltbild zu finden. Basierend auftype of sourcesdie im Netzwerk vorhanden sind, können wir eine dieser drei Methoden wählen. Lassen Sie uns nun zwei Methoden einzeln diskutieren. Wir werden die dritte Methode im nächsten Kapitel diskutieren.
Methode 1
Befolgen Sie diese Schritte, um das Ersatzschaltbild des Thevenin zu finden, wenn nur das sources of independent type sind anwesend.
Step 1 - Betrachten Sie den Schaltplan, indem Sie die Klemmen öffnen, zu denen das Ersatzschaltbild des Thevenin zu finden ist.
Step 2 - Finden Sie die Spannung von Thevenin VTh über die offenen Klemmen der obigen Schaltung.
Step 3 - Finde Thevenins Widerstand RTh über die offenen Anschlüsse der obigen Schaltung durch Eliminieren der darin vorhandenen unabhängigen Quellen.
Step 4 - Zeichne die Thevenin’s equivalent circuitdurch Verbinden einer Thevenin-Spannung V Th in Reihe mit einem Thevenin-Widerstand R Th .
Jetzt können wir die Antwort in einem Element finden, das auf der rechten Seite von Thevenins Ersatzschaltbild liegt.
Beispiel
Finden Sie den Strom, der durch den 20 Ω-Widerstand fließt, indem Sie zuerst a finden Thevenin’s equivalent circuit links von den Klemmen A und B.
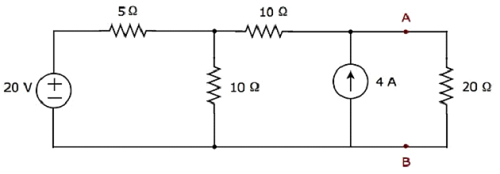
Step 1 - Um das Ersatzschaltbild des Thevenin auf der linken Seite der Klemmen A und B zu finden, sollten wir den 20-Ω-Widerstand durch aus dem Netzwerk entfernen opening the terminals A & B. Das modifizierte Schaltbild ist in der folgenden Abbildung dargestellt.
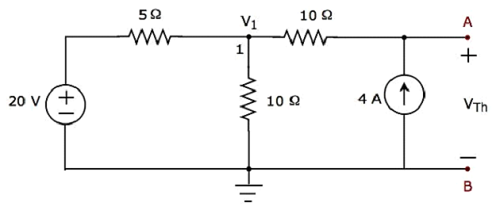
Step 2 - Berechnung von Thevenin’s voltage VTh.
Es gibt nur einen Hauptknoten außer Masse in der obigen Schaltung. Also können wir verwendennodal analysisMethode. Die Knotenspannung V 1 und die Thevenin-Spannung V Th sind in der obigen Figur gekennzeichnet. Hier ist V 1 die Spannung von Knoten 1 in Bezug auf Masse und V Th ist die Spannung an einer 4 A-Stromquelle.
Das nodal equation am Knoten 1 ist
$$ \ frac {V_1 - 20} {5} + \ frac {V_1} {10} - 4 = 0 $$
$$ \ Rightarrow \ frac {2V_1 - 40 + V_1 - 40} {10} = 0 $$
$$ \ Rightarrow 3V_1 - 80 = 0 $$
$$ \ Rightarrow V_1 = \ frac {80} {3} V $$
Die Spannung am 10 Ω-Widerstand des Serienzweigs beträgt
$$ V_ {10 \ Omega} = (-4) (10) = -40 V $$
In der obigen Schaltung gibt es zwei Maschen. DasKVL equation um das zweite Netz ist
$$ V_1 - V_ {10 \ Omega} - V_ {Th} = 0 $$
Ersetzen Sie die Werte von $ V_1 $ und $ V_ {10 \ Omega} $ in der obigen Gleichung.
$$ \ frac {80} {3} - (-40) - V_ {Th} = 0 $$
$$ V_ {Th} = \ frac {80 + 120} {3} = \ frac {200} {3} V $$
Daher beträgt die Spannung des Thevenin $ V_ {Th} = \ frac {200} {3} V $
Step 3 - Berechnung von Thevenin’s resistance RTh.
Schließen Sie die Spannungsquelle kurz und unterbrechen Sie die Stromquelle des obigen Stromkreises, um den Thevenin-Widerstand R Th über die Klemmen A und B zu berechnenmodified circuit diagram ist in der folgenden Abbildung dargestellt.
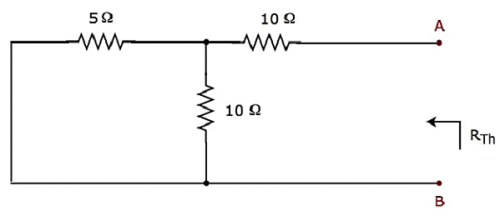
Der Widerstand des Thevenin über die Klemmen A und B wird sein
$$ R_ {Th} = \ lgroup \ frac {5 \ times 10} {5 + 10} \ rgroup + 10 = \ frac {10} {3} + 10 = \ frac {40} {3} \ Omega $$
Daher ist der Widerstand des Thevenin $ \ mathbf {R_ {Th} = \ frac {40} {3} \ Omega} $.
Step 4- Das Ersatzschaltbild des Thevenin befindet sich links von den Klemmen A und B im angegebenen Schaltkreis. Dieses Schaltbild ist in der folgenden Abbildung dargestellt.

Der durch den 20 Ω-Widerstand fließende Strom kann durch Ersetzen der Werte von V Th , R Th und R in der folgenden Gleichung ermittelt werden.
$$ l = \ frac {V_ {Th}} {R_ {Th} + R} $$
$$ l = \ frac {\ frac {200} {3}} {\ frac {40} {3} + 20} = \ frac {200} {100} = 2A $$
Daher beträgt der durch den 20 Ω-Widerstand fließende Strom 2 A.
Methode 2
Befolgen Sie diese Schritte, um das Ersatzschaltbild des Thevenin zu finden, wenn das sources of both independent type and dependent type sind anwesend.
Step 1 - Betrachten Sie den Schaltplan, indem Sie die Klemmen öffnen, für die sich das Ersatzschaltbild des Thevenin befindet.
Step 2 - Finden Sie die Spannung von Thevenin VTh über die offenen Klemmen der obigen Schaltung.
Step 3 - Finden Sie den Kurzschlussstrom ISC durch Kurzschließen der beiden geöffneten Anschlüsse des obigen Stromkreises.
Step 4 - Finde Thevenins Widerstand RTh unter Verwendung der folgenden Formel.
$$ R_ {Th} = \ frac {V_ {Th}} {I_ {SC}} $$
Step 5 - Zeichne die Thevenin’s equivalent circuitdurch Verbinden einer Thevenin-Spannung V Th in Reihe mit einem Thevenin-Widerstand R Th .
Jetzt können wir die Antwort in einem Element finden, das auf der rechten Seite des Thevenin-Ersatzschaltbilds liegt.