Netzwerktheorie - Kurzanleitung

Network theoryist die Untersuchung der Lösung der Probleme von Stromkreisen oder elektrischen Netzen. Lassen Sie uns in diesem Einführungskapitel zunächst die grundlegende Terminologie elektrischer Schaltkreise und die Arten von Netzwerkelementen erörtern.

Grundbegriffe

In der Netzwerktheorie werden wir häufig auf folgende Begriffe stoßen:

• Elektrischer Kreislauf
• Elektrisches Netz
• Current
• Voltage
• Power

Es ist daher unbedingt erforderlich, dass wir einige Grundkenntnisse zu diesen Begriffen sammeln, bevor wir fortfahren. Beginnen wir mit dem Stromkreis.

Elektrischer Kreislauf

Ein Stromkreis enthält einen geschlossenen Pfad zum Bereitstellen eines Elektronenflusses von einer Spannungsquelle oder Stromquelle. Die in einem Stromkreis vorhandenen Elemente befinden sich inseries connection, parallel connectionoder in einer beliebigen Kombination von Reihen- und Parallelschaltungen.

Elektrisches Netz

Ein elektrisches Netz muss keinen geschlossenen Pfad enthalten, um einen Elektronenfluss von einer Spannungsquelle oder Stromquelle bereitzustellen. Wir können daher den Schluss ziehen, dass "alle Stromkreise elektrische Netze sind", aber das Gegenteil muss nicht der Fall sein.

Aktuell

Die jetzige "I"Das Durchströmen eines Leiters ist nichts anderes als die zeitliche Geschwindigkeit des Ladungsflusses. Mathematisch kann es geschrieben werden als

$$I = \frac{dQ}{dt}$$

Wo,

• Q ist die Ladung und seine Einheit ist Coloumb.

• t ist die Zeit und ihre Einheit ist die Sekunde.

Als Analogie kann elektrischer Strom als Wasserfluss durch ein Rohr betrachtet werden. Der Strom wird gemessen inAmpere.

Im Allgemeinen, Electron current fließt vom negativen Anschluss der Quelle zum positiven Anschluss, wohingegen Conventional current fließt vom positiven Anschluss der Quelle zum negativen Anschluss.

Electron current wird aufgrund der Bewegung freier Elektronen erhalten, während Conventional currentwird aufgrund der Bewegung von freien positiven Ladungen erhalten. Beide werden als bezeichnetelectric current.

Stromspannung

Die Spannung "V"ist nichts anderes als eine elektromotorische Kraft, die bewirkt, dass die Ladung (Elektronen) fließt. Mathematisch kann es geschrieben werden als

$$V = \frac{dW}{dQ}$$

Wo,

• W ist die potentielle Energie und ihre Einheit ist Joule.

• Q ist die Ladung und seine Einheit ist Coloumb.

Als Analogie kann Spannung als Wasserdruck betrachtet werden, der bewirkt, dass das Wasser durch ein Rohr fließt. Es wird gemessen inVolt.

Leistung

Die Macht "P"ist nichts anderes als die zeitliche Flussrate elektrischer Energie. Mathematisch kann es geschrieben werden als

$$P = \frac{dW}{dt}$$

Wo,

• W ist die elektrische Energie und wird gemessen in Joule.

• t ist die Zeit und wird in Sekunden gemessen.

Wir können die obige Gleichung a neu schreiben

$$P = \frac{dW}{dt} = \frac{dW}{dQ} \times \frac{dQ}{dt} = VI$$

Deshalb, power ist nichts als das product der Spannung V und aktuell I. Seine Einheit istWatt.

Arten von Netzwerkelementen

Wir können die Netzwerkelemente basierend auf einigen Parametern in verschiedene Typen klassifizieren. Im Folgenden sind die Arten von Netzwerkelementen aufgeführt:

• Aktive und passive Elemente

• Lineare und nichtlineare Elemente

• Bilaterale Elemente und unilaterale Elemente

Aktive und passive Elemente

Wir können die Netzwerkelemente in beide klassifizieren active oder passive basierend auf der Fähigkeit, Energie zu liefern.

• Active Elementsandere Elemente, die in einem Stromkreis vorhanden sind, mit Strom versorgen. Manchmal absorbieren sie die Kraft wie passive Elemente. Das heißt, aktive Elemente können sowohl Energie liefern als auch absorbieren.Examples: Spannungsquellen und Stromquellen.

• Passive Elementskann anderen Elementen keine Energie liefern, sie können jedoch Energie absorbieren. Das heißt, diese Elemente leiten entweder Energie in Form von Wärme ab oder speichern Energie in Form eines Magnetfelds oder eines elektrischen Feldes.Examples: Widerstände, Induktivitäten und Kondensatoren.

Lineare und nichtlineare Elemente

Wir können die Netzwerkelemente als klassifizieren linear oder non-linear basierend auf ihrer Eigenschaft, der Eigenschaft der Linearität zu gehorchen.

• Linear Elements sind die Elemente, die eine lineare Beziehung zwischen Spannung und Strom zeigen. Examples: Widerstände, Induktivitäten und Kondensatoren.

• Non-Linear Elements sind solche, die keine lineare Beziehung zwischen Spannung und Strom zeigen. Examples: Spannungsquellen und Stromquellen.

Bilaterale Elemente und unilaterale Elemente

Netzwerkelemente können auch als solche klassifiziert werden bilateral oder unilateral basierend auf der Richtung des Stromflusses durch die Netzwerkelemente.

Bilateral Elements sind die Elemente, die den Strom in beide Richtungen zulassen und in beiden Richtungen des Stromflusses die gleiche Impedanz bieten. Examples: Widerstände, Induktivitäten und Kondensatoren.

Das Konzept der bilateralen Elemente ist in den folgenden Abbildungen dargestellt.

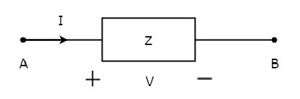
In der obigen Abbildung fließt der Strom (I) von den Klemmen A nach B durch ein passives Element mit einer Impedanz von Z Ω. Dies ist das Verhältnis der Spannung (V) über diesem Element zwischen den Klemmen A und B und dem Strom (I).

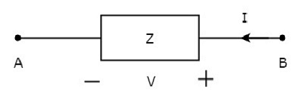
In der obigen Abbildung fließt der Strom (I) von den Anschlüssen B nach A durch ein passives Element mit einer Impedanz von Z Ω. Das heißt, der Strom (–I) fließt von den Klemmen A nach B. Auch in diesem Fall erhalten wir den gleichen Impedanzwert, da sowohl der Strom als auch die Spannung negative Vorzeichen in Bezug auf die Klemmen A und B haben.

Unilateral Elementssind solche, die den Strom nur in eine Richtung zulassen. Sie bieten daher unterschiedliche Impedanzen in beide Richtungen.

Wir haben die Arten von Netzwerkelementen im vorherigen Kapitel besprochen. Lassen Sie uns nun die identifizierennature of network elements aus den in den folgenden Beispielen angegebenen VI-Eigenschaften.

Beispiel 1

Das V-I characteristics eines Netzwerkelements ist unten gezeigt.

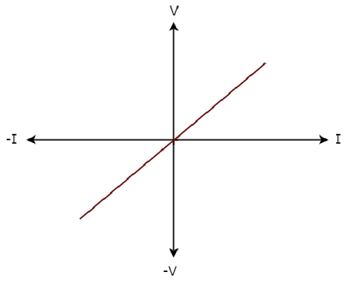
Step 1 - Überprüfen des Netzwerkelements als linear oder non-linear.

Aus der obigen Abbildung geht hervor, dass die VI-Eigenschaften eines Netzwerkelements eine gerade Linie sind, die durch den Ursprung verläuft. Daher ist es einLinear element.

Step 2 - Überprüfen des Netzwerkelements als active oder passive.

Die gegebenen VI-Eigenschaften eines Netzwerkelements liegen im ersten und dritten Quadranten.

• In dem first quadrantsind die Werte sowohl der Spannung (V) als auch des Stroms (I) positiv. Die Verhältnisse von Spannung (V) und Strom (I) ergeben also positive Impedanzwerte.

• Ebenso in der third quadranthaben die Werte sowohl der Spannung (V) als auch des Stroms (I) negative Werte. Die Verhältnisse von Spannung (V) und Strom (I) erzeugen also positive Impedanzwerte.

Da die gegebenen VI-Eigenschaften positive Impedanzwerte bieten, ist das Netzwerkelement a Passive element.

Step 3 - Überprüfen des Netzwerkelements als bilateral oder unilateral.

Für jeden Punkt (I, V) auf den Merkmalen existiert ein entsprechender Punkt (-I, -V) auf den gegebenen Merkmalen. Daher ist das Netzwerkelement aBilateral element.

Daher zeigen die angegebenen VI-Eigenschaften, dass das Netzwerkelement a ist Linear, Passive, und Bilateral element.

Beispiel 2

Das V-I characteristics eines Netzwerkelements ist unten gezeigt.

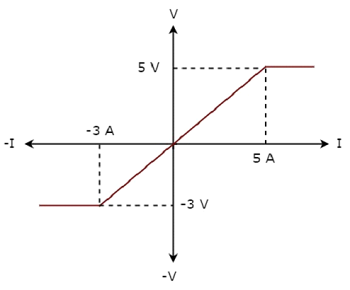
Step 1 - Überprüfen des Netzwerkelements als linear oder non-linear.

Aus der obigen Abbildung geht hervor, dass die VI-Eigenschaften eines Netzwerkelements nur zwischen den Punkten (-3A, -3V) und (5A, 5V) eine gerade Linie sind. Über diese Punkte hinaus folgen die VI-Eigenschaften nicht der linearen Beziehung. Daher ist es einNon-linear element.

Step 2 - Überprüfen des Netzwerkelements als active oder passive.

Die gegebenen VI-Eigenschaften eines Netzwerkelements liegen im ersten und dritten Quadranten. In diesen beiden Quadranten erzeugen die Verhältnisse von Spannung (V) und Strom (I) positive Impedanzwerte. Daher ist das Netzwerkelement aPassive element.

Step 3 - Überprüfen des Netzwerkelements als bilateral or unilateral.

Betrachten Sie den Punkt (5A, 5V) auf den Eigenschaften. Der entsprechende Punkt (-5A, -3V) liegt bei den angegebenen Eigenschaften anstelle von (-5A, -5V) vor. Daher ist das Netzwerkelement aUnilateral element.

Daher zeigen die angegebenen VI-Eigenschaften, dass das Netzwerkelement a ist Non-linear, Passive, und Unilateral element.

Active Elementssind die Netzwerkelemente, die andere Elemente in einem Stromkreis mit Strom versorgen. Aktive Elemente werden daher auch als Spannungs- oder Stromquellen bezeichnet. Wir können diese Quellen in die folgenden zwei Kategorien einteilen:

• Unabhängige Quellen
• Abhängige Quellen

Unabhängige Quellen

Wie der Name schon sagt, erzeugen unabhängige Quellen feste Spannungs- oder Stromwerte, die von keinem anderen Parameter abhängig sind. Unabhängige Quellen können weiter in die folgenden zwei Kategorien unterteilt werden:

• Unabhängige Spannungsquellen
• Unabhängige Stromquellen

Unabhängige Spannungsquellen

Eine unabhängige Spannungsquelle erzeugt an ihren beiden Anschlüssen eine konstante Spannung. Diese Spannung ist unabhängig von der Strommenge, die durch die beiden Anschlüsse der Spannungsquelle fließt.

Unabhängig ideal voltage source und seine VI-Eigenschaften sind in der folgenden Abbildung dargestellt.

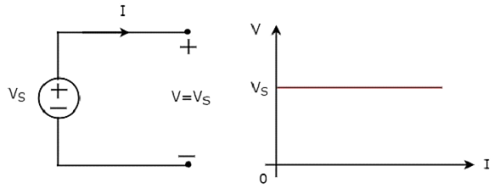
Das V-I characteristicseiner unabhängigen idealen Spannungsquelle ist eine konstante Leitung, die unabhängig vom Stromwert (I) immer gleich der Quellenspannung (VS) ist. Der Innenwiderstand einer unabhängigen idealen Spannungsquelle beträgt also null Ohm.

Daher die unabhängigen idealen Spannungsquellen do not exist practically, weil es einen gewissen Innenwiderstand geben wird.

Unabhängig practical voltage source und seine VI-Eigenschaften sind in der folgenden Abbildung dargestellt.

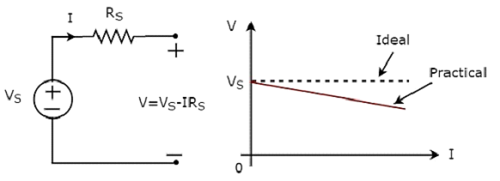
Es gibt eine Abweichung der VI-Eigenschaften einer unabhängigen praktischen Spannungsquelle von den VI-Eigenschaften einer unabhängigen idealen Spannungsquelle. Dies ist auf den Spannungsabfall über dem Innenwiderstand (R _S ) einer unabhängigen praktischen Spannungsquelle zurückzuführen.

Unabhängige Stromquellen

Eine unabhängige Stromquelle erzeugt einen konstanten Strom. Dieser Strom ist unabhängig von der Spannung an den beiden Klemmen. Unabhängigideal current source und seine VI-Eigenschaften sind in der folgenden Abbildung dargestellt.

Das V-I characteristicseiner unabhängigen idealen Stromquelle ist eine konstante Leitung, die unabhängig vom Spannungswert (V) immer gleich dem Quellenstrom (I _S ) ist. Der Innenwiderstand einer unabhängigen idealen Stromquelle beträgt also unendlich Ohm.

Daher die unabhängigen idealen Stromquellen do not exist practically, weil es einen gewissen Innenwiderstand geben wird.

Unabhängig practical current source und seine VI-Eigenschaften sind in der folgenden Abbildung dargestellt.

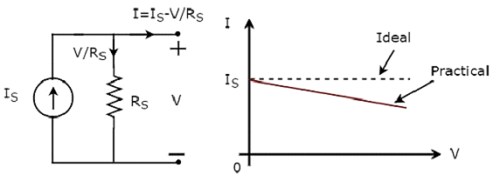
Die VI-Eigenschaften einer unabhängigen praktischen Stromquelle weichen von den VI-Eigenschaften einer unabhängigen idealen Stromquelle ab. Dies ist auf die Strommenge zurückzuführen, die durch den internen Nebenschlusswiderstand (R _S ) einer unabhängigen praktischen Stromquelle fließt .

Abhängige Quellen

Wie der Name schon sagt, erzeugen abhängige Quellen die Menge an Spannung oder Strom, die von einer anderen Spannung oder einem anderen Strom abhängig ist. Abhängige Quellen werden auch als bezeichnetcontrolled sources. Abhängige Quellen können weiter in die folgenden zwei Kategorien unterteilt werden:

• Abhängige Spannungsquellen
• Abhängige Stromquellen

Abhängige Spannungsquellen

Eine abhängige Spannungsquelle erzeugt an ihren beiden Anschlüssen eine Spannung. Die Höhe dieser Spannung hängt von einer anderen Spannung oder einem anderen Strom ab. Daher können abhängige Spannungsquellen weiter in die folgenden zwei Kategorien eingeteilt werden:

• Spannungsabhängige Spannungsquelle (VDVS)
• Stromabhängige Spannungsquelle (CDVS)

Abhängige Spannungsquellen werden mit den Zeichen '+' und '-' innerhalb einer Rautenform dargestellt. Die Größe der Spannungsquelle kann außerhalb der Rautenform dargestellt werden.

Abhängige Stromquellen

Eine abhängige Stromquelle erzeugt einen Strom. Die Höhe dieses Stroms hängt von einer anderen Spannung oder einem anderen Strom ab. Daher können abhängige Stromquellen weiter in die folgenden zwei Kategorien eingeteilt werden:

• Spannungsabhängige Stromquelle (VDCS)
• Stromabhängige Stromquelle (CDCS)

Abhängige Stromquellen werden mit einem Pfeil innerhalb einer Rautenform dargestellt. Die Größe der Stromquelle kann außerhalb der Diamantform dargestellt werden.

Wir können diese abhängigen oder gesteuerten Quellen in äquivalenten Transistormodellen beobachten.

Quellentransformationstechnik

Wir wissen, dass es zwei praktische Quellen gibt, nämlich voltage source und current source. Wir können je nach Anforderung eine Quelle in die andere umwandeln (konvertieren) und gleichzeitig Netzwerkprobleme lösen.

Die Technik, eine Quelle in die andere umzuwandeln, wird als bezeichnet source transformation technique. Es folgen die zwei möglichen Quellentransformationen -

• Praktische Spannungsquelle in eine praktische Stromquelle
• Praktische Stromquelle in eine praktische Spannungsquelle

Praktische Spannungsquelle in eine praktische Stromquelle

Die Umwandlung einer praktischen Spannungsquelle in eine praktische Stromquelle ist in der folgenden Abbildung dargestellt

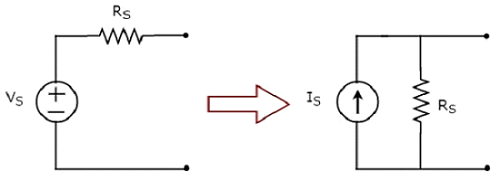
Practical voltage sourcebesteht aus einer Spannungsquelle (V _S ) in Reihe mit einem Widerstand (R _S ). Dies kann wie in der Abbildung gezeigt in eine praktische Stromquelle umgewandelt werden. Es besteht aus einer Stromquelle (I _S ) parallel zu einem Widerstand (R _S ).

Der Wert ist , wird auf das Verhältnis von V gleich _S und R _S . Mathematisch kann es dargestellt werden als

$$I_S = \frac{V_S}{R_S}$$

Praktische Stromquelle in eine praktische Spannungsquelle

Die Umwandlung einer praktischen Stromquelle in eine praktische Spannungsquelle ist in der folgenden Abbildung dargestellt.

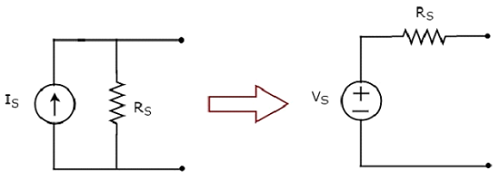
Die praktische Stromquelle besteht aus einer Stromquelle (I _S ) parallel zu einem Widerstand (R _S ). Dies kann wie in der Abbildung gezeigt in eine praktische Spannungsquelle umgewandelt werden. Es besteht aus einer Spannungsquelle (V _S ) in Reihe mit einem Widerstand (R _S ).

Der Wert von V _S wird zu dem Produkt von I gleich _S und R _S . Mathematisch kann es dargestellt werden als

$$V_S = I_S R_S$$

In diesem Kapitel werden wir die passiven Elemente wie Widerstand, Induktor und Kondensator ausführlich diskutieren. Beginnen wir mit Widerständen.

Widerstand

Die Hauptfunktionalität des Widerstands besteht darin, dem Stromfluss entweder entgegenzuwirken oder ihn einzuschränken. Daher werden die Widerstände verwendet, um den Stromfluss und / oder die Teilungsspannung zu begrenzen.

Der durch den Widerstand fließende Strom sei I Ampere und die Spannung über ihm beträgt V Volt. Dassymbol des Widerstands zusammen mit Strom I und Spannung V sind in der folgenden Abbildung dargestellt.

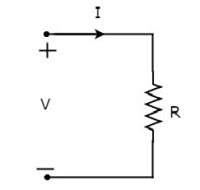
Gemäß Ohm’s lawDie Spannung am Widerstand ist das Produkt des durch ihn fließenden Stroms und des Widerstands dieses Widerstands. Mathematicallykann es dargestellt werden als

$V = IR$ Equation 1

$\Rightarrow I = \frac{V}{R}$Equation 2

Wo, R ist der Widerstand eines Widerstands.

Aus Gleichung 2 können wir schließen, dass der durch den Widerstand fließende Strom direkt proportional zur angelegten Spannung am Widerstand und umgekehrt proportional zum Widerstand des Widerstands ist.

Power in einem elektrischen Schaltungselement kann dargestellt werden als

$P = VI$Equation 3

Ersetzen Sie Gleichung 1 in Gleichung 3.

$P = (IR)I$

$\Rightarrow P = I^2 R$ Equation 4

Ersetzen Sie Gleichung 2 in Gleichung 3.

$P = V \lgroup \frac{V}{R} \rgroup$

$\Rightarrow P = \frac{V^2}{R}$ Equation 5

Wir können also die im Widerstand verbrauchte Leistung unter Verwendung einer der in den Gleichungen 3 bis 5 genannten Formeln berechnen.

Induktor

Im Allgemeinen haben Induktoren eine Anzahl von Windungen. Daher erzeugen sie einen magnetischen Fluss, wenn Strom durch sie fließt. Die Menge des gesamten magnetischen Flusses, der von einem Induktor erzeugt wird, hängt also von dem Strom ab, den ich durch ihn fließe, und sie haben eine lineare Beziehung.

Mathematicallykann geschrieben werden als

$$\Psi \: \alpha \: I$$

$$\Rightarrow \Psi = LI$$

Wo,

• Ψ ist der gesamte magnetische Fluss

• L ist die Induktivität eines Induktors

Der durch den Induktor fließende Strom sei I Ampere und die Spannung über ihm beträgt V Volt. Dassymbolder Induktivität zusammen mit Strom I und Spannung V sind in der folgenden Abbildung dargestellt.

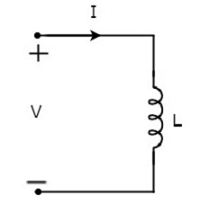
Gemäß Faraday’s lawkann die Spannung über der Induktivität wie folgt geschrieben werden

$$V = \frac{d\Psi}{dt}$$

Ersetzen Sie Ψ = LI in der obigen Gleichung.

$$V = \frac{d(LI)}{dt}$$

$$\Rightarrow V = L \frac{dI}{dt}$$

$$\Rightarrow I = \frac{1}{L} \int V dt$$

Aus den obigen Gleichungen können wir schließen, dass es eine gibt linear relationship zwischen der Spannung über der Induktivität und dem durch sie fließenden Strom.

Wir wissen das power in einem elektrischen Schaltungselement kann dargestellt werden als

$$P = VI$$

Ersatz $V = L \frac{dI}{dt}$ in der obigen Gleichung.

$$P = \lgroup L \frac{dI}{dt}\rgroup I$$

$$\Rightarrow P = LI \frac{dI}{dt}$$

Durch Integration der obigen Gleichung erhalten wir die energy in einem Induktor gespeichert als

$$W = \frac{1}{2} LI^2$$

Der Induktor speichert also die Energie in Form eines Magnetfeldes.

Kondensator

Im Allgemeinen hat ein Kondensator zwei leitende Platten, die durch ein dielektrisches Medium getrennt sind. Wenn eine positive Spannung an den Kondensator angelegt wird, speichert er positive Ladung. In ähnlicher Weise speichert eine negative Ladung, wenn eine negative Spannung an den Kondensator angelegt wird.

Die im Kondensator gespeicherte Ladungsmenge hängt also von der angelegten Spannung ab Vdarüber und sie haben eine lineare Beziehung. Mathematisch kann es geschrieben werden als

$$Q \: \alpha \: V$$

$$\Rightarrow Q = CV$$

Wo,

• Q ist die im Kondensator gespeicherte Ladung.

• C ist die Kapazität eines Kondensators.

Der durch den Kondensator fließende Strom sei I Ampere und die Spannung über ihm beträgt V Volt. Das Symbol des Kondensators zusammen mit Strom I und Spannung V ist in der folgenden Abbildung dargestellt.

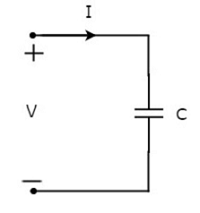
Wir wissen, dass die current ist nichts als das time rate of flow of charge. Mathematisch kann es dargestellt werden als

$$I = \frac{dQ}{dt}$$

Ersatz $Q = CV$ in der obigen Gleichung.

$$I = \frac{d(CV)}{dt}$$

$$\Rightarrow I = C \frac{dV}{dt}$$

$$\Rightarrow V = \frac{1}{C} \int I dt$$

Aus den obigen Gleichungen können wir schließen, dass es eine gibt linear relationship zwischen der Spannung am Kondensator und dem durch ihn fließenden Strom.

Wir wissen das power in einem elektrischen Schaltungselement kann dargestellt werden als

$$P = VI$$

Ersatz $I = C \frac{dV}{dt}$ in der obigen Gleichung.

$$P = V \lgroup C \frac{dV}{dt} \rgroup$$

$$\Rightarrow P = CV \frac{dV}{dt}$$

Durch Integration der obigen Gleichung erhalten wir die energy im Kondensator gespeichert als

$$W = \frac{1}{2}CV^2$$

Der Kondensator speichert also die Energie in Form eines elektrischen Feldes.

Netzwerkelemente können eines von beiden sein active oder passiveArt. Jeder Stromkreis oder jedes Netzwerk enthält einen dieser beiden Arten von Netzwerkelementen oder eine Kombination aus beiden.

Lassen Sie uns nun über die folgenden zwei Gesetze diskutieren, die im Volksmund als bekannt sind Kirchhoff’s laws.

• Kirchhoffs aktuelles Gesetz
• Kirchhoffs Spannungsgesetz

Kirchhoffs aktuelles Gesetz

Kirchhoffs aktuelles Gesetz (KCL) besagt, dass die algebraische Summe der Ströme, die einen Knoten verlassen (oder in diesen eintreten), gleich Null ist.

EIN Nodeist ein Punkt, an dem zwei oder mehr Schaltungselemente damit verbunden sind. Wenn nur zwei Schaltungselemente mit einem Knoten verbunden sind, spricht man von einem einfachen Knoten. Wenn drei oder mehr Schaltungselemente mit einem Knoten verbunden sind, spricht man von einem KnotenPrincipal Node.

Mathematically, KCL kann dargestellt werden als

$$\displaystyle\sum\limits_{m=1}^M I_m = 0$$

Wo,

• I_mist der m- ^te Zweigstrom, der den Knoten verlässt.

• M ist die Anzahl der Zweige, die mit einem Knoten verbunden sind.

Die obige Aussage von KCLkann auch ausgedrückt werden als "die algebraische Summe von Strömen, die in einen Knoten eintreten, ist gleich der algebraischen Summe von Strömen, die einen Knoten verlassen". Lassen Sie uns diese Aussage anhand des folgenden Beispiels überprüfen.

Beispiel

Schreiben KCL equation am Knoten P der folgenden Abbildung.

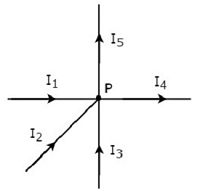
• In der obigen Abbildung, die Zweigströme I ₁ , I ₂ und I ₃ sindentering Betrachten Sie also negative Vorzeichen für diese drei Ströme.

• In der obigen Abbildung, die Zweigströme I ₄ und I ₅ sindleaving Betrachten Sie also positive Vorzeichen für diese beiden Ströme.

Das KCL equation am Knoten P wird sein

$$- I_1 - I_2 - I_3 + I_4 + I_5 = 0$$

$$\Rightarrow I_1 + I_2 + I_3 = I_4 + I_5$$

In der obigen Gleichung repräsentiert die linke Seite die Summe der eintretenden Ströme, während die rechte Seite die Summe der austretenden Ströme darstellt.

In diesem Tutorial betrachten wir das positive Vorzeichen, wenn der Strom einen Knoten verlässt, und das negative Vorzeichen, wenn er in einen Knoten eintritt. Ebenso können Sie ein negatives Vorzeichen berücksichtigen, wenn der Strom einen Knoten verlässt, und ein positives Vorzeichen, wenn er in einen Knoten eintritt. In beiden Fällen ist dieresult will be same.

Note - KCL ist unabhängig von der Art der Netzwerkelemente, die mit einem Knoten verbunden sind.

Kirchhoffs Spannungsgesetz

Das Kirchhoffsche Spannungsgesetz (KVL) besagt, dass die algebraische Summe der Spannungen um eine Schleife oder ein Netz gleich Null ist.

EIN Loopist ein Pfad, der an demselben Knoten endet, von dem aus er gestartet wurde. Im Gegensatz dazu aMesh ist eine Schleife, die keine anderen Schleifen enthält.

Mathematisch kann KVL als dargestellt werden

$$\displaystyle\sum\limits_{n=1}^N V_n = 0$$

Wo,

• V_nist die Spannung des n- ^ten Elements in einer Schleife (Masche).

• N ist die Anzahl der Netzwerkelemente in der Schleife (Netz).

Die obige Aussage von KVLkann auch ausgedrückt werden als "die algebraische Summe der Spannungsquellen ist gleich der algebraischen Summe der Spannungsabfälle, die in einer Schleife vorhanden sind." Lassen Sie uns diese Aussage anhand des folgenden Beispiels überprüfen.

Beispiel

Schreiben KVL equation um die Schleife der folgenden Schaltung.

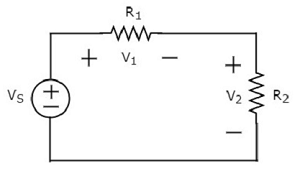
Das obige Schaltbild besteht aus einer Spannungsquelle V _S in Reihe mit zwei Widerständen R ₁ und R ₂ . Die Spannungsabfälle an den Widerständen R ₁ und R ₂ betragen V ₁ bzw. V ₂ .

Anwenden KVL um die Schleife.

$$V_S - V_1 - V_2 = 0$$

$$\Rightarrow V_S = V_1 + V_2$$

In der obigen Gleichung repräsentiert der Term auf der linken Seite eine einzelne Spannungsquelle VS. Während die rechte Seite die darstelltsum of voltage drops. In diesem Beispiel haben wir nur eine Spannungsquelle betrachtet. Deshalb enthält die linke Seite nur einen Begriff. Wenn wir mehrere Spannungsquellen betrachten, enthält die linke Seite die Summe der Spannungsquellen.

In diesem Tutorial betrachten wir das Vorzeichen der Spannung jedes Elements als die Polarität des zweiten Anschlusses, der während der Fahrt um die Schleife vorhanden ist. In ähnlicher Weise können Sie das Vorzeichen jeder Spannung als die Polarität des ersten Anschlusses betrachten, der vorhanden ist, während Sie sich um die Schleife bewegen. In beiden Fällen ist dieresult will be same.

Note - KVL ist unabhängig von der Art der Netzwerkelemente, die in einer Schleife vorhanden sind.

Lassen Sie uns in diesem Kapitel die folgenden zwei Teilungsprinzipien elektrischer Größen diskutieren.

• Aktuelles Teilungsprinzip
• Prinzip der Spannungsteilung

Aktuelles Teilungsprinzip

Wenn zwei oder mehr passive Elemente parallel geschaltet sind, wird die Strommenge, die durch jedes Element fließt, erhalten divided (gemeinsam) untereinander aus dem Strom, der in den Knoten eintritt.

Folgendes berücksichtigen circuit diagram.

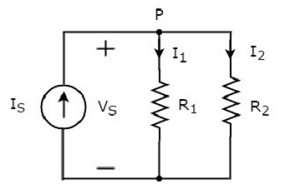
Das obige Schaltbild besteht aus einer Eingangsstromquelle I_S parallel zu zwei Widerständen R₁ und R₂. Die Spannung an jedem Element beträgtV_S. Die durch die Widerstände fließenden StrömeR₁ und R₂ sind I₁ und I₂ beziehungsweise.

Das KCL equation am Knoten P wird sein

$$I_S = I_1 + I_2$$

• Ersatz $I_1 = \frac{V_S}{R_1}$ und $I_2 = \frac{V_S}{R_2}$ in der obigen Gleichung.

$$I_S = \frac{V_S}{R_1} + \frac{V_S}{R_2} = V_S \lgroup \frac {R_2 + R_1 }{R_1 R_2} \rgroup$$

$$\Rightarrow V_S = I_S \lgroup \frac{R_1R_2}{R_1 + R_2} \rgroup$$

• Ersetzen Sie den Wert von V _S in$I_1 = \frac{V_S}{R_1}$.

$$I_1 = \frac{I_S}{R_1}\lgroup \frac{R_1 R_2}{R_1 + R_2} \rgroup$$

$$\Rightarrow I_1 = I_S\lgroup \frac{R_2}{R_1 + R_2} \rgroup$$

• Ersetzen Sie den Wert von V _S in$I_2 = \frac{V_S}{R_2}$.

$$I_2 = \frac{I_S}{R_2} \lgroup \frac{R_1 R_2}{R_1 + R_2} \rgroup$$

$$\Rightarrow I_2 = I_S \lgroup \frac{R_1}{R_1 + R_2} \rgroup$$

Aus den Gleichungen von I ₁ und I ₂ können wir verallgemeinern, dass der durch jedes passive Element fließende Strom unter Verwendung der folgenden Formel ermittelt werden kann.

$$I_N = I_S \lgroup \frac{Z_1\rVert Z_2 \rVert...\rVert Z_{N-1}}{Z_1 + Z_2 + ... + Z_N}\rgroup$$

Dies ist bekannt als current division principle und es ist anwendbar, wenn zwei oder mehr passive Elemente parallel geschaltet sind und nur ein Strom in den Knoten eintritt.

Wo,

• I _N ist der Strom, der durch das passive Element des N- ^ten Zweigs fließt .

• I _S ist der Eingangsstrom, der in den Knoten eintritt.

• Z ₁ , Z ₂ , ..., Z _N sind die Impedanzen von 1 ^st Zweig, 2 ^nd Zweig, ..., N - ^ten Zweig verbunden.

Prinzip der Spannungsteilung

Wenn zwei oder mehr passive Elemente in Reihe geschaltet sind, wird die an jedem Element vorhandene Spannungsmenge ermittelt divided (geteilt) untereinander aus der Spannung, die über diese gesamte Kombination verfügbar ist.

Folgendes berücksichtigen circuit diagram.

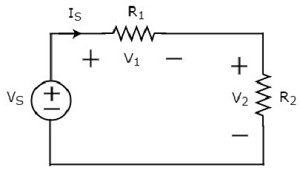
Das obige Schaltbild besteht aus einer Spannungsquelle V _S in Reihe mit zwei Widerständen R ₁ und R ₂ . Der Strom fließt durch diese Elemente ist I _S . Die Spannungsabfälle an den Widerständen R ₁ und R ₂ betragen V ₁ bzw. V ₂ .

Das KVL equation um die Schleife wird sein

$$V_S = V_1 + V_2$$

• Ersetzen Sie V ₁ = I _S R ₁ und V ₂ = I _S R ₂ in der obigen Gleichung

$$V_S = I_S R_1 + I_S R_2 = I_S(R_1 + R_2)$$

$$I_S = \frac{V_S}{R_1 + R_2}$$

• Ersetzen Sie den Wert von I _S durch V ₁ = I _S R ₁ .

$$V_1 = \lgroup \frac {V_S}{R_1 + R_2} \rgroup R_1$$

$$\Rightarrow V_1 = V_S \lgroup \frac {R_1}{R_1 + R_2} \rgroup$$

• Ersetzen Sie den Wert von I _S durch V ₂ = I _S R ₂ .

$$V_2 = \lgroup \frac {V_S}{R_1 + R_2} \rgroup R_2$$

$$\Rightarrow V_2 = V_S \lgroup \frac {R_2}{R_1 + R_2} \rgroup$$

Aus den Gleichungen von V ₁ und V ₂ können wir verallgemeinern, dass die Spannung an jedem passiven Element unter Verwendung der folgenden Formel ermittelt werden kann.

$$V_N = V_S \lgroup \frac {Z_N}{Z_1 + Z_2 +....+ Z_N}\rgroup$$

Dies ist bekannt als voltage division principle und es ist anwendbar, wenn zwei oder mehr passive Elemente in Reihe geschaltet sind und nur eine Spannung über die gesamte Kombination verfügbar ist.

Wo,

• V _N ist die Spannung am N- ^ten passiven Element.

• V _S ist die Eingangsspannung, die über die gesamte Kombination von passiven Serienelementen anliegt.

• Z ₁ , Z ₂ , ..., Z ₃ sind die Impedanzen von 1 ^st passivem Elemente, 2 ^nd passiven Element, ..., N - ^ten passiven Element verbunden.

Es gibt zwei grundlegende Methoden, die zum Lösen eines elektrischen Netzwerks verwendet werden: Nodal analysis und Mesh analysis. Lassen Sie uns in diesem Kapitel über dieNodal analysis Methode.

In der Knotenanalyse werden wir die Knotenspannungen in Bezug auf Masse berücksichtigen. Daher wird die Knotenanalyse auch als bezeichnetNode-voltage method.

Verfahren der Knotenanalyse

Befolgen Sie diese Schritte, während Sie ein elektrisches Netzwerk oder einen Stromkreis mithilfe der Knotenanalyse lösen.

• Step 1 - Identifizieren Sie die principal nodes und wählen Sie eine davon als reference node. Wir werden diesen Referenzknoten als Grund behandeln.

• Step 2 - Beschriften Sie die node voltages in Bezug auf Masse von allen Hauptknoten mit Ausnahme des Referenzknotens.

• Step 3 - Schreiben nodal equationsan allen Hauptknoten außer dem Referenzknoten. Die Knotengleichung wird erhalten, indem zuerst KCL und dann das Ohmsche Gesetz angewendet werden.

• Step 4 - Lösen Sie die in Schritt 3 erhaltenen Knotengleichungen, um die Knotenspannungen zu erhalten.

Jetzt können wir den durch jedes Element fließenden Strom und die Spannung über jedem Element, das in dem gegebenen Netzwerk vorhanden ist, unter Verwendung von Knotenspannungen finden.

Beispiel

Finden Sie den Strom, der durch den 20 Ω-Widerstand der folgenden Schaltung fließt, mit Nodal analysis.

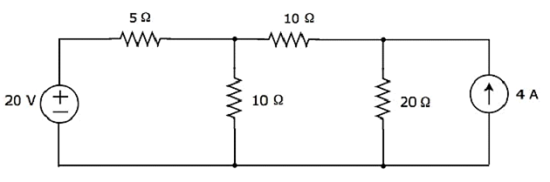
Step 1 - Es gibt three principle nodesin der obigen Schaltung. Diese sind in der folgenden Abbildung mit 1, 2 und 3 gekennzeichnet.

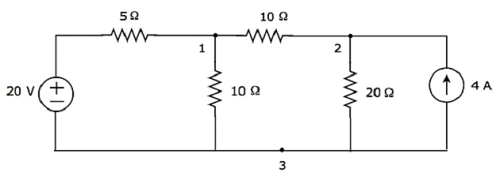
Betrachten Sie in der obigen Abbildung node 3 als Referenzknoten (Masse).

Step 2- Die Knotenspannungen V ₁ und V ₂ sind in der folgenden Abbildung gekennzeichnet.

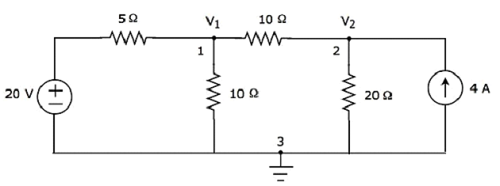
In der obigen Figur ist V ₁ die Spannung von Knoten 1 in Bezug auf Masse und V ₂ ist die Spannung von Knoten 2 in Bezug auf Masse.

Step 3 - In diesem Fall werden wir bekommen two nodal equations, da es außer Masse zwei Hauptknoten gibt, 1 und 2. Wenn wir die Knotengleichungen an einem Knoten schreiben, nehmen wir an, dass alle Ströme von dem Knoten ausgehen, für den die Stromrichtung nicht erwähnt wird, und dass die Spannung dieses Knotens größer ist als die anderer Knotenspannungen in der Schaltung.

Das nodal equation am Knoten 1 ist

$$\frac{V_1 - 20}{5} + \frac{V_1}{10} + \frac{V_1 - V_2}{10} = 0$$

$$\Rightarrow \frac{2 V_1 - 40 + V_1 + V_1 - V_2}{10} = 0$$

$$\Rightarrow 4V_1 - 40 - V_2 = 0$$

$\Rightarrow V_2 = 4V_1 - 40$ Equation 1

Das nodal equation am Knoten 2 ist

$$-4 + \frac{V_2}{20} + \frac{V_2 - V_1}{10} = 0$$

$$\Rightarrow \frac{-80 + V_2 + 2V_2 - 2V_2}{20} = 0$$

$\Rightarrow 3V_2 − 2V_1 = 80$ Equation 2

Step 4- Finden der Knotenspannungen V ₁ und V ₂ durch Lösen von Gleichung 1 und Gleichung 2.

Ersetzen Sie Gleichung 1 in Gleichung 2.

$$3(4 V_1 - 40) - 2 V_1 = 80$$

$$\Rightarrow 12 V_1 - 120 - 2V_1 =80$$

$$\Rightarrow 10 V_1 = 200$$

$$\Rightarrow V_1 = 20V$$

Ersetzen Sie V ₁ = 20 V in Gleichung 1.

$$V_2 = 4(20) - 40$$

$$\Rightarrow V_2 = 40V$$

Wir haben also die Knotenspannungen V ₁ und V ₂ als20 V und 40 V beziehungsweise.

Step 5- Die Spannung am 20 Ω-Widerstand ist nichts anderes als die Knotenspannung V ₂ und beträgt 40 V. Jetzt können wir den durch den 20 Ω-Widerstand fließenden Strom unter Verwendung des Ohmschen Gesetzes ermitteln.

$$I_{20 \Omega} = \frac{V_2}{R}$$

Ersetzen Sie die Werte von V ₂ und R in der obigen Gleichung.

$$I_{20 \Omega} = \frac{40}{20}$$

$$\Rightarrow I_{20 \Omega} = 2A$$

Daher beträgt der Strom, der durch den 20 Ω-Widerstand einer gegebenen Schaltung fließt 2 A.

Note- Aus dem obigen Beispiel können wir schließen, dass wir 'n' Knotengleichungen lösen müssen, wenn der Stromkreis 'n' Hauptknoten hat (außer dem Referenzknoten). Daher können wir die Knotenanalyse wählen, wenn dienumber of principal nodes (außer Referenzknoten) ist kleiner als die Anzahl der Maschen eines Stromkreises.

Bei der Netzanalyse werden die Ströme berücksichtigt, die durch jedes Netz fließen. Daher wird die Netzanalyse auch als bezeichnetMesh-current method.

EIN branchist ein Pfad, der zwei Knoten verbindet und ein Schaltungselement enthält. Wenn ein Zweig nur zu einem Netz gehört, entspricht der Verzweigungsstrom dem Netzstrom.

Wenn ein Zweig zwei Maschen gemeinsam ist, ist der Zweigstrom gleich der Summe (oder Differenz) zweier Maschenströme, wenn sie in derselben (oder entgegengesetzter) Richtung liegen.

Verfahren der Netzanalyse

Befolgen Sie diese Schritte, während Sie ein elektrisches Netzwerk oder einen Stromkreis mithilfe der Netzanalyse lösen.

• Step 1 - Identifizieren Sie die meshes und beschriften Sie die Maschenströme entweder im oder gegen den Uhrzeigersinn.

• Step 2 - Beobachten Sie die Strommenge, die durch jedes Element fließt, in Form von Maschenströmen.

• Step 3 - Schreiben mesh equationszu allen Maschen. Die Maschengleichung wird erhalten, indem zuerst KVL und dann das Ohmsche Gesetz angewendet werden.

• Step 4 - Lösen Sie die in Schritt 3 erhaltenen Netzgleichungen, um die zu erhalten mesh currents.

Jetzt können wir den Strom, der durch jedes Element fließt, und die Spannung über jedem Element, das in dem gegebenen Netzwerk vorhanden ist, unter Verwendung von Maschenströmen finden.

Beispiel

Ermitteln Sie die Spannung am 30 Ω-Widerstand mit Mesh analysis.

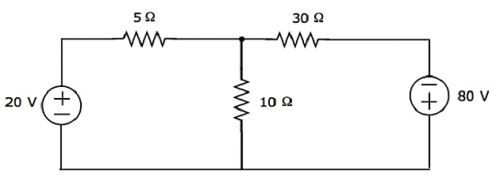
Step 1- In der obigen Schaltung befinden sich zwei Maschen. Dasmesh currentsI ₁ und I ₂ werden im Uhrzeigersinn betrachtet. Diese Maschenströme sind in der folgenden Abbildung dargestellt.

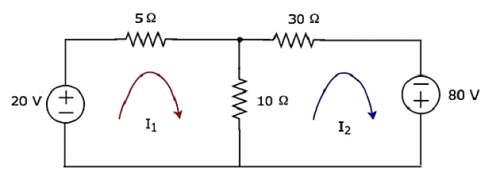
Step 2- Der Maschenstrom I ₁ fließt durch eine 20-V-Spannungsquelle und einen 5-Ω-Widerstand. In ähnlicher Weise fließt der Maschenstrom I ₂ durch einen 30 Ω-Widerstand und eine Spannungsquelle von -80 V. Die Differenz zweier Maschenströme I ₁ und I ₂ fließt jedoch durch einen 10 Ω-Widerstand, da dies der gemeinsame Zweig zweier Maschen ist.

Step 3 - In diesem Fall werden wir bekommen two mesh equationsda es zwei Maschen in der gegebenen Schaltung gibt. Wenn wir die Netzgleichungen schreiben, nehmen wir an, dass der Netzstrom dieses bestimmten Netzes größer ist als alle anderen Netzströme der Schaltung.

Das mesh equation des ersten Netzes ist

$$20 - 5I_1 -10(I_1 - I_2) = 0$$

$$\Rightarrow 20 - 15I_1 + 10I_2 = 0$$

$$\Rightarrow 10I_2 = 15I_1 - 20$$

Teilen Sie die obige Gleichung mit 5.

$$2I_2 = 3I_1 - 4$$

Multiplizieren Sie die obige Gleichung mit 2.

$4I_2 = 6I_1 - 8$ Equation 1

Das mesh equation des zweiten Netzes ist

$$-10(I_2 - I_1) - 30I_2 + 80 = 0$$

Teilen Sie die obige Gleichung mit 10.

$$-(I_2 - I_1) - 3I_2 + 8 = 0$$

$$\Rightarrow -4I_2 + I_1 + 8 = 0$$

$4I_2 = I_1 + 8$ Equation 2

Step 4- Finden der Maschenströme I ₁ und I ₂ durch Lösen von Gleichung 1 und Gleichung 2.

The left-hand side terms of Equation 1 and Equation 2 are the same. Hence, equate the right-hand side terms of Equation 1 and Equation 2 in order find the value of I₁.

$$6I_1 - 8 = I_1 + 8$$

$$\Rightarrow 5I_1 = 16$$

$$\Rightarrow I_1 = \frac{16}{5} A$$

Substitute I₁ value in Equation 2.

$$4I_2 = \frac{16}{5} + 8$$

$$\Rightarrow 4I_2 = \frac{56}{5}$$

$$\Rightarrow I_2 = \frac{14}{5} A$$

So, we got the mesh currents I₁ and I₂ as $\mathbf{\frac{16}{5}}$ A and $\mathbf{\frac{14}{5}}$ A respectively.

Step 5 − The current flowing through 30 Ω resistor is nothing but the mesh current I₂ and it is equal to $\frac{14}{5}$ A. Now, we can find the voltage across 30 Ω resistor by using Ohm’s law.

$$V_{30 \Omega} = I_2 R$$

Substitute the values of I₂ and R in the above equation.

$$V_{30 \Omega} = \lgroup \frac{14}{5} \rgroup 30$$

$$\Rightarrow V_{30 \Omega} = 84V$$

Therefore, the voltage across 30 Ω resistor of the given circuit is 84 V.

Note 1 − From the above example, we can conclude that we have to solve ‘m’ mesh equations, if the electric circuit is having ‘m’ meshes. That’s why we can choose Mesh analysis when the number of meshes is less than the number of principal nodes (except the reference node) of any electrical circuit.

Note 2 − We can choose either Nodal analysis or Mesh analysis, when the number of meshes is equal to the number of principal nodes (except the reference node) in any electric circuit.

If a circuit consists of two or more similar passive elements and are connected in exclusively of series type or parallel type, then we can replace them with a single equivalent passive element. Hence, this circuit is called as an equivalent circuit.

In this chapter, let us discuss about the following two equivalent circuits.

• Series Equivalent Circuit
• Parallel Equivalent Circuit

Series Equivalent Circuit

If similar passive elements are connected in series, then the same current will flow through all these elements. But, the voltage gets divided across each element.

Consider the following circuit diagram.

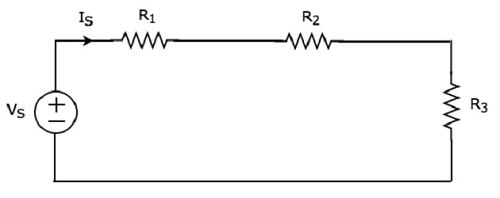
It has a single voltage source (V_S) and three resistors having resistances of R₁, R₂ and R₃. All these elements are connected in series. The current IS flows through all these elements.

The above circuit has only one mesh. The KVL equation around this mesh is

$$V_S = V_1 + V_2 + V_3$$

Substitute $V_1 = I_S R_1, \: V_2 = I_S R_2$ and $V_3 = I_S R_3$ in the above equation.

$$V_S = I_S R_1 + I_S R_2 + I_S R_3$$

$$\Rightarrow V_S = I_S(R_1 + R_2 + R_3)$$

The above equation is in the form of $V_S = I_S R_{Eq}$ where,

$$R_{Eq} = R_1 + R_2 + R_3$$

The equivalent circuit diagram of the given circuit is shown in the following figure.

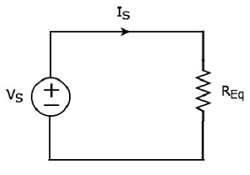
That means, if multiple resistors are connected in series, then we can replace them with an equivalent resistor. The resistance of this equivalent resistor is equal to sum of the resistances of all those multiple resistors.

Note 1 − If ‘N’ inductors having inductances of L₁, L₂, ..., L_N are connected in series, then the equivalent inductance will be

$$L_{Eq} = L_1 + L_2 + ... + L_N$$

Note 2 − If ‘N’ capacitors having capacitances of C₁, C₂, ..., C_N are connected in series, then the equivalent capacitance will be

$$\frac{1}{C_{Eq}} = \frac{1}{C_1} + \frac{1}{C_2} + ... + \frac{1}{C_N}$$

Parallel Equivalent Circuit

If similar passive elements are connected in parallel, then the same voltage will be maintained across each element. But, the current flowing through each element gets divided.

Consider the following circuit diagram.

It has a single current source (I_S) and three resistors having resistances of R₁, R₂, and R₃. All these elements are connected in parallel. The voltage (V_S) is available across all these elements.

The above circuit has only one principal node (P) except the Ground node. The KCL equation at this principal node (P) is

$$I_S = I_1 + I_2 + I_3$$

Substitute $I_1 = \frac{V_S}{R_1}, \: I_2 = \frac{V_S}{R_2}$ and $I_3 = \frac{V_S}{R_3}$ in the above equation.

$$I_S = \frac{V_S}{R_1} + \frac{V_S}{R_2} + \frac{V_S}{R_3}$$

$$\Rightarrow I_S = V_S \lgroup \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \rgroup$$

$$\Rightarrow V_S = I_S\left [ \frac{1}{\lgroup \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \rgroup} \right ]$$

The above equation is in the form of V_S = I_SR_Eq where,

$$R_{Eq} = \frac{1}{\lgroup \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \rgroup}$$

$$\frac{1}{R_{Eq}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}$$

The equivalent circuit diagram of the given circuit is shown in the following figure.

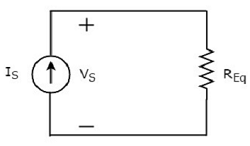
That means, if multiple resistors are connected in parallel, then we can replace them with an equivalent resistor. The resistance of this equivalent resistor is equal to the reciprocal of sum of reciprocal of each resistance of all those multiple resistors.

Note 1 − If ‘N’ inductors having inductances of L₁, L₂, ..., L_N are connected in parallel, then the equivalent inductance will be

$$\frac{1}{L_{Eq}} = \frac{1}{L_1} + \frac{1}{L_2} + ... + \frac{1}{L_N}$$

Note 2 − If ‘N’ capacitors having capacitances of C₁, C₂, ..., C_N are connected in parallel, then the equivalent capacitance will be

$$C_{Eq} = C_1 + C_2 + ... + C_N$$

In the previous chapter, we discussed about the equivalent circuits of series combination and parallel combination individually. In this chapter, let us solve an example problem by considering both series and parallel combinations of similar passive elements.

Example

Let us find the equivalent resistance across the terminals A & B of the following electrical network.

We will get the equivalent resistance across terminals A & B by minimizing the above network into a single resistor between those two terminals. For this, we have to identify the combination of resistors that are connected in series form and parallel form and then find the equivalent resistance of the respective form in every step.

The given electrical network is modified into the following form as shown in the following figure.

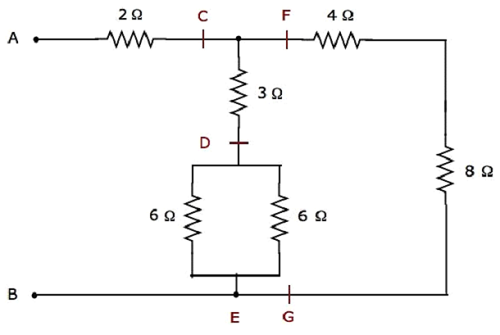
In the above figure, the letters, C to G, are used for labelling various terminals.

Step 1 − In the above network, two 6 Ω resistors are connected in parallel. So, the equivalent resistance between D & E will be 3 Ω. This can be obtained by doing the following simplification.

$$R_{DE} = \frac{6 \times 6}{6 + 6} = \frac{36}{12} = 3 \Omega$$

In the above network, the resistors 4 Ω and 8 Ω are connected in series. So, the equivalent resistance between F & G will be 12 Ω. This can be obtained by doing the following simplification.

$$R_{FG} = 4 + 8 = 12 \Omega$$

Step 2 − The simplified electrical network after Step 1 is shown in the following figure.

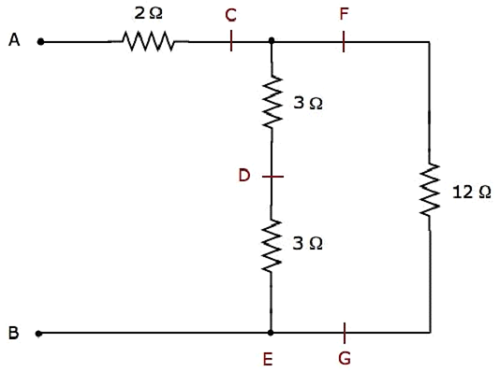
In the above network, two 3 Ω resistors are connected in series. So, the equivalent resistance between C & E will be 6 Ω. This can be obtained by doing the following simplification.

$$R_{CE} = 3 + 3 = 6 \Omega$$

Step 3 − The simplified electrical network after Step 2 is shown in the following figure.

In the above network, the resistors 6 Ω and 12 Ω are connected in parallel. So, the equivalent resistance between C & B will be 4 Ω. This can be obtained by doing the following simplification.

$$R_{CB} = \frac{6 \times 12}{6 + 12} = \frac{72}{18} = 4 \Omega$$

Step 4 − The simplified electrical network after Step 3 is shown in the following figure.

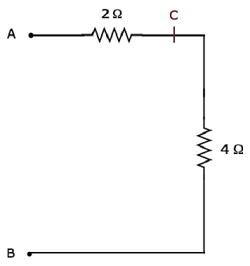
In the above network, the resistors 2 Ω and 4 Ω are connected in series between the terminals A & B. So, the equivalent resistance between A & B will be 6 Ω. This can be obtained by doing the following simplification.

$$R_{AB} = 2 + 4 = 6 \Omega$$

Therefore, the equivalent resistance between terminals A & B of the given electrical network is 6 Ω.

In the previous chapter, we discussed an example problem related equivalent resistance. There, we calculated the equivalent resistance between the terminals A & B of the given electrical network easily. Because, in every step, we got the combination of resistors that are connected in either series form or parallel form.

However, in some situations, it is difficult to simplify the network by following the previous approach. For example, the resistors connected in either delta (δ) form or star form. In such situations, we have to convert the network of one form to the other in order to simplify it further by using series combination or parallel combination. In this chapter, let us discuss about the Delta to Star Conversion.

Delta Network

Consider the following delta network as shown in the following figure.

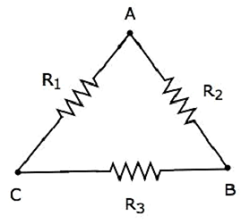
The following equations represent the equivalent resistance between two terminals of delta network, when the third terminal is kept open.

$$R_{AB} = \frac{(R_1 + R_3)R_2}{R_1 + R_2 + R_3}$$

$$R_{BC} = \frac{(R_1 + R_2)R_3}{R_1 + R_2 + R_3}$$

$$R_{CA} = \frac{(R_2 + R_3)R_1}{R_1 + R_2 + R_3}$$

Star Network

Die folgende Abbildung zeigt die equivalent star network entsprechend dem obigen Delta-Netzwerk.

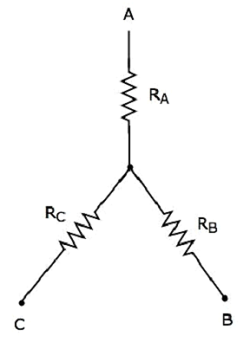
Die folgenden Gleichungen repräsentieren die equivalent resistance zwischen zwei Terminals des Sternnetzwerks, wenn das dritte Terminal offen gehalten wird.

$$R_{AB} = R_A + R_B$$

$$R_{BC} = R_B + R_C$$

$$R_{CA} = R_C + R_A$$

Star Network Resistances in Bezug auf Delta Network Resistances

Wir erhalten die folgenden Gleichungen, indem wir die Terme auf der rechten Seite der obigen Gleichungen gleichsetzen, für die die Terme auf der linken Seite gleich sind.

$R_A + R_B = \frac{(R_1 + R_3)R_2}{R_1 + R_2 + R_3}$ Equation 1

$R_B + R_C = \frac{(R_1 + R_2)R_3}{R_1 + R_2 + R_3}$ Equation 2

$R_C + R_A = \frac{(R_2 + R_3)R_1}{R_1 + R_2 + R_3}$ Equation 3

Durch Hinzufügen der obigen drei Gleichungen erhalten wir

$$2(R_A + R_B + R_C) = \frac{2(R_1 R_2 + R_2 R_3 + R_3 R_1)}{R_1 + R_2 + R_3}$$

$\Rightarrow R_A + R_B + R_C = \frac{R_1 R_2 + R_2 R_3 + R_3 R_1}{R_1 + R_2 + R_3}$ Equation 4

Subtrahieren Sie Gleichung 2 von Gleichung 4.

$R_A + R_B + R_C - (R_B + R_C) = \frac{R_1 R_2 + R_2 R_3 + R_3 R_1}{R_1 + R_2 + R_3} - \frac{(R_1 + R_2)R_3}{R_1 + R_2 + R_3}$

$$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$$

Durch Subtrahieren von Gleichung 3 von Gleichung 4 erhalten wir

$$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$$

Durch Subtrahieren von Gleichung 1 von Gleichung 4 erhalten wir

$$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$$

Unter Verwendung der obigen Beziehungen können wir die Widerstände des Sternnetzwerks aus den Widerständen des Delta-Netzwerks ermitteln. Auf diese Weise können wir a konvertierendelta network in ein star network.

Beispiel

Berechnen wir die resistances of star network, die dem Delta-Netzwerk entsprechen, wie in der folgenden Abbildung gezeigt.

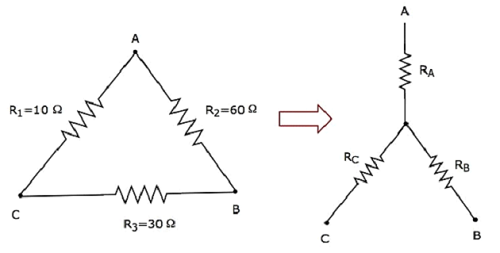
Angenommen resistances of delta networkals R ₁ = 10 Ω, R ₂ = 60 Ω und R ₃ = 30 Ω.

Wir kennen die folgenden Beziehungen der Widerstände des Sternnetzwerks in Bezug auf die Widerstände des Delta-Netzwerks.

$$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$$

$$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$$

$$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$$

Ersetzen Sie die Werte von R ₁ , R ₂ und R ₃ durch die obigen Gleichungen.

$$R_A = \frac{10 \times 60}{10 +60+30} = \frac{600}{100} = 6\Omega$$

$$R_B = \frac{60 \times 30}{10 +60+30} = \frac{1800}{100} = 18\Omega$$

$$R_C = \frac{30 \times 10}{10 +60+30} = \frac{300}{100} = 3\Omega$$

Also haben wir die Widerstände des Sternennetzwerks als R_A = 6 Ω, R_B = 18 Ω und R_C = 3 Ω, die den Widerständen des gegebenen Delta-Netzwerks entsprechen.

Im vorherigen Kapitel haben wir die Umwandlung des Delta-Netzwerks in ein äquivalentes Sternnetzwerk erörtert. Lassen Sie uns nun über die Umwandlung des Sternnetzwerks in ein äquivalentes Delta-Netzwerk diskutieren. Diese Konvertierung wird als bezeichnetStar to Delta Conversion.

Im vorigen Kapitel haben wir die resistances of star network vom Delta-Netzwerk als

$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$ Equation 1

$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$ Equation 2

$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$ Equation 3

Delta Network Resistances in Bezug auf Star Network Resistances

Manipulieren wir die obigen Gleichungen, um die Widerstände des Delta-Netzwerks in Form der Widerstände des Sternnetzwerks zu erhalten.

• Multiply jeder Satz von zwei Gleichungen und dann add.

$$R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2^2 R_3 + R_2 R_3^2 R_1 + R_3 R_1^2 R_2}{(R_1 + R_2 + R_3)^2}$$

$$\Rightarrow R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2 R_3(R_1 + R_2 + R_3)}{(R_1 + R_2 + R_3)^2}$$

$\Rightarrow R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2 R_3}{R_1 + R_2 + R_3}$ Equation 4

• Durch Teilen von Gleichung 4 mit Gleichung 2 erhalten wir

$$\frac{R_A R_B + R_B R_C + R_C R_A}{R_B} = R_1$$

$$\Rightarrow R_1 = R_C + R_A + \frac{R_C R_A}{R_B}$$

• Durch Teilen von Gleichung 4 mit Gleichung 3 erhalten wir

$$R_2 = R_A + R_B + \frac{R_A R_B}{R_C}$$

• Durch Teilen von Gleichung 4 mit Gleichung 1 erhalten wir

$$R_3 = R_B + R_C + \frac{R_B R_C}{R_A}$$

Unter Verwendung der obigen Beziehungen können wir die Widerstände des Delta-Netzwerks aus den Widerständen des Sternnetzwerks ermitteln. Auf diese Weise können wir konvertierenstar network into delta network.

Beispiel

Berechnen wir die resistances of delta network, die dem des Sternennetzwerks entsprechen, wie in der folgenden Abbildung gezeigt.

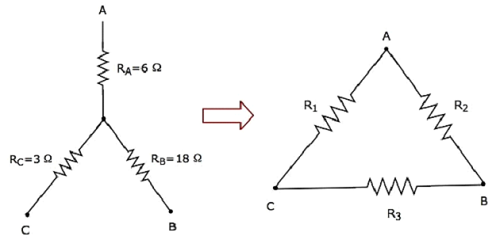
Angenommen resistances of star networkals R _A = 6 Ω, R _B = 18 Ω und R _C = 3 Ω .

Wir kennen die folgenden Beziehungen der resistances of delta network in Bezug auf die Widerstände des Sternennetzwerks.

$$R_1 = R_C + R_A + \frac{R_C R_A}{R_B}$$

$$R_2 = R_A + R_B + \frac{R_A R_B}{R_C}$$

$$R_3 = R_B + R_C + \frac{R_B R_C}{R_A}$$

Ersetzen Sie die Werte von R _A , R _B und R _C durch die obigen Gleichungen.

$$R_1 = 3 + 6 + \frac{3 \times 6}{18} = 9 + 1 = 10 \Omega$$

$$R_2 = 6 + 18 + \frac{6 \times 18}{3} = 24 + 36 = 60 \Omega$$

$$R_3 = 18 + 3 + \frac{18 \times 3}{6} = 21 + 9 = 30 \Omega$$

Also haben wir die Widerstände des Delta-Netzwerks als R₁ = 10 Ω, R₂ = 60 Ω und R₃ = 30 Ω, die den Widerständen des gegebenen Sternnetzwerks entsprechen.

Die Netzwerktopologie ist eine grafische Darstellung elektrischer Schaltkreise. Es ist nützlich, um komplexe Stromkreise zu analysieren, indem sie in Netzwerkgraphen umgewandelt werden. Die Netzwerktopologie wird auch als bezeichnetGraph theory.

Grundlegende Terminologie der Netzwerktopologie

Lassen Sie uns nun die grundlegende Terminologie dieser Netzwerktopologie diskutieren.

Graph

Netzwerkgraph wird einfach als bezeichnet graph. Es besteht aus einer Reihe von Knoten, die durch Zweige verbunden sind. In Diagrammen ist ein Knoten ein gemeinsamer Punkt aus zwei oder mehr Zweigen. Manchmal kann nur ein einziger Zweig eine Verbindung zum Knoten herstellen. Ein Zweig ist ein Liniensegment, das zwei Knoten verbindet.

Jeder Stromkreis oder jedes Netzwerk kann in ein Äquivalent umgewandelt werden graphdurch Ersetzen der passiven Elemente und Spannungsquellen durch Kurzschlüsse und der Stromquellen durch Unterbrechungen. Das heißt, die Liniensegmente in der Grafik stellen die Zweige dar, die entweder passiven Elementen oder Spannungsquellen des Stromkreises entsprechen.

Beispiel

Betrachten wir Folgendes electric circuit.

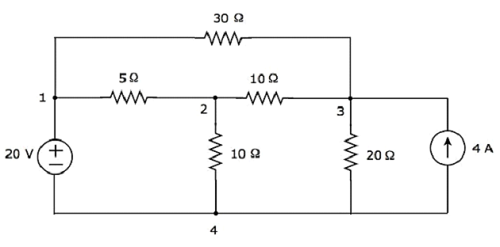
In der obigen Schaltung gibt es four principal nodes und diese sind mit 1, 2, 3 und 4 gekennzeichnet. Es gibt seven branches In der obigen Schaltung enthält ein Zweig eine 20-V-Spannungsquelle, ein anderer Zweig eine 4-A-Stromquelle und die verbleibenden fünf Zweige Widerstände mit Widerständen von 30 Ω, 5 Ω, 10 Ω, 10 Ω bzw. 20 Ω.

Ein Äquivalent graph entsprechend dem obigen Stromkreis ist in der folgenden Abbildung dargestellt.

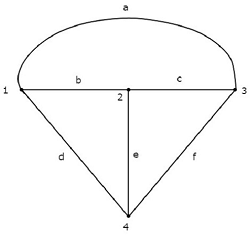
In der obigen Grafik gibt es four nodesund diese sind mit 1, 2, 3 bzw. 4 gekennzeichnet. Diese sind die gleichen wie die der Hauptknoten im Stromkreis. Es gibtsix branches in der obigen Grafik sind diese mit a, b, c, d, e und f gekennzeichnet.

In diesem Fall haben wir one branch less in der Grafik, weil die 4 A-Stromquelle als offener Stromkreis ausgeführt wird, während der Stromkreis in seine äquivalente Grafik umgewandelt wird.

Aus diesem Beispiel können wir die folgenden Punkte schließen:

• Das number of nodes Das Vorhandensein in einem Diagramm entspricht der Anzahl der in einem Stromkreis vorhandenen Hauptknoten.

• Das number of branches Das Vorhandensein in einem Diagramm ist kleiner oder gleich der Anzahl der in einem Stromkreis vorhandenen Zweige.

Arten von Graphen

Im Folgenden sind die Arten von Diagrammen aufgeführt:

• Verbundenes Diagramm
• Nicht verbundenes Diagramm
• Gerichteter Graph
• Ungerichteter Graph

Lassen Sie uns nun diese Diagramme einzeln diskutieren.

Verbundenes Diagramm

Wenn zwischen einem der beiden Knoten eines Graphen mindestens ein Zweig vorhanden ist, wird er als a bezeichnet connected graph. Das bedeutet, dass jeder Knoten im verbundenen Diagramm einen oder mehrere Zweige hat, die mit ihm verbunden sind. Daher wird kein Knoten als isoliert oder getrennt dargestellt.

Das im vorherigen Beispiel gezeigte Diagramm ist a connected graph. Hier sind alle Knoten durch drei Zweige verbunden.

Nicht verbundenes Diagramm

Wenn im Diagramm mindestens ein Knoten vorhanden ist, der nicht einmal durch einen einzelnen Zweig verbunden ist, wird er als Knoten aufgerufen unconnected graph. Es gibt also einen oder mehrere isolierte Knoten in einem nicht verbundenen Diagramm.

Betrachten Sie das in der folgenden Abbildung gezeigte Diagramm.

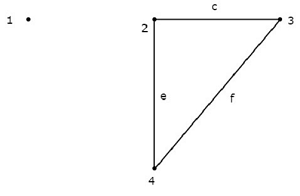
In diesem Diagramm sind die Knoten 2, 3 und 4 durch jeweils zwei Zweige verbunden. Es wurde jedoch nicht einmal ein Zweig mit dem verbundennode 1. So wird der Knoten 1 zu einemisolated node. Daher ist der obige Graph einunconnected graph.

Gerichteter Graph

Wenn alle Zweige eines Diagramms mit Pfeilen dargestellt sind, wird dieses Diagramm als a bezeichnet directed graph. Diese Pfeile geben die Richtung des Stromflusses in jedem Zweig an. Daher wird dieser Graph auch als bezeichnetoriented graph.

Betrachten Sie das in der folgenden Abbildung gezeigte Diagramm.

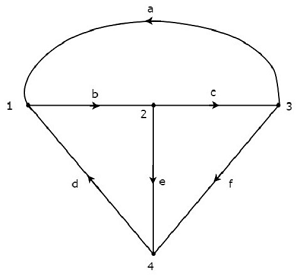
In der obigen Grafik ist die Richtung des Stromflusses in jedem Zweig mit einem Pfeil dargestellt. Daher ist es eindirected graph.

Ungerichteter Graph

Wenn die Zweige eines Diagramms nicht mit Pfeilen dargestellt werden, wird dieses Diagramm als undirected graph. Da es keine Richtungen des Stromflusses gibt, wird dieser Graph auch als bezeichnetunoriented graph.

Das Diagramm, das im ersten Beispiel dieses Kapitels gezeigt wurde, ist ein unoriented graph, weil es keine Pfeile auf den Zweigen dieses Graphen gibt.

Untergraph und seine Typen

Ein Teil des Diagramms wird als a bezeichnet subgraph. Wir erhalten Untergraphen, indem wir einige Knoten und / oder Zweige eines bestimmten Graphen entfernen. Die Anzahl der Zweige und / oder Knoten eines Untergraphen ist also geringer als die des ursprünglichen Graphen. Wir können daher schließen, dass ein Untergraph eine Teilmenge eines Graphen ist.

Es folgen die two types von Untergraphen.

• Tree
• Co-Tree

Baum

Baum ist ein zusammenhängender Untergraph eines bestimmten Diagramms, der alle Knoten eines Diagramms enthält. In diesem Untergraphen sollte sich jedoch keine Schleife befinden. Die Zweige eines Baumes heißen alstwigs.

Folgendes berücksichtigen connected subgraph des Diagramms, das im Beispiel am Anfang dieses Kapitels gezeigt wird.

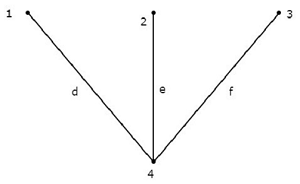
Dieser verbundene Untergraph enthält alle vier Knoten des angegebenen Graphen und es gibt keine Schleife. Daher ist es einTree.

Dieser Baum hat nur drei Zweige von sechs Zweigen eines bestimmten Graphen. Denn wenn wir nur einen Zweig der verbleibenden Zweige des Graphen betrachten, gibt es eine Schleife im oben verbundenen Teilgraphen. Dann ist der resultierende verbundene Untergraph kein Baum.

Aus dem obigen Baum können wir schließen, dass die number of branches die in einem Baum vorhanden sind, sollten gleich sein n - 1 Dabei ist 'n' die Anzahl der Knoten des angegebenen Graphen.

Co-Baum

Co-Tree ist ein Untergraph, der mit den Zweigen gebildet wird, die beim Bilden eines Baumes entfernt werden. Daher heißt es alsComplementeines Baumes. Für jeden Baum gibt es einen entsprechenden Co-Baum, dessen Zweige als bezeichnet werdenlinksoder Akkorde. Im Allgemeinen werden die Links mit gepunkteten Linien dargestellt.

Das Co-Tree Entsprechend dem obigen Baum ist in der folgenden Abbildung dargestellt.

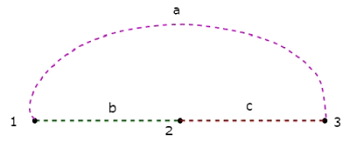
Dieser Co-Tree hat nur drei Knoten anstelle von vier Knoten des angegebenen Graphen, da Knoten 4 vom obigen Co-Tree isoliert ist. Daher muss der Co-Tree kein verbundener Untergraph sein. Dieser Co-Baum hat drei Zweige und sie bilden eine Schleife.

Das number of branchesDie in einem Co-Baum vorhandenen Werte entsprechen der Differenz zwischen der Anzahl der Zweige eines bestimmten Graphen und der Anzahl der Zweige. Mathematisch kann es geschrieben werden als

$$l = b - (n - 1)$$

$$l = b - n + 1$$

Wo,

• l ist die Anzahl der Links.
• b ist die Anzahl der in einem bestimmten Diagramm vorhandenen Zweige.
• n ist die Anzahl der in einem bestimmten Diagramm vorhandenen Knoten.

Wenn wir einen Baum und seinen entsprechenden Co-Baum kombinieren, erhalten wir den original graph Wie nachfolgend dargestellt.

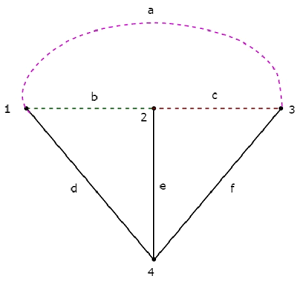
Die Äste d, e & f sind durch durchgezogene Linien dargestellt. Die Co-Tree-Zweige a, b und c sind gestrichelt dargestellt.

Im vorherigen Kapitel haben wir erläutert, wie ein Stromkreis in einen äquivalenten Graphen umgewandelt wird. Lassen Sie uns nun die Netzwerktopologiematrizen diskutieren, die zur Lösung von Stromkreisen oder Netzwerkproblemen mithilfe ihrer entsprechenden Diagramme nützlich sind.

Mit Netzwerkgraphen verknüpfte Matrizen

Es folgen die drei Matrizen, die in der Graphentheorie verwendet werden.

• Inzidenzmatrix
• Grundlegende Schleifenmatrix
• Fundamental Cut Set Matrix

Inzidenzmatrix

Eine Inzidenzmatrix repräsentiert den Graphen eines bestimmten Stromkreises oder Netzwerks. Daher ist es möglich, den Graphen desselben Stromkreises oder Netzwerks aus dem zu zeichnenincidence matrix.

Wir wissen, dass der Graph aus einer Reihe von Knoten besteht und diese durch einige Zweige verbunden sind. Das Verbinden von Zweigen mit einem Knoten wird daher als Inzidenz bezeichnet. Die Inzidenzmatrix wird mit dem Buchstaben A dargestellt. Sie wird auch als Knoten-zu-Verzweigungs-Inzidenzmatrix oder bezeichnetnode incidence matrix.

Wenn es 'n' Knoten gibt und 'b' Zweige in a vorhanden sind directed graphDann hat die Inzidenzmatrix 'n' Zeilen und 'b' Spalten. Hier entsprechen Zeilen und Spalten den Knoten und Zweigen eines gerichteten Graphen. Daher dieorder der Inzidenzmatrix wird sein n × b.

Das elements of incidence matrix wird einen dieser drei Werte haben, +1, -1 und 0.

• Wenn der Zweigstrom von einem ausgewählten Knoten abfließt, beträgt der Wert des Elements +1.

• Wenn der Verzweigungsstrom in Richtung eines ausgewählten Knotens fließt, ist der Wert des Elements -1.

• Wenn der Verzweigungsstrom weder an einem ausgewählten Knoten eintritt noch von einem ausgewählten Knoten austritt, ist der Wert des Elements 0.

Verfahren zum Auffinden der Inzidenzmatrix

Befolgen Sie diese Schritte, um die Inzidenzmatrix des gerichteten Graphen zu ermitteln.

• Wählen Sie einen Knoten zu einem Zeitpunkt des angegebenen gerichteten Graphen aus und füllen Sie die Werte der Elemente der Inzidenzmatrix, die diesem Knoten entsprechen, in einer Reihe aus.

• Wiederholen Sie den obigen Schritt für alle Knoten des angegebenen gerichteten Graphen.

Beispiel

Folgendes berücksichtigen directed graph.

Das incidence matrix entsprechend dem oben gerichteten Graphen wird

$$A = \begin{bmatrix}-1 & 1 & 0 & -1 & 0 & 0\\0 & -1 & 1 & 0 & 1 & 0\\1 & 0 & -1 & 0 & 0 & 1 \\0 & 0 & 0 & 1 & -1 & -1 \end{bmatrix}$$

Die Zeilen und Spalten der obigen Matrix repräsentieren die Knoten und Zweige eines gegebenen gerichteten Graphen. Die Reihenfolge dieser Inzidenzmatrix ist 4 × 6.

Durch Beobachtung der obigen Inzidenzmatrix können wir schließen, dass die summationder Spaltenelemente der Inzidenzmatrix ist gleich Null. Das heißt, ein Zweigstrom verlässt einen Knoten und tritt nur an einem anderen einzelnen Knoten ein.

Note- Wenn das angegebene Diagramm ein nicht gerichteter Typ ist, konvertieren Sie es in ein gerichtetes Diagramm, indem Sie die Pfeile auf jedem Zweig davon darstellen. Wir können die beliebige Richtung des Stromflusses in jedem Zweig berücksichtigen.

Grundlegende Schleifenmatrix

Grundschleife oder f-loopist eine Schleife, die nur einen Link und einen oder mehrere Zweige enthält. Die Anzahl der f-Schleifen entspricht also der Anzahl der Verbindungen. Die Grundschleifenmatrix wird mit dem Buchstaben B dargestellt. Sie wird auch als bezeichnetfundamental circuit matrixund Tie-Set-Matrix. Diese Matrix gibt die Beziehung zwischen Zweigströmen und Verbindungsströmen an.

Wenn es 'n' Knoten gibt und 'b' Zweige in a vorhanden sind directed graphDann ist die Anzahl der in einem Co-Baum vorhandenen Links, die dem ausgewählten Baum eines gegebenen Graphen entspricht, b-n + 1.

Die Grundschleifenmatrix hat also 'b-n + 1' Zeilen und 'b' Spalten. Hier entsprechen Zeilen und Spalten den Verknüpfungen von Co-Tree und Zweigen eines bestimmten Graphen. Daher ist die Reihenfolge der Grundschleifenmatrix(b - n + 1) × b.

Das elements of fundamental loop matrix wird einen dieser drei Werte haben, +1, -1 und 0.

• Der Wert des Elements ist +1 für die Verknüpfung der ausgewählten f-Schleife.

• Der Wert der Elemente ist 0 für die verbleibenden Links und Zweige, die nicht Teil der ausgewählten f-Schleife sind.

• Wenn die Richtung des Zweigstroms der ausgewählten f-Schleife dieselbe ist wie die des Verbindungsstroms der f-Schleife, ist der Wert des Elements +1.

• Wenn die Richtung des Zweigstroms der ausgewählten f-Schleife der Richtung des f-Schleifen-Verbindungsstroms entgegengesetzt ist, ist der Wert des Elements -1.

Vorgehensweise zum Auffinden der Fundamental Loop Matrix

Befolgen Sie diese Schritte, um die Grundschleifenmatrix eines bestimmten gerichteten Graphen zu finden.

• Wählen Sie einen Baum eines bestimmten gerichteten Graphen aus.

• Wenn Sie jeweils einen Link einfügen, erhalten Sie eine f-Schleife. Füllen Sie die Werte der Elemente, die dieser f-Schleife entsprechen, in eine Reihe der Grundschleifenmatrix.

• Wiederholen Sie den obigen Schritt für alle Links.

Beispiel

Schauen Sie sich den folgenden Baum an directed graph, die für die Inzidenzmatrix berücksichtigt wird.

Der obige Baum enthält drei Zweige d, e & f. Daher sind die Zweige a, b und c die Verknüpfungen des Co-Baums, die dem obigen Baum entsprechen. Wenn Sie jeweils einen Link zum obigen Baum einfügen, erhalten Sie einenf-loop. Es werden also drei seinf-loops, da es drei links gibt. Diese drei f-Schleifen sind in der folgenden Abbildung dargestellt.

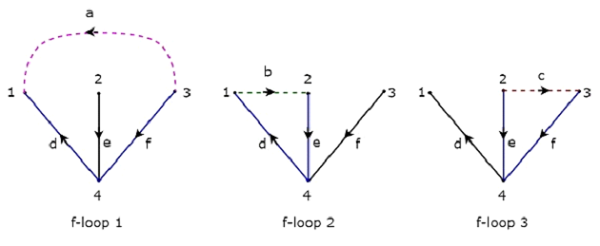
In der obigen Abbildung bilden die Zweige, die mit farbigen Linien dargestellt sind, f-Schleifen. Wir erhalten die zeilenweisen Elementwerte der Tie-Set-Matrix aus jeder f-Schleife. Also, dieTieset matrix des oben betrachteten Baumes wird sein

$$B = \begin{bmatrix}1 & 0 & 0 & -1 & 0 & -1\\0 & 1 & 0 & 1 & 1 & 0\\0 & 0 & 1 & 0 & -1 & 1 \end{bmatrix}$$

Die Zeilen und Spalten der obigen Matrix repräsentieren die Verknüpfungen und Zweige eines gegebenen gerichteten Graphen. Die Reihenfolge dieser Inzidenzmatrix ist 3 × 6.

Das number of Fundamental loop matriceseines gerichteten Graphen entspricht der Anzahl der Bäume dieses gerichteten Graphen. Weil jeder Baum eine Grundschleifenmatrix hat.

Grundlegende Cut-Set-Matrix

Grundschnitt oder f-cut setist die minimale Anzahl von Zweigen, die aus einem Diagramm so entfernt werden, dass das ursprüngliche Diagramm zu zwei isolierten Untergraphen wird. Das F-Cut-Set enthält nurone twigund einen oder mehrere Links. Die Anzahl der F-Cut-Sets entspricht also der Anzahl der Zweige.

Fundamental cut set matrix wird mit dem Buchstaben C dargestellt. Diese Matrix gibt die Beziehung zwischen Zweigspannungen und Zweigspannungen an.

Wenn es 'n' Knoten gibt und 'b' Zweige in a vorhanden sind directed graphDann ist die Anzahl der in einem ausgewählten Baum eines bestimmten Graphen vorhandenen Zweige n-1. Die grundlegende Schnittmengenmatrix hat also 'n-1' Zeilen und 'b' Spalten. Hier entsprechen Zeilen und Spalten den Zweigen des ausgewählten Baums und den Zweigen eines bestimmten Diagramms. Daher dieorder der fundamentalen Schnittmenge Matrix wird sein (n-1) × b.

Das elements of fundamental cut set matrix wird einen dieser drei Werte haben, +1, -1 und 0.

• Der Wert des Elements beträgt +1 für den Zweig des ausgewählten f-Cutset.

• Der Wert der Elemente ist 0 für die verbleibenden Zweige und Links, die nicht Teil des ausgewählten f-Cutset sind.

• Wenn die Richtung des Verbindungsstroms des ausgewählten F-Cut-Sets mit der des F-Cutset-Zweigstroms übereinstimmt, beträgt der Wert des Elements +1.

• Wenn die Richtung des Verbindungsstroms des ausgewählten f-Schnitt-Satzes der des f-Schnitt-Zweigstroms entgegengesetzt ist, ist der Wert des Elements -1.

Vorgehensweise zum Auffinden der Fundamental Cut-Set Matrix

Befolgen Sie diese Schritte, um die grundlegende Schnittmengenmatrix eines bestimmten gerichteten Graphen zu finden.

• Wählen Sie einen Baum mit einem bestimmten gerichteten Diagramm aus und stellen Sie die Verknüpfungen mit den gepunkteten Linien dar.

• Wenn Sie jeweils einen Zweig und die erforderlichen Links entfernen, erhalten Sie einen F-Cut-Satz. Füllen Sie die Werte der Elemente, die diesem F-Schnitt-Satz entsprechen, in eine Reihe grundlegender Schnitt-Satz-Matrix.

• Wiederholen Sie den obigen Schritt für alle Zweige.

Beispiel

Betrachten Sie das gleiche directed graph , die wir im Abschnitt der Inzidenzmatrix besprochen haben. Wählen Sie die Zweige d, e & f dieses gerichteten Graphen als Zweige aus. Die verbleibenden Zweige a, b und c dieses gerichteten Graphen sind also die Verknüpfungen.

Das twigs d, e & f sind mit durchgezogenen Linien und dargestellt links a, b & c sind in der folgenden Abbildung mit gepunkteten Linien dargestellt.

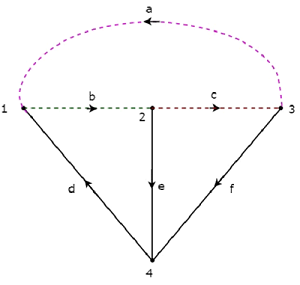
Wenn Sie jeweils einen Zweig und die erforderlichen Links entfernen, erhalten Sie einen F-Cut-Satz. Es wird also drei F-Cut-Sets geben, da es drei Zweige gibt. Diese dreif-cut sets sind in der folgenden Abbildung dargestellt.

Wir werden drei F-Cut-Sätze haben, indem wir einen Satz Zweige und Glieder von C ₁ , C ₂ und C ₃ entfernen . Wir erhalten die zeilenweisen Elementwerte der fundamentalen Schnittmengenmatrix aus jeder f-Schnittmenge. Also, diefundamental cut set matrix des oben betrachteten Baumes wird sein

$$C = \begin{bmatrix}1 & -1 & 0 & 1 & 0 & 0\\0 & -1 & 1 & 0 & 1 & 0\\1 & 0 & -1 & 0 & 0 & 1 \end{bmatrix}$$

Die Zeilen und Spalten der obigen Matrix repräsentieren die Zweige und Zweige eines gegebenen gerichteten Graphen. Die Reihenfolge dieser fundamentalen Schnittmengenmatrix ist 3 × 6.

Das number of Fundamental cut set matriceseines gerichteten Graphen entspricht der Anzahl der Bäume dieses gerichteten Graphen. Weil jeder Baum eine fundamentale Schnittmengenmatrix hat.

Superposition theorembasiert auf dem Konzept der Linearität zwischen der Reaktion und der Erregung eines Stromkreises. Es heißt, dass die Antwort in einem bestimmten Zweig einer linearen Schaltung, wenn mehrere unabhängige Quellen gleichzeitig wirken, der Summe der Antworten entspricht, die auf jede unabhängige Quelle zurückzuführen sind, die gleichzeitig wirkt.

In this method, we will consider only one independent source at a time. So, we have to eliminate the remaining independent sources from the circuit. We can eliminate the voltage sources by shorting their two terminals and similarly, the current sources by opening their two terminals.

Therefore, we need to find the response in a particular branch ‘n’ times if there are ‘n’ independent sources. The response in a particular branch could be either current flowing through that branch or voltage across that branch.

Procedure of Superposition Theorem

Follow these steps in order to find the response in a particular branch using superposition theorem.

Step 1 − Find the response in a particular branch by considering one independent source and eliminating the remaining independent sources present in the network.

Step 2 − Repeat Step 1 for all independent sources present in the network.

Step 3 − Add all the responses in order to get the overall response in a particular branch when all independent sources are present in the network.

Example

Find the current flowing through 20 Ω resistor of the following circuit using superposition theorem.

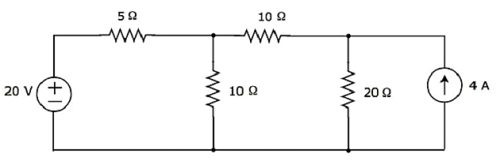
Step 1 − Let us find the current flowing through 20 Ω resistor by considering only 20 V voltage source. In this case, we can eliminate the 4 A current source by making open circuit of it. The modified circuit diagram is shown in the following figure.

There is only one principal node except Ground in the above circuit. So, we can use nodal analysis method. The node voltage V₁ is labelled in the following figure. Here, V₁ is the voltage from node 1 with respect to ground.

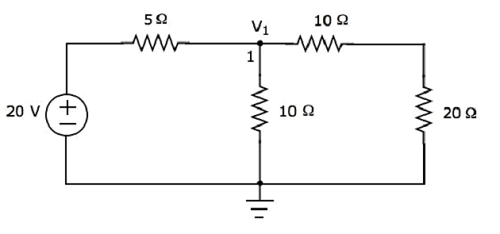
The nodal equation at node 1 is

$$\frac{V_1 - 20}{5} + \frac{V_1}{10} + \frac{V_1}{10 + 20} = 0$$

$$\Rightarrow \frac{6V_1 - 120 + 3V_1 + V_1}{30} = 0$$

$$\Rightarrow 10V_1 = 120$$

$$\Rightarrow V_1 = 12V$$

The current flowing through 20 Ω resistor can be found by doing the following simplification.

$$I_1 = \frac{V_1}{10 + 20}$$

Substitute the value of V₁ in the above equation.

$$I_1 = \frac{12}{10 + 20} = \frac{12}{30} = 0.4 A$$

Therefore, the current flowing through 20 Ω resistor is 0.4 A, when only 20 V voltage source is considered.

Step 2 − Let us find the current flowing through 20 Ω resistor by considering only 4 A current source. In this case, we can eliminate the 20 V voltage source by making short-circuit of it. The modified circuit diagram is shown in the following figure.

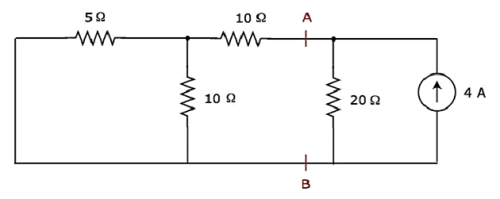
In the above circuit, there are three resistors to the left of terminals A & B. We can replace these resistors with a single equivalent resistor. Here, 5 Ω & 10 Ω resistors are connected in parallel and the entire combination is in series with 10 Ω resistor.

The equivalent resistance to the left of terminals A & B will be

$$R_{AB} = \lgroup \frac{5 \times 10}{5 + 10} \rgroup + 10 = \frac{10}{3} + 10 = \frac{40}{3} \Omega$$

The simplified circuit diagram is shown in the following figure.

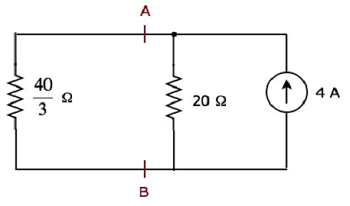
We can find the current flowing through 20 Ω resistor, by using current division principle.

$$I_2 = I_S \lgroup \frac{R_1}{R_1 + R_2} \rgroup$$

Substitute $I_S = 4A,\: R_1 = \frac{40}{3} \Omega$ and $R_2 = 20 \Omega$ in the above equation.

$$I_2 = 4 \lgroup \frac{\frac{40}{3}}{\frac{40}{3} + 20} \rgroup = 4 \lgroup \frac{40}{100} \rgroup = 1.6 A$$

Therefore, the current flowing through 20 Ω resistor is 1.6 A, when only 4 A current source is considered.

Step 3 − We will get the current flowing through 20 Ω resistor of the given circuit by doing the addition of two currents that we got in step 1 and step 2. Mathematically, it can be written as

$$I = I_1 + I_2$$

Substitute, the values of I₁ and I₂ in the above equation.

$$I = 0.4 + 1.6 = 2 A$$

Therefore, the current flowing through 20 Ω resistor of given circuit is 2 A.

Note − We can’t apply superposition theorem directly in order to find the amount of power delivered to any resistor that is present in a linear circuit, just by doing the addition of powers delivered to that resistor due to each independent source. Rather, we can calculate either total current flowing through or voltage across that resistor by using superposition theorem and from that, we can calculate the amount of power delivered to that resistor using $I^2 R$ or $\frac{V^2}{R}$.

Thevenin’s theorem states that any two terminal linear network or circuit can be represented with an equivalent network or circuit, which consists of a voltage source in series with a resistor. It is known as Thevenin’s equivalent circuit. A linear circuit may contain independent sources, dependent sources, and resistors.

If the circuit contains multiple independent sources, dependent sources, and resistors, then the response in an element can be easily found by replacing the entire network to the left of that element with a Thevenin’s equivalent circuit.

The response in an element can be the voltage across that element, current flowing through that element, or power dissipated across that element.

This concept is illustrated in following figures.

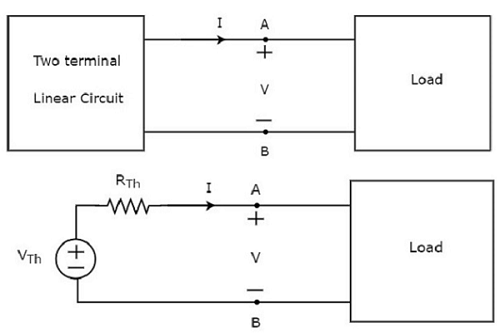
Thevenin’s equivalent circuit resembles a practical voltage source. Hence, it has a voltage source in series with a resistor.

• The voltage source present in the Thevenin’s equivalent circuit is called as Thevenin’s equivalent voltage or simply Thevenin’s voltage, V_Th.

• The resistor present in the Thevenin’s equivalent circuit is called as Thevenin’s equivalent resistor or simply Thevenin’s resistor, R_Th.

Methods of Finding Thevenin’s Equivalent Circuit

There are three methods for finding a Thevenin’s equivalent circuit. Based on the type of sources that are present in the network, we can choose one of these three methods. Now, let us discuss two methods one by one. We will discuss the third method in the next chapter.

Method 1

Follow these steps in order to find the Thevenin’s equivalent circuit, when only the sources of independent type are present.

• Step 1 − Consider the circuit diagram by opening the terminals with respect to which the Thevenin’s equivalent circuit is to be found.

• Step 2 − Find Thevenin’s voltage V_Th across the open terminals of the above circuit.

• Step 3 − Find Thevenin’s resistance R_Th across the open terminals of the above circuit by eliminating the independent sources present in it.

• Step 4 − Draw the Thevenin’s equivalent circuit by connecting a Thevenin’s voltage V_Th in series with a Thevenin’s resistance R_Th.

Now, we can find the response in an element that lies to the right side of Thevenin’s equivalent circuit.

Example

Find the current flowing through 20 Ω resistor by first finding a Thevenin’s equivalent circuit to the left of terminals A and B.

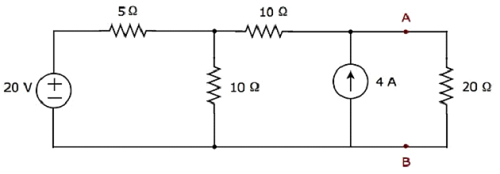
Step 1 − In order to find the Thevenin’s equivalent circuit to the left side of terminals A & B, we should remove the 20 Ω resistor from the network by opening the terminals A & B. The modified circuit diagram is shown in the following figure.

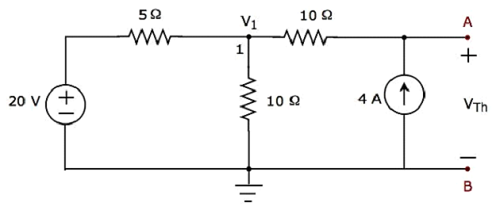
Step 2 − Calculation of Thevenin’s voltage V_Th.

There is only one principal node except Ground in the above circuit. So, we can use nodal analysis method. The node voltage V₁ and Thevenin’s voltage V_Th are labelled in the above figure. Here, V₁ is the voltage from node 1 with respect to Ground and V_Th is the voltage across 4 A current source.

• The nodal equation at node 1 is

$$\frac{V_1 - 20}{5} + \frac{V_1}{10} - 4 = 0$$

$$\Rightarrow \frac{2V_1 - 40 + V_1 - 40}{10} = 0$$

$$\Rightarrow 3V_1 - 80 = 0$$

$$\Rightarrow V_1 = \frac{80}{3}V$$

• The voltage across series branch 10 Ω resistor is

$$V_{10 \Omega} = (-4)(10) = -40V$$

• There are two meshes in the above circuit. The KVL equation around second mesh is

$$V_1 - V_{10 \Omega} - V_{Th} = 0$$

• Substitute the values of $V_1$ and $V_{10 \Omega}$ in the above equation.

$$\frac{80}{3} - (-40) - V_{Th} = 0$$

$$V_{Th} = \frac{80 + 120}{3} = \frac{200}{3}V$$

• Therefore, the Thevenin’s voltage is $V_{Th} = \frac{200}{3}V$

Step 3 − Calculation of Thevenin’s resistance R_Th.

Short circuit the voltage source and open circuit the current source of the above circuit in order to calculate the Thevenin’s resistance R_Th across the terminals A & B. The modified circuit diagram is shown in the following figure.

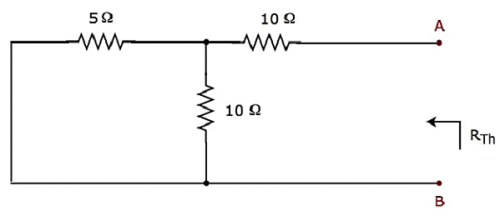
The Thevenin’s resistance across terminals A & B will be

$$R_{Th} = \lgroup \frac{5 \times 10}{5 + 10} \rgroup + 10 = \frac{10}{3} + 10 = \frac{40}{3} \Omega$$

Therefore, the Thevenin’s resistance is $\mathbf {R_{Th} = \frac{40}{3} \Omega}$.

Step 4 − The Thevenin’s equivalent circuit is placed to the left of terminals A & B in the given circuit. This circuit diagram is shown in the following figure.

The current flowing through the 20 Ω resistor can be found by substituting the values of V_Th, R_Th and R in the following equation.

$$l = \frac{V_{Th}}{R_{Th} + R}$$

$$l = \frac{\frac{200}{3}}{\frac{40}{3} + 20} = \frac{200}{100} = 2A$$

Therefore, the current flowing through the 20 Ω resistor is 2 A.

Method 2

Follow these steps in order to find the Thevenin’s equivalent circuit, when the sources of both independent type and dependent type are present.

• Step 1 − Consider the circuit diagram by opening the terminals with respect to which, the Thevenin’s equivalent circuit is to be found.

• Step 2 − Find Thevenin’s voltage V_Th across the open terminals of the above circuit.

• Step 3 − Find the short circuit current I_SC by shorting the two opened terminals of the above circuit.

• Step 4 − Find Thevenin’s resistance R_Th by using the following formula.

$$R_{Th} = \frac{V_{Th}}{I_{SC}}$$

Step 5 − Draw the Thevenin’s equivalent circuit by connecting a Thevenin’s voltage V_Th in series with a Thevenin’s resistance R_Th.

Now, we can find the response in an element that lies to the right side of the Thevenin’s equivalent circuit.

Norton’s theorem is similar to Thevenin’s theorem. It states that any two terminal linear network or circuit can be represented with an equivalent network or circuit, which consists of a current source in parallel with a resistor. It is known as Norton’s equivalent circuit. A linear circuit may contain independent sources, dependent sources and resistors.

If a circuit has multiple independent sources, dependent sources, and resistors, then the response in an element can be easily found by replacing the entire network to the left of that element with a Norton’s equivalent circuit.

The response in an element can be the voltage across that element, current flowing through that element or power dissipated across that element.

This concept is illustrated in following figures.

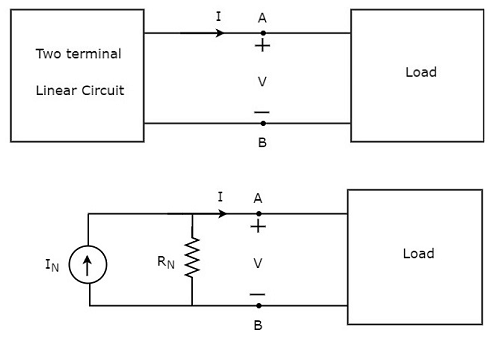
Norton’s equivalent circuit resembles a practical current source. Hence, it is having a current source in parallel with a resistor.

• The current source present in the Norton’s equivalent circuit is called as Norton’s equivalent current or simply Norton’s current I_N.

• The resistor present in the Norton’s equivalent circuit is called as Norton’s equivalent resistor or simply Norton’s resistor R_N.

Methods of Finding Norton’s Equivalent Circuit

There are three methods for finding a Norton’s equivalent circuit. Based on the type of sources that are present in the network, we can choose one of these three methods. Now, let us discuss these three methods one by one.

Method 1

Follow these steps in order to find the Norton’s equivalent circuit, when only the sources of independent type are present.

• Step 1 − Consider the circuit diagram by opening the terminals with respect to which, the Norton’s equivalent circuit is to be found.

• Step 2 − Find the Norton’s current I_N by shorting the two opened terminals of the above circuit.

• Step 3 − Find the Norton’s resistance R_N across the open terminals of the circuit considered in Step1 by eliminating the independent sources present in it. Norton’s resistance R_N will be same as that of Thevenin’s resistance R_Th.

• Step 4 − Draw the Norton’s equivalent circuit by connecting a Norton’s current IN in parallel with Norton’s resistance R_N.

Now, we can find the response in an element that lies to the right side of Norton’s equivalent circuit.

Method 2

Follow these steps in order to find the Norton’s equivalent circuit, when the sources of both independent type and dependent type are present.

• Step 1 − Consider the circuit diagram by opening the terminals with respect to which the Norton’s equivalent circuit is to be found.

• Step 2 − Find the open circuit voltage V_OC across the open terminals of the above circuit.

• Step 3 − Find the Norton’s current I_N by shorting the two opened terminals of the above circuit.

• Step 4 − Find Norton’s resistance R_N by using the following formula.

$$R_N = \frac{V_{OC}}{I_N}$$

• Step 5 − Draw the Norton’s equivalent circuit by connecting a Norton’s current I_N in parallel with Norton’s resistance R_N.

Now, we can find the response in an element that lies to the right side of Norton’s equivalent circuit.

Method 3

This is an alternate method for finding a Norton’s equivalent circuit.

• Step 1 − Find a Thevenin’s equivalent circuit between the desired two terminals. We know that it consists of a Thevenin’s voltage source, V_Th and Thevenin’s resistor, R_Th.

• Step 2 − Apply source transformation technique to the above Thevenin’s equivalent circuit. We will get the Norton’s equivalent circuit. Here,

Norton’s current,

$$I_N = \frac{V_{Th}}{R_{Th}}$$

Norton’s resistance,

$$R_N = R_{Th}$$

This concept is illustrated in the following figure.

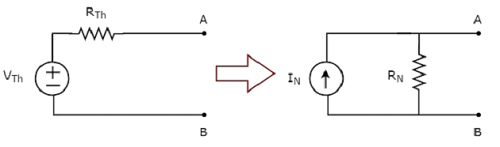
Now, we can find the response in an element by placing Norton’s equivalent circuit to the left of that element.

Note − Similarly, we can find the Thevenin’s equivalent circuit by finding a Norton’s equivalent circuit first and then apply source transformation technique to it. This concept is illustrated in the following figure.

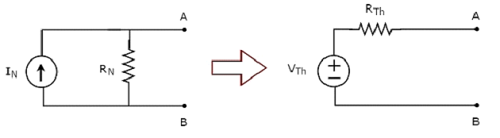
This is the Method 3 for finding a Thevenin’s equivalent circuit.

Example

Find the current flowing through 20 Ω resistor by first finding a Norton’s equivalent circuit to the left of terminals A and B.

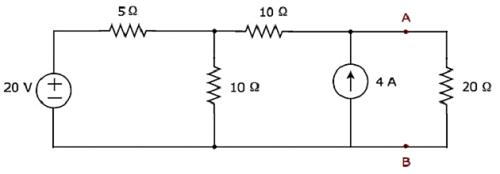
Let us solve this problem using Method 3.

Step 1 − In previous chapter, we calculated the Thevenin’s equivalent circuit to the left side of terminals A & B. We can use this circuit now. It is shown in the following figure.

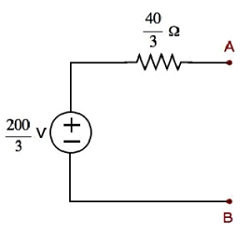
Here, Thevenin’s voltage, $V_{Th} = \frac{200}{3} V$ and Thevenin’s resistance, $R_{Th} = \frac{40}{3} \Omega$

Step 2 − Apply source transformation technique to the above Thevenin’s equivalent circuit. Substitute the values of V_Th and R_Th in the following formula of Norton’s current.

$$I_N = \frac{V_{Th}}{R_{Th}}$$

$$I_N = \frac{\frac{200}{3}}{\frac{40}{3}} = 5A$$

Therefore, Norton’s current I_N is 5 A.

We know that Norton’s resistance, R_N is same as that of Thevenin’s resistance R_Th.

$$\mathbf {R_N = \frac{40}{3} \Omega}$$

The Norton’s equivalent circuit corresponding to the above Thevenin’s equivalent circuit is shown in the following figure.

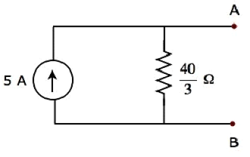
Now, place the Norton’s equivalent circuit to the left of the terminals A & B of the given circuit.

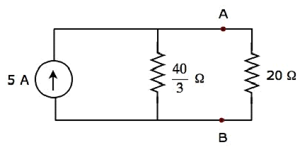
By using current division principle, the current flowing through the 20 Ω resistor will be

$$I_{20 \Omega} = 5 \lgroup \frac{\frac{40}{3}}{\frac{40}{3} + 20} \rgroup$$

$$I_{20 \Omega} = 5 \lgroup \frac{40}{100} \rgroup = 2A$$

Therefore, the current flowing through the 20 Ω resistor is 2 A.

The amount of power received by a load is an important parameter in electrical and electronic applications. In DC circuits, we can represent the load with a resistor having resistance of R_L ohms. Similarly, in AC circuits, we can represent it with a complex load having an impedance of Z_L ohms.

Maximum power transfer theorem states that the DC voltage source will deliver maximum power to the variable load resistor only when the load resistance is equal to the source resistance.

Similarly, Maximum power transfer theorem states that the AC voltage source will deliver maximum power to the variable complex load only when the load impedance is equal to the complex conjugate of source impedance.

In this chapter, let us discuss about the maximum power transfer theorem for DC circuits.

Proof of Maximum Power Transfer Theorem

Replace any two terminal linear network or circuit to the left side of variable load resistor having resistance of R_L ohms with a Thevenin’s equivalent circuit. We know that Thevenin’s equivalent circuit resembles a practical voltage source.

This concept is illustrated in following figures.

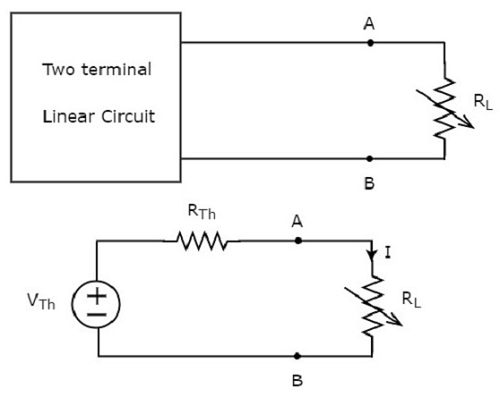
The amount of power dissipated across the load resistor is

$$P_L = I^2 R_L$$

Substitute $I = \frac{V_{Th}}{R_{Th} + R_L}$ in the above equation.

$$P_L = \lgroup \frac{V_{Th}}{(R_{Th} + R_L)} \rgroup ^2 R_L$$

$\Rightarrow P_L = {V_{Th}}^2 \lbrace \frac{R_L}{(R_{Th} + R_L)^2} \rbrace$ Equation 1

Condition for Maximum Power Transfer

For maximum or minimum, first derivative will be zero. So, differentiate Equation 1 with respect to R_L and make it equal to zero.

$$\frac{dP_L}{dR_L} = {V_{Th}}^2 \lbrace \frac{(R_{Th} + R_L)^2 \times 1 - R_L \times 2(R_{Th} + R_L)}{(R_{Th} + R_L)^4} \rbrace = 0$$

$$\Rightarrow (R_{Th} + R_L)^2 -2R_L(R_{Th} + R_L) = 0$$

$$\Rightarrow (R_{Th} + R_L)(R_{Th} + R_L - 2R_L) = 0$$

$$\Rightarrow (R_{Th} - R_L) = 0$$

$$\Rightarrow R_{Th} = R_L\:or\:R_L = R_{Th}$$

Therefore, the condition for maximum power dissipation across the load is $R_L = R_{Th}$. That means, if the value of load resistance is equal to the value of source resistance i.e., Thevenin’s resistance, then the power dissipated across the load will be of maximum value.

The value of Maximum Power Transfer

Substitute $R_L = R_{Th}\:\&\:P_L = P_{L, Max}$ in Equation 1.

$$P_{L, Max} = {V_{Th}}^2 \lbrace \frac{R_{Th}}{(R_{Th} + R_{Th})^2} \rbrace$$

$$P_{L, Max} = {V_{Th}}^2 \lbrace \frac{R_{Th}}{4 {R_{Th}}^2} \rbrace$$

$$\Rightarrow P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{Th}}$$

$$\Rightarrow P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{L}}, \: since \: R_{L} = R_{Th}$$

Therefore, the maximum amount of power transferred to the load is

$$P_{L, Max} = \frac{{V_{Th}}^2}{4R_{L}} = \frac{{V_{Th}}^2}{4R_{Th}}$$

Efficiency of Maximum Power Transfer

We can calculate the efficiency of maximum power transfer, $\eta_{Max}$ using following formula.

$\eta_{Max} = \frac{P_{L, Max}}{P_S}$ Equation 2

Where,

• $P_{L, Max}$ is the maximum amount of power transferred to the load.

• $P_S$ is the amount of power generated by the source.

The amount of power generated by the source is

$$P_S = I^2 R_{Th} + I^2 R_L$$

$$\Rightarrow P_S = 2 I^2 R_{Th},\:since\:R_{L} = R_{Th}$$

• Substitute $I = \frac{V_{Th}}{2 R_{Th}}$ in the above equation.

$$P_S = 2\lgroup \frac{V_{Th}}{2 R_{Th}} \rgroup ^2 R_{Th}$$

$$\Rightarrow P_S = 2\lgroup \frac{{V_{Th}}^2}{4 {R_{Th}}^2} \rgroup R_{Th}$$

$$\Rightarrow P_S = \frac{{V_{Th}}^2}{2 R_{Th}}$$

• Substitute the values of $P_{L, Max}$ and $P_S$ in Equation 2.

$$\eta_{Max} = \frac{\lgroup \frac{{V_{Th}}^2}{4R_{Th}} \rgroup}{\lgroup \frac{{V_{Th}}^2}{2R_{Th}}\rgroup}$$

$$\Rightarrow \eta_{Max} = \frac{1}{2}$$

We can represent the efficiency of maximum power transfer in terms of percentage as follows −

$$\% \eta_{Max} = \eta_{Max} \times 100\%$$

$$\Rightarrow \% \eta_{Max} = \lgroup \frac{1}{2} \rgroup \times 100\%$$

$$\Rightarrow \% \eta_{Max} = 50\%$$

Therefore, the efficiency of maximum power transfer is 50 %.

Example

Find the maximum power that can be delivered to the load resistor R_L of the circuit shown in the following figure.

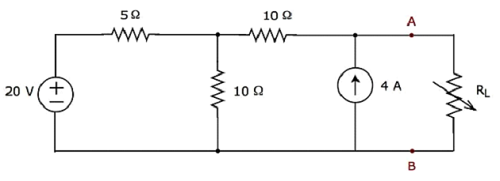
Step 1 − In Thevenin’s Theorem chapter, we calculated the Thevenin’s equivalent circuit to the left side of terminals A & B. We can use this circuit now. It is shown in the following figure.

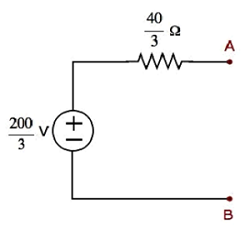
Here, Thevenin’s voltage $V_{Th} = \frac{200}{3}V$ and Thevenin’s resistance $R_{Th} = \frac{40}{3} \Omega$

Step 2 − Replace the part of the circuit, which is left side of terminals A & B of the given circuit with the above Thevenin’s equivalent circuit. The resultant circuit diagram is shown in the following figure.

Step 3- Mit der folgenden Formel können wir die maximale Leistung ermitteln, die an den Lastwiderstand R _{L abgegeben} wird.

$$P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{Th}}$$

Ersatz $V_{Th} = \frac{200}{3}V$ und $R_{Th} = \frac{40}{3} \Omega$ in der obigen Formel.

$$P_{L, Max} = \frac{\lgroup \frac{200}{3} \rgroup ^ 2}{4 \lgroup \frac{40}{3}\rgroup } $$

$$P_{L, Max} = \frac{250}{3} W$$

deshalb, die maximum power das wird an den Lastwiderstand RL der gegebenen Schaltung geliefert $\mathbf {\frac{250}{3}}$ W

Wenn sich der Ausgang eines Stromkreises für einen Eingang zeitlich ändert, spricht man von time response. Das Zeitverhalten besteht aus folgenden zwei Teilen.

• Einschwingverhalten
• Steady-State-Antwort

Lassen Sie uns in diesem Kapitel zunächst diese beiden Reaktionen diskutieren und dann diese beiden Reaktionen in einer Serien-RL-Schaltung beobachten, wenn sie von einer Gleichspannungsquelle angeregt wird.

Einschwingverhalten

Nach dem Anlegen eines Eingangs an einen Stromkreis benötigt der Ausgang eine gewisse Zeit, um den stationären Zustand zu erreichen. Der Ausgang befindet sich also im Übergangszustand, bis er in einen stabilen Zustand übergeht. Daher ist die Reaktion des Stromkreises während des Übergangszustands bekannt alstransient response.

Das Einschwingverhalten ist für große Werte von 't' Null. Idealerweise sollte dieser Wert von 't' unendlich sein. Aber praktischfive time constants sind ausreichend.

Vorhandensein oder Nichtvorhandensein von Transienten

Transienten treten in der Antwort aufgrund von auf sudden changein den Quellen, die an den Stromkreis angelegt werden und / oder aufgrund von Schaltvorgängen. Es gibt zwei mögliche Schaltvorgänge. Das sind Öffnungsschalter und Schließschalter.

• Das transient Teil wird not presentin der Reaktion eines Stromkreises oder Netzwerks, wenn es nur Widerstände enthält. weilresistor hat die Fähigkeit, jede Menge an Spannung und Strom einzustellen.

• Das transient part occurs in der Reaktion eines Stromkreises oder Netzwerks aufgrund des Vorhandenseins von Energiespeicherelementen wie z inductor and capacitor. Weil sie die in diesen Elementen gespeicherte Energie nicht sofort ändern können.

Induktorverhalten

Angenommen, die Schaltaktion findet bei t = 0 statt.Inductor currentändert sich nicht sofort, wenn die Schaltaktion stattfindet. Das heißt, der Wert des Induktivitätsstroms unmittelbar nach dem Schaltvorgang ist der gleiche wie der unmittelbar vor dem Schaltvorgang.

Mathematisch kann es dargestellt werden als

$$i_L (0^+) = i_L (0^-)$$

Kondensatorverhalten

Das capacitor voltageändert sich nicht augenblicklich ähnlich wie der Induktivitätsstrom, wenn die Schaltaktion stattfindet. Das heißt, der Wert der Kondensatorspannung unmittelbar nach dem Schaltvorgang ist der gleiche wie der unmittelbar vor dem Schaltvorgang.

Mathematisch kann es dargestellt werden als

$$v_c (0^+) = v_c (0^-)$$

Steady-State-Antwort

Der Teil der Zeitantwort, der auch dann verbleibt, wenn die Übergangsantwort für große Werte von 't' Null geworden ist, ist bekannt als steady state response. Dies bedeutet, dass im eingeschwungenen Zustand kein vorübergehender Teil der Reaktion vorhanden ist.

Induktorverhalten

Wenn die unabhängige Quelle über einen längeren Zeitraum mit einem oder mehreren Induktivitäten und Widerständen (optional) an den Stromkreis oder das Netzwerk angeschlossen ist, befindet sich dieser Stromkreis oder dieses Netzwerk im eingeschwungenen Zustand. Daher ist die in den Induktoren dieses Stromkreises gespeicherte Energie maximal und konstant.

Mathematisch kann es dargestellt werden als

$W_L = \frac{L {i_L}^2}{2} = $ Maximum & Konstante

$\Rightarrow i_L = $ Maximum & Konstante

Daher wirkt der Induktor als constant current source im eingeschwungenen Zustand.

Die Spannung am Induktor beträgt

$$V_L = L \frac{di_{L}}{dt} = 0V$$

Der Induktor wirkt also als short circuit im eingeschwungenen Zustand.

Kondensatorverhalten

Wenn die unabhängige Quelle über einen längeren Zeitraum mit einem oder mehreren Kondensatoren und Widerständen (optional) an den Stromkreis oder das Netzwerk angeschlossen ist, befindet sich dieser Stromkreis oder dieses Netzwerk im eingeschwungenen Zustand. Daher ist die in den Kondensatoren dieses Stromkreises gespeicherte Energie maximal und konstant.

Mathematisch kann es dargestellt werden als

$W_c = \frac{C{v_c}^2}{2} = $ Maximum & Konstante

$\Rightarrow v_c = $Maximum & Konstante

Daher wirkt der Kondensator als constant voltage source im eingeschwungenen Zustand.

Der durch den Kondensator fließende Strom wird sein

$$i_c = C\frac{dv_c}{dt} = 0A$$

Der Kondensator wirkt also als open circuit im eingeschwungenen Zustand.

Ermitteln der Reaktion der Serie RL-Schaltung

Folgendes berücksichtigen series RL circuit Diagramm.

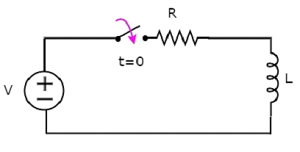
In der obigen Schaltung ist die switch wurde behalten openbis zu t = 0 und es wurde bei t = 0 geschlossen. Daher ist die Gleichspannungsquelle mit V Volt bis zu diesem Zeitpunkt nicht mit der Serien-RL-Schaltung verbunden. Daher gibt esno initial current fließt durch Induktor.

Der Schaltplan, wenn die switch ist in closed Die Position ist in der folgenden Abbildung dargestellt.

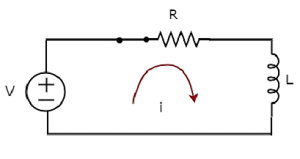
Nun der Strom i fließt in der gesamten Schaltung, da die Gleichspannungsquelle mit V Volt ist an die Serien-RL-Schaltung angeschlossen.

Bewerben Sie sich jetzt KVL um die Schleife.

$$V = Ri + L \frac{di}{dt}$$

$\frac{di}{dt} + \lgroup \frac{R}{L} \rgroup i = \frac{V}{L}$Equation 1

Die obige Gleichung ist eine Differentialgleichung erster Ordnung und liegt in Form von vor

$\frac{dy}{dt} + Py = Q$Equation 2

Durch comparing Gleichung 1 und Gleichung 2 erhalten wir die folgenden Beziehungen.

$$x = t$$

$$y = i$$

$$P = \frac{R}{L}$$

$$Q = \frac{V}{L}$$

Das solution von Gleichung 2 wird sein

$ye^{\int p dx} = \int Q e^{\int p dx} dx + k$Equation 3

Wo, k ist die Konstante.

Ersetzen Sie die Werte von x, y, P & Q in Gleichung 3.

$ie^{\int {\lgroup \frac{R}{L} \rgroup}dt} = \int (\frac{V}{L}) \lgroup e^{\int {\lgroup \frac{R}{L} \rgroup}dt} \rgroup dt + k$

$\Rightarrow ie^{\lgroup \frac{R}{L} \rgroup t} = \frac{V}{L} \int e^{\lgroup \frac{R}{L} \rgroup t} dt + k$

$\Rightarrow ie^{\lgroup \frac{R}{L} \rgroup t} = \frac{V}{L} \lbrace \frac{e^{\lgroup \frac{R}{L} \rgroup}t}{\frac{R}{L}} \rbrace + k$

$\Rightarrow i = \frac{V}{R} + k e^{-\lgroup \frac{R}{L} \rgroup}t$Equation 4

Wir wissen, dass in der Schaltung kein Anfangsstrom vorhanden ist. Ersetzen Sie daher t = 0 und = 0 in Gleichung 4, um den Wert der Konstante zu finden k.

$$0 = \frac{V}{R} + ke^{-\lgroup \frac{R}{L} \rgroup(0)}$$

$$0 = \frac{V}{R} + k(1)$$

$$k = - \frac{V}{R}$$

Ersetzen Sie den Wert von k in Gleichung 4.

$$i = \frac{V}{R} + \lgroup - \frac{V}{R} \rgroup e^{-\lgroup \frac{R}{L} \rgroup t}$$

$$i = \frac{V}{R} - \frac{V}{R}e^{-\lgroup \frac{R}{L} \rgroup t}$$

deshalb, die current durch den Stromkreis fließen ist

$i = - \frac{V}{R}e^{-\lgroup \frac{R}{L} \rgroup t} + \frac{V}{R}$Equation 5

Die Antwort der Serien-RL-Schaltung, wenn sie von einer Gleichspannungsquelle angeregt wird, hat also die folgenden zwei Terme.

• Die erste Amtszeit $-\frac{V}{R}e^{-\lgroup \frac{R}{L} \rgroup t}$ entspricht dem transient response.

• Die zweite Amtszeit $\frac{V}{R}$ entspricht dem steady state response. Diese beiden Antworten sind in der folgenden Abbildung dargestellt.

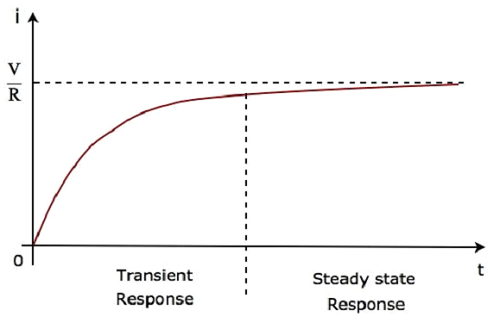
Wir können die Gleichung 5 wie folgt umschreiben:

$i = \frac{V}{R} \lgroup 1 - e^{-\lgroup \frac{R}{L} \rgroup t} \rgroup$

$\Rightarrow i = \frac{V}{R} \lgroup 1 - e^{-\lgroup \frac{t}{\tau} \rgroup} \rgroup$Equation 6

Wo, τ ist der time constant und sein Wert ist gleich $\frac{L}{R}$.

Sowohl Gleichung 5 als auch Gleichung 6 sind gleich. Wir können jedoch die obige Wellenform des durch die Schaltung fließenden Stroms aus Gleichung 6 leicht verstehen, indem wir einige Werte von einsetzent wie 0, τ, 2τ, 5τ usw.

In der obigen Wellenform des durch die Schaltung fließenden Stroms zeigt das Einschwingverhalten bis zu fünf Zeitkonstanten ab Null, während das stationäre Verhalten ab fünf Zeitkonstanten vorliegt.

Im vorherigen Kapitel haben wir das Einschwingverhalten und das stationäre Verhalten des Gleichstromkreises erörtert. Lassen Sie uns in diesem Kapitel das diskutierenresponse of AC circuit. Die Konzepte des Einschwingverhaltens und des stationären Ansprechverhaltens, die wir im vorherigen Kapitel erörtert haben, werden auch hier nützlich sein.

Ermitteln der Reaktion der Serie RL-Schaltung

Folgendes berücksichtigen series RL circuit Diagramm.

In der obigen Schaltung ist die switch wurde behalten openbis zu t = 0 und es wurde bei t = 0 geschlossen . Daher ist die Wechselspannungsquelle mit einer Spitzenspannung von V _m Volt bis zu diesem Zeitpunkt nicht mit der Serien-RL-Schaltung verbunden. Daher gibt esno initial current fließt durch den Induktor.

Der Schaltplan, wenn die switch ist in closed Position, ist in der folgenden Abbildung dargestellt.

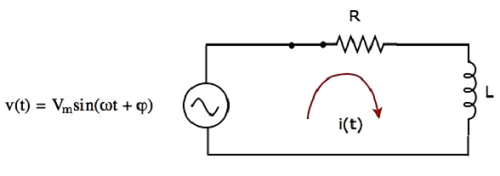
Nun fließt der Strom i (t) in der gesamten Schaltung, da die Wechselspannungsquelle mit einer Spitzenspannung von V _m Volt an die Serien-RL-Schaltung angeschlossen ist.

Wir wissen, dass der Strom i (t) , der durch die obige Schaltung fließt, zwei Terme hat, einen, der den Übergangsteil darstellt, und einen anderen Term, der den stationären Zustand darstellt.

Mathematisch kann es dargestellt werden als

$i(t) = i_{Tr}(t) + i_{ss}(t)$Equation 1

Wo,

• $i_{Tr}(t)$ ist das Einschwingverhalten des durch die Schaltung fließenden Stroms.

• $i_{ss}(t)$ ist die stationäre Reaktion des durch die Schaltung fließenden Stroms.

Im vorherigen Kapitel haben wir das Einschwingverhalten des durch die Serien-RL-Schaltung fließenden Stroms erhalten. Es ist in Form von$Ke^{-\lgroup \frac{t}{\tau} \rgroup}$.

Ersatz $i_{Tr}(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup}$ in Gleichung 1.

$i(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup} + i_{ss}(t)$Equation 2

Berechnung des stationären Stroms

Wenn ein sinusförmiges Signal als Eingang für einen linearen Stromkreis angelegt wird, erzeugt es einen stationären Ausgang, der auch a ist sinusoidal signal. Sowohl das sinusförmige Eingangs- als auch das Ausgangssignal haben die gleiche Frequenz, jedoch unterschiedliche Amplituden und Phasenwinkel.

Wir können die stationäre Reaktion eines Stromkreises berechnen, wenn er von einer sinusförmigen Spannungsquelle mit angeregt wird Laplace Transform approach.

Das S-Domänen-Schaltbild, wenn die switch ist in closed Position, ist in der folgenden Abbildung dargestellt.

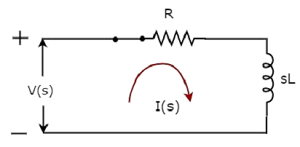
In der obigen Schaltung sind alle Größen und Parameter in dargestellt s-domain. Dies sind die Laplace-Transformationen von Zeitbereichsgrößen und -parametern.

Das Transfer function der obigen Schaltung ist

$$H(s) = \frac{I(s)}{V(s)}$$

$$\Rightarrow H(s) = \frac{1}{Z(s)}$$

$$\Rightarrow H(s) = \frac{1}{R + sL}$$

Ersatz $s = j \omega$ in der obigen Gleichung.

$$H(j \omega) = \frac{1}{R + j \omega L}$$

Magnitude of $\mathbf{\mathit{H(j \omega)}}$ ist

$$|H(j \omega)| = \frac{1}{\sqrt{R^2 + {\omega}^2}L^2}$$

Phase angle of $\mathbf{\mathit{H(j \omega)}}$ ist

$$\angle H(j \omega) = -tan^{-1} \lgroup \frac{\omega L}{R} \rgroup$$

Wir werden das bekommen steady state current $i_{ss}(t)$ indem Sie die folgenden zwei Schritte ausführen -

• Multiplizieren Sie die Spitzenspannung der sinusförmigen Eingangsspannung und die Größe von $H(j \omega)$.

• Addieren Sie die Phasenwinkel der sinusförmigen Eingangsspannung und $H(j \omega)$.

Das steady state current $i_{ss}(t)$ wird sein

$$i_{ss}(t) = \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$

Ersetzen Sie den Wert von $i_{ss}(t)$ in Gleichung 2.

$i(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$Equation 3

Wir wissen, dass in der Schaltung kein Anfangsstrom vorhanden ist. Ersetzen Sie daher in Gleichung 3 t = 0 & i (t) = 0 , um den Wert der Konstanten K zu ermitteln.

$$0 = Ke^{-\lgroup \frac{0}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega (0) + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$

$$\Rightarrow 0 = K + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$

$$\Rightarrow K = - \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$

Ersetzen Sie den Wert von K in Gleichung 3.

$i(t) = - \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup e^{-\lgroup \frac{t}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$Equation 4

Gleichung 4 stellt den Strom dar, der durch die Serien-RL-Schaltung fließt, wenn er von einer sinusförmigen Spannungsquelle angeregt wird. Es hat zwei Begriffe. Der erste und der zweite Term repräsentieren das Einschwingverhalten bzw. das stationäre Ansprechverhalten des Stroms.

Wir können neglect the first termvon Gleichung 4, weil sein Wert sehr viel kleiner als eins sein wird. Der resultierende Strom, der durch die Schaltung fließt, ist also

$$i(t) = \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$

Es enthält nur die steady state term. Daher können wir nur das stationäre Verhalten von Wechselstromkreisen finden und das Einschwingverhalten vernachlässigen.

Resonancetritt in elektrischen Schaltkreisen aufgrund des Vorhandenseins von Energiespeicherelementen wie Induktor und Kondensator auf. Es ist das grundlegende Konzept, auf dessen Grundlage die Radio- und Fernsehempfänger so ausgelegt sind, dass sie nur die gewünschte Senderfrequenz auswählen können.

Es gibt two typesvon Resonanzen, nämlich Serienresonanz und Parallelresonanz. Diese werden anhand der Netzwerkelemente klassifiziert, die in Reihe oder parallel geschaltet sind. Lassen Sie uns in diesem Kapitel die Serienresonanz diskutieren.

Serienresonanz-Schaltplan

Wenn die Resonanz in einer Reihen-RLC-Schaltung auftritt, wird sie als bezeichnet Series Resonance. Folgendes berücksichtigenseries RLC circuit, die in der Zeigerdomäne dargestellt wird.

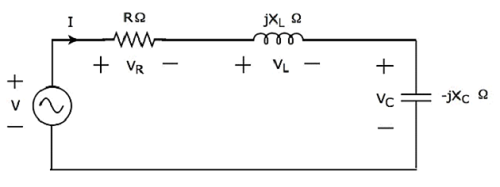
Hier sind die passiven Elemente wie Widerstand, Induktivität und Kondensator in Reihe geschaltet. Diese gesamte Kombination ist inseries mit der sinusförmigen Eingangsspannungsquelle.

Anwenden KVL um die Schleife.

$$V - V_R - V_L - V_C = 0$$

$$\Rightarrow V - IR - I(j X_L) - I(-j X_C) = 0$$

$$\Rightarrow V = IR + I(j X_L) + I(-j X_C)$$

$\Rightarrow V = I[R + j(X_L - X_C)]$Equation 1

Die obige Gleichung hat die Form von V = IZ.

deshalb, die impedance Z der Serie RLC-Schaltung wird sein

$$Z = R + j(X_L - X_C)$$

Parameter und elektrische Größen bei Resonanz

Lassen Sie uns nun die Werte der Parameter und elektrischen Größen bei Resonanz der Serien-RLC-Schaltung nacheinander ableiten.

Resonanzfrequenz

Die Frequenz, bei der Resonanz auftritt, wird als bezeichnet resonant frequency f_r. In Serie RLC tritt eine Resonanz auf, wenn der imaginäre Impedanzterm Z Null ist, dh der Wert von$X_L - X_C$ sollte gleich Null sein.

$$\Rightarrow X_L = X_C$$

Ersatz $X_L = 2 \pi f L$ und $X_C = \frac{1}{2 \pi f C}$ in der obigen Gleichung.

$$2 \pi f L = \frac{1}{2 \pi f C}$$

$$\Rightarrow f^2 = \frac{1}{(2 \pi)^2 L C}$$

$$\Rightarrow f = \frac{1}{(2 \pi) \sqrt{LC}}$$

deshalb, die resonant frequency f_r der Serie RLC-Schaltung ist

$$f_r = \frac{1}{(2 \pi) \sqrt{LC}}$$

Wo, L ist die Induktivität eines Induktors und C ist die Kapazität eines Kondensators.

Das resonant frequency f_r der Serien-RLC-Schaltung hängt nur von der Induktivität ab L und Kapazität C. Aber es ist unabhängig vom WiderstandR.

Impedanz

Wir haben die impedance Z der Serien-RLC-Schaltung als

$$Z = R + j(X_L - X_C)$$

Ersatz $X_L = X_C$ in der obigen Gleichung.

$$Z = R + j(X_C - X_C)$$

$$\Rightarrow Z = R + j(0)$$

$$\Rightarrow Z = R$$

Bei Resonanz wird die impedance Z der Serien-RLC-Schaltung ist gleich dem Widerstandswert Rdh Z = R.

Strom fließt durch den Stromkreis

Ersatz $X_L - X_C = 0$ in Gleichung 1.

$$V = I[R + j(0)]$$

$$\Rightarrow V = IR$$

$$\Rightarrow I = \frac{V}{R}$$

Deshalb, current Durchfluss durch Serien-RLC-Schaltung bei Resonanz ist $\mathbf{\mathit{I = \frac{V}{R}}}$.

Bei Resonanz erreicht die Impedanz der Serien-RLC-Schaltung einen Minimalwert. Daher diemaximum current fließt durch diesen Stromkreis bei Resonanz.

Spannung am Widerstand

Die Spannung am Widerstand beträgt

$$V_R = IR$$

Ersetzen Sie den Wert von I in der obigen Gleichung.

$$V_R = \lgroup \frac{V}{R} \rgroup R$$

$$\Rightarrow V_R = V$$

deshalb, die voltage across resistor bei Resonanz ist V_R = V.

Spannung am Induktor

Die Spannung am Induktor beträgt

$$V_L = I(jX_L)$$

Ersetzen Sie den Wert von I in der obigen Gleichung.

$$V_L = \lgroup \frac{V}{R} \rgroup (jX_L)$$

$$\Rightarrow V_L = j \lgroup \frac{X_L}{R} \rgroup V$$

$$\Rightarrow V_L = j QV$$

deshalb, die voltage across inductor bei Resonanz ist $V_L = j QV$.

Also, die magnitude der Spannung über Induktor bei Resonanz wird sein

$$|V_L| = QV$$

Wo Q ist der Quality factor und sein Wert ist gleich $\frac{X_L}{R}$

Spannung am Kondensator

Die Spannung am Kondensator beträgt

$$V_C = I(-j X_C)$$

Ersetzen Sie den Wert von I in der obigen Gleichung.

$$V_C = \lgroup \frac{V}{R} \rgroup (-j X_C)$$

$$\Rightarrow V_C = -j \lgroup \frac{X_C}{R} \rgroup V$$

$$\Rightarrow V_C = -jQV$$

deshalb, die voltage across capacitor bei Resonanz ist $\mathbf{\mathit{V_C = -jQV}}$.

Also, die magnitude der Spannung über dem Kondensator bei Resonanz wird sein

$$|V_C| = QV$$

Wo Q ist der Quality factor und sein Wert ist gleich $\frac{X_{C}}{R}$

Note - Die Serienresonanz-RLC-Schaltung wird als bezeichnet voltage magnificationSchaltung, weil die Größe der Spannung über der Induktivität und dem Kondensator gleich dem Q- fachen der sinusförmigen Eingangsspannung V ist .

Im vorherigen Kapitel haben wir die Bedeutung der Serienresonanz erörtert. Lassen Sie uns nun die Parallelresonanz in RLC-Schaltkreisen diskutieren.

Parallelresonanz-Schaltplan

Wenn die Resonanz in einer parallelen RLC-Schaltung auftritt, wird sie als bezeichnet Parallel Resonance. Folgendes berücksichtigenparallel RLC circuit, die in der Zeigerdomäne dargestellt wird.

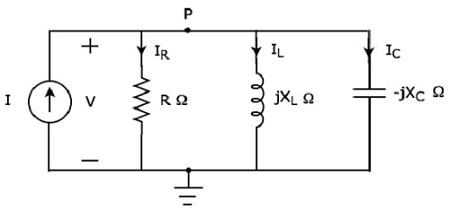
Hier sind die passiven Elemente wie Widerstand, Induktivität und Kondensator parallel geschaltet. Diese gesamte Kombination ist inparallel mit der sinusförmigen Eingangsstromquelle.

Schreiben nodal equation am Knoten P.

$$- I + I_R + I_L + I_C = 0$$

$$\Rightarrow - I + \frac{V}{R} + \frac{V}{j X_L} + \frac{V}{-j X_C} = 0$$

$$\Rightarrow I = \frac{V}{R} - \frac{jV}{X_L} + \frac{jV}{X_C}$$

$\Rightarrow I = V[\frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_L} \rgroup]$Equation 1

Die obige Gleichung hat die Form von I = VY.

deshalb, die admittance Y der parallelen RLC-Schaltung wird

$$Y = \frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_L} \rgroup$$

Parameter und elektrische Größen bei Resonanz

Lassen Sie uns nun die Werte der Parameter und elektrischen Größen bei Resonanz der parallelen RLC-Schaltung nacheinander ableiten.

Resonanzfrequenz

Wir wissen, dass die resonant frequency, f_rist die Frequenz, bei der Resonanz auftritt. Im parallelen RLC-Schaltkreis tritt Resonanz auf, wenn der imaginäre Admittanzterm Y Null ist. dh der Wert von$\frac{1}{X_C} - \frac{1}{X_L}$ sollte gleich Null sein

$$\Rightarrow \frac{1}{X_C} = \frac{1}{X_L}$$

$$\Rightarrow X_L = X_C$$

Die obige Resonanzbedingung ist dieselbe wie die der Serien-RLC-Schaltung. Also, dieresonant frequency, f_r ist sowohl in der Serien-RLC-Schaltung als auch in der Parallel-RLC-Schaltung gleich.

deshalb, die resonant frequency, f_r der parallelen RLC-Schaltung ist

$$f_r = \frac{1}{2 \pi \sqrt{LC}}$$

Wo,

• L ist die Induktivität eines Induktors.
• C ist die Kapazität eines Kondensators.

Das resonant frequency, f_r der parallelen RLC-Schaltung hängt nur von der Induktivität ab L und Kapazität C. Aber es ist unabhängig vom WiderstandR.

Zulassung

Wir haben die admittance Y der parallelen RLC-Schaltung als

$$Y = \frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_L} \rgroup$$

Ersatz, $X_L = X_C$ in der obigen Gleichung.

$$Y = \frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_C} \rgroup$$

$$\Rightarrow Y = \frac{1}{R} + j(0)$$

$$\Rightarrow Y = \frac{1}{R}$$

Bei Resonanz wird die admittance, Y der parallelen RLC-Schaltung ist gleich dem Kehrwert des Widerstands, R, dh $\mathbf{\mathit{Y = \frac{1}{R}}}$

Spannung an jedem Element

Ersatz, $\frac{1}{X_C} - \frac{1}{X_L} = 0$ in Gleichung 1

$$I = V [\frac{1}{R} + j(0)]$$

$$\Rightarrow I = \frac{V}{R}$$

$$\Rightarrow V = IR$$

deshalb, die voltage über alle Elemente der parallelen RLC-Schaltung bei Resonanz ist V = IR.

Bei Resonanz erreicht die Admittanz der parallelen RLC-Schaltung einen Minimalwert. Daher,maximum voltage ist über jedes Element dieser Schaltung bei Resonanz vorhanden.

Strom fließt durch den Widerstand

Der durch den Widerstand fließende Strom ist

$$I_R = \frac{V}{R}$$

Ersetzen Sie den Wert von V in der obigen Gleichung.

$$I_R = \frac{IR}{R}$$

$$\Rightarrow I_R = I$$

deshalb, die current flowing through resistor bei Resonanz ist $\mathbf{\mathit{I_R = I}}$.

Strom fließt durch Induktivität

Der durch die Induktivität fließende Strom beträgt

$$I_L = \frac{V}{j X_L}$$

Ersetzen Sie den Wert von V in der obigen Gleichung.

$$I_L = \frac{IR}{j X_L}$$

$$\Rightarrow I_L = -j \lgroup \frac{R}{X_L} \rgroup I$$

$$\Rightarrow I_L = -jQI$$

deshalb, die current flowing through inductor at resonance is $I_L = -jQI$.

So, the magnitude of current flowing through inductor at resonance will be

$$|I_L| = QI$$

Where, Q is the Quality factor and its value is equal to $\frac{R}{X_L}$

Current flowing through Capacitor

The current flowing through capacitor is

$$I_C = \frac{V}{-j X_C}$$

Substitute the value of V in the above equation.

$$I_C = \frac{IR}{-j X_C}$$

$$\Rightarrow I_C = j \lgroup \frac{R}{X_C} \rgroup I$$

$$\Rightarrow I_C = jQI$$

Therefore, the current flowing through capacitor at resonance is $I_C = jQI$

So, the magnitude of current flowing through capacitor at resonance will be

$$|I_C| = QI$$

Where, Q is the Quality factor and its value is equal to $\frac{R}{X_C}$

Note − Parallel resonance RLC circuit is called as current magnification circuit. Because, the magnitude of current flowing through inductor and capacitor is equal to Q times the input sinusoidal current I.

An electric circuit is said to be a coupled circuit, when there exists a mutual inductance between the coils (or inductors) present in that circuit. Coil is nothing but the series combination of resistor and inductor. In the absence of resistor, coil becomes inductor. Sometimes, the terms coil and inductor are interchangeably used.

In this chapter, first let us discuss about the dot convention and then will discuss about classification of coupling.

Dot Convention

Dot convention is a technique, which gives the details about voltage polarity at the dotted terminal. This information is useful, while writing KVL equations.

• If the current enters at the dotted terminal of one coil (or inductor), then it induces a voltage at another coil (or inductor), which is having positive polarity at the dotted terminal.

• If the current leaves from the dotted terminal of one coil (or inductor), then it induces a voltage at another coil (or inductor), which is having negative polarity at the dotted terminal.

Classification of Coupling

We can classify coupling into the following two categories.

• Electrical Coupling
• Magnetic Coupling

Now, let us discuss about each type of coupling one by one.

Electrical Coupling

Electrical coupling occurs, when there exists a physical connection between two coils (or inductors). This coupling can be of either aiding type or opposing type. It is based on whether the current enters at the dotted terminal or leaves from the dotted terminal.

Coupling of Aiding type

Consider the following electric circuit, which is having two inductors that are connected in series.

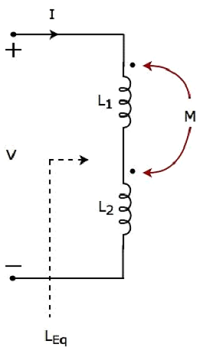
Since the two inductors are connected in series, the same current I flow through both inductors having self-inductances L₁ and L₂.

In this case, the current, I enter at the dotted terminal of each inductor. Hence, the induced voltage in each inductor will be having positive polarity at the dotted terminal due to the current flowing in another coil.

Apply KVL around the loop of the above electric circuit or network.

$$V - L_1 \frac{dI}{dt} - M \frac{dI}{dt} - L_2 \frac{dI}{dt} - M \frac{dI}{dt} = 0$$

$$V = L_1 \frac{dI}{dt} + L_2 \frac{dI}{dt} + 2M \frac{dI}{dt}$$

$$V = (L_1 + L_2 + 2M)\frac{dI}{dt}$$

The above equation is in the form of $\mathbf{\mathit{V = L_{Eq} \frac{dI}{dt}}}$

Therefore, the equivalent inductance of series combination of inductors shown in the above figure is

$$L_{Eq} = L_1 + L_2 + 2M$$

In this case, the equivalent inductance has been increased by 2M. Hence, the above electrical circuit is an example of electrical coupling which is of aiding type.

Coupling of Opposing type

Consider the following electric circuit, which is having two inductors that are connected in series.

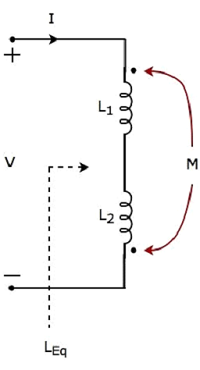
In the above circuit, the current I enters at the dotted terminal of the inductor having an inductance of L₁. Hence, it induces a voltage in the other inductor having an inductance of L₂. So, positive polarity of the induced voltage is present at the dotted terminal of this inductor.

In the above circuit, the current I leaves from the dotted terminal of the inductor having an inductance of L₂. Hence, it induces a voltage in the other inductor having an inductance of L₁. So, negative polarity of the induced voltage is present at the dotted terminal of this inductor.

Apply KVL around the loop of the above electric circuit or network.

$$V - L_1 \frac{dI}{dt} + M \frac{dI}{dt} - L_2 \frac{dI}{dt} + M \frac{dI}{dt} = 0$$

$$\Rightarrow V = L_1 \frac{dI}{dt} + L_2 \frac{dI}{dt} - 2M \frac{dI}{dt}$$

$$\Rightarrow V = (L_1 + L_2 - 2M)\frac{dI}{dt}$$

The above equation is in the form of $\mathbf{\mathit{V = L_{Eq} \frac{dI}{dt}}}$

Therefore, the equivalent inductance of series combination of inductors shown in the above figure is

$$L_{Eq} = L_1 + L_2 - 2M$$

In this case, the equivalent inductance has been decreased by 2M. Hence, the above electrical circuit is an example of electrical coupling which is of opposing type.

Magnetic Coupling

Magnetic coupling occurs, when there is no physical connection between two coils (or inductors). This coupling can be of either aiding type or opposing type. It is based on whether the current enters at the dotted terminal or leaves from the dotted terminal.

Coupling of Aiding type

Consider the following electrical equivalent circuit of transformer. It is having two coils and these are called as primary and secondary coils.

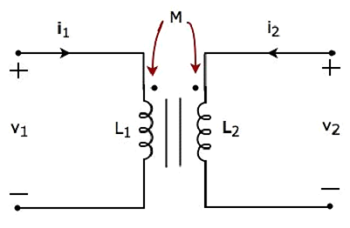
The currents flowing through primary and secondary coils are i₁ and i₂ respectively. In this case, these currents enter at the dotted terminal of respective coil. Hence, the induced voltage in each coil will be having positive polarity at the dotted terminal due to the current flowing in another coil.

Apply KVL around primary coil.

$$v_1 - L_1 \frac{d i_1}{dt} - M \frac{d i_2}{dt} = 0$$

$\Rightarrow v_1 = L_1 \frac{d i_1}{dt} + M \frac{d i_2}{dt}$Equation 1

Apply KVL around secondary coil.

$$v_2 - L_2 \frac{d i_2}{dt} - M \frac{d i_1}{dt} = 0$$

$\Rightarrow v_2 = L_2 \frac{d i_2}{dt} + M \frac{d i_1}{dt}$Equation 2

In Equation 1 and Equation 2, the self-induced voltage and mutually induced voltage have the same polarity. Hence, the above transformer circuit is an example of magnetic coupling, which is of aiding type.

Coupling of Opposing Type

Consider the following electrical equivalent circuit of transformer.

The currents flowing through primary and secondary coils are i₁ and i₂ respectively. In this case, the current, i₁ enters at the dotted terminal of primary coil. Hence, it induces a voltage in secondary coil. So, positive polarity of the induced voltage is present at the dotted terminal of this secondary coil.

In the above circuit, the current, i₂ leaves from the dotted terminal of secondary coil. Hence, it induces a voltage in primary coil. So, negative polarity of the induced voltage is present at the dotted terminal of this primary coil.

Apply KVL around primary coil.

$$v_1 - L_1 \frac{d i_1}{dt} + M \frac{d i_2}{dt} = 0$$

$\Rightarrow v_1 = L_1 \frac{d i_1}{dt} - M \frac{d i_2}{dt}$Equation 3

Apply KVL around secondary coil.

$$v_2 - L_2 \frac{d i_2}{dt} + M \frac{d i_1}{dt} = 0$$

$\Rightarrow v_2 = L_2 \frac{d i_2}{dt} - M \frac{d i_1}{dt}$Equation 4

In Equation 3 and Equation 4, self-induced voltage and mutually induced voltage are having opposite polarity. Hence, the above transformer circuit is an example of magnetic coupling, which is of opposing type.

In general, it is easy to analyze any electrical network, if it is represented with an equivalent model, which gives the relation between input and output variables. For this, we can use two port network representations. As the name suggests, two port networks contain two ports. Among which, one port is used as an input port and the other port is used as an output port. The first and second ports are called as port1 and port2 respectively.

One port network is a two terminal electrical network in which, current enters through one terminal and leaves through another terminal. Resistors, inductors and capacitors are the examples of one port network because each one has two terminals. One port network representation is shown in the following figure.

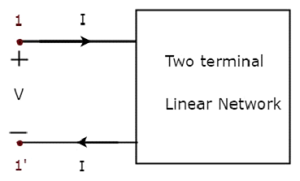
Here, the pair of terminals, 1 & 1’ represents a port. In this case, we are having only one port since it is a one port network.

Similarly, two port network is a pair of two terminal electrical network in which, current enters through one terminal and leaves through another terminal of each port. Two port network representation is shown in the following figure.

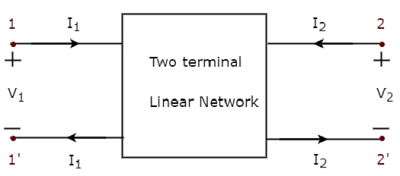
Here, one pair of terminals, 1 & 1’ represents one port, which is called as port1 and the other pair of terminals, 2 & 2’ represents another port, which is called as port2.

There are four variables V₁, V₂, I₁ and I₂ in a two port network as shown in the figure. Out of which, we can choose two variables as independent and another two variables as dependent. So, we will get six possible pairs of equations. These equations represent the dependent variables in terms of independent variables. The coefficients of independent variables are called as parameters. So, each pair of equations will give a set of four parameters.

Two Port Network Parameters

The parameters of a two port network are called as two port network parameters or simply, two port parameters. Following are the types of two port network parameters.

• Z parameters
• Y parameters
• T parameters
• T’ parameters
• h-parameters
• g-parameters

Now, let us discuss about these two port network parameters one by one.

Z parameters

We will get the following set of two equations by considering the variables V₁ & V₂ as dependent and I₁ & I₂ as independent. The coefficients of independent variables, I₁ and I₂ are called as Z parameters.

$$V_1 = Z_{11} I_1 + Z_{12} I_2$$

$$V_2 = Z_{21} I_1 + Z_{22} I_2$$

The Z parameters are

$$Z_{11} = \frac{V_1}{I_1}, \: when \: I_2 = 0$$

$$Z_{12} = \frac{V_1}{I_2}, \: when \: I_1 = 0$$

$$Z_{21} = \frac{V_2}{I_1}, \: when \: I_2 = 0$$

$$Z_{22} = \frac{V_2}{I_2}, \: when \: I_1 = 0$$

Z parameters are called as impedance parameters because these are simply the ratios of voltages and currents. Units of Z parameters are Ohm (Ω).

We can calculate two Z parameters, Z₁₁ and Z₂₁, by doing open circuit of port2. Similarly, we can calculate the other two Z parameters, Z₁₂ and Z₂₂ by doing open circuit of port1. Hence, the Z parameters are also called as open-circuit impedance parameters.

Y parameters

We will get the following set of two equations by considering the variables I₁ & I₂ as dependent and V₁ & V₂ as independent. The coefficients of independent variables, V₁ and V₂ are called as Y parameters.

$$I_1 = Y_{11} V_1 + Y_{12} V_2$$

$$I_2 = Y_{21} V_1 + Y_{22} V_2$$

The Y parameters are

$$Y_{11} = \frac{I_1}{V_1}, \: when \: V_2 = 0$$

$$Y_{12} = \frac{I_1}{V_2}, \: when \: V_1 = 0$$

$$Y_{21} = \frac{I_2}{V_1}, \: when \: V_2 = 0$$

$$Y_{22} = \frac{I_2}{V_2}, \: when \: V_1 = 0$$

Y parameters are called as admittance parameters because these are simply, the ratios of currents and voltages. Units of Y parameters are mho.

We can calculate two Y parameters, Y₁₁ and Y₂₁ by doing short circuit of port2. Similarly, we can calculate the other two Y parameters, Y₁₂ and Y₂₂ by doing short circuit of port1. Hence, the Y parameters are also called as short-circuit admittance parameters.

T parameters

We will get the following set of two equations by considering the variables V₁ & I₁ as dependent and V₂ & I₂ as independent. The coefficients of V₂ and -I₂ are called as T parameters.

$$V_1 = A V_2 - B I_2$$

$$I_1 = C V_2 - D I_2$$

The T parameters are

$$A = \frac{V_1}{V_2}, \: when \: I_2 = 0$$

$$B = -\frac{V_1}{I_2}, \: when \: V_2 = 0$$

$$C = \frac{I_1}{V_2}, \: when \: I_2 = 0$$

$$D = -\frac{I_1}{I_2}, \: when \: V_2 = 0$$

T parameters are called as transmission parameters or ABCD parameters. The parameters, A and D do not have any units, since those are dimension less. The units of parameters, B and C are ohm and mho respectively.

We can calculate two parameters, A and C by doing open circuit of port2. Similarly, we can calculate the other two parameters, B and D by doing short circuit of port2.

T ’ parameters

We will get the following set of two equations by considering the variables V₂ & I₂ as dependent and V₁ & I₁ as independent. The coefficients of V₁ and -I₁ are called as T’ parameters.

$$V_2 = A' V_1 - B' I_1$$

$$I_2 = C' V_1 - D' I_1$$

The T’ parameters are

$$A' = \frac{V_2}{V_1}, \: when\: I_1 = 0$$

$$B' = -\frac{V_2}{I_1}, \: when\: V_1 = 0$$

$$C' = \frac{I_2}{V_1}, \: when\: I_1 = 0$$

$$D' = -\frac{I_2}{I_1}, \: when \: V_1 = 0$$

T’ parameters are called as inverse transmission parameters or A’B’C’D’ parameters. The parameters A’ and D’ do not have any units, since those are dimension less. The units of parameters, B’ and C’, are Ohm and Mho respectively.

We can calculate two parameters, A’ and C’, by doing an open circuit of port1. Similarly, we can calculate the other two parameters, B’ and D’, by doing a short circuit of port1.

h-parameters

We will get the following set of two equations by considering the variables V₁ & I₂ as dependent and I₁ & V₂ as independent. The coefficients of independent variables, I₁ and V₂, are called as h-parameters.

$$V_1 = h_{11} I_1 + h_{12} V_2$$

$$I_2 = h_{21} I_1 + h_{22} V_2$$

The h-parameters are

$$h_{11} = \frac{V_1}{I_1},\: when\: V_2 = 0$$

$$h_{12} = \frac{V_1}{V_2},\: when\: I_1 = 0$$

$$h_{21} = \frac{I_2}{I_1},\: when\: V_2 = 0$$

$$h_{22} = \frac{I_2}{V_2},\: when\: I_1 = 0$$

h-parameters are called as hybrid parameters. The parameters, h₁₂ and h₂₁, do not have any units, since those are dimension-less. The units of parameters, h₁₁ and h₂₂, are Ohm and Mho respectively.

We can calculate two parameters, h₁₁ and h₂₁ by doing short circuit of port2. Similarly, we can calculate the other two parameters, h₁₂ and h₂₂ by doing open circuit of port1.

The h-parameters or hybrid parameters are useful in transistor modelling circuits (networks).

g-parameters

We will get the following set of two equations by considering the variables I₁ & V₂ as dependent and V₁ & I₂ as independent. The coefficients of independent variables, V₁ and I₂ are called as g-parameters.

$$I_1 = g_{11} V_1 + g_{12} I_2$$

$$V_2 = g_{21} V_1 + g_{22} I_2$$

The g-parameters are

$$g_{11} = \frac{I_1}{V_1},\: when\: I_2 = 0$$

$$g_{12} = \frac{I_1}{I_2},\: when\: V_1 = 0$$

$$g_{21} = \frac{V_2}{V_1},\: when\: I_2 = 0$$

$$g_{22} = \frac{V_2}{I_2},\: when \: V_1 = 0$$

g-parameters are called as inverse hybrid parameters. The parameters, g₁₂ and g₂₁ do not have any units, since those are dimension less. The units of parameters, g₁₁ and g₂₂ are mho and ohm respectively.

We can calculate two parameters, g₁₁ and g₂₁ by doing open circuit of port2. Similarly, we can calculate the other two parameters, g₁₂ and g₂₂ by doing short circuit of port1.

In the previous chapter, we discussed about six types of two-port network parameters. Now, let us convert one set of two-port network parameters into other set of two port network parameters. This conversion is known as two port network parameters conversion or simply, two-port parameters conversion.

Sometimes, it is easy to find one set of parameters of a given electrical network easily. In those situations, we can convert these parameters into the required set of parameters instead of calculating these parameters directly with more difficulty.

Now, let us discuss about some of the two port parameter conversions.

Procedure of two port parameter conversions

Follow these steps, while converting one set of two port network parameters into the other set of two port network parameters.

• Step 1 − Write the equations of a two port network in terms of desired parameters.

• Step 2 − Write the equations of a two port network in terms of given parameters.

• Step 3 − Re-arrange the equations of Step2 in such a way that they should be similar to the equations of Step1.

• Step 4 − By equating the similar equations of Step1 and Step3, we will get the desired parameters in terms of given parameters. We can represent these parameters in matrix form.

Z parameters to Y parameters

Here, we have to represent Y parameters in terms of Z parameters. So, in this case Y parameters are the desired parameters and Z parameters are the given parameters.

Step 1 − We know that the following set of two equations, which represents a two port network in terms of Y parameters.

$$I_1 = Y_{11} V_1 + Y_{12} V_2$$

$$I_2 = Y_{21} V_1 + Y_{22} V_2$$

We can represent the above two equations in matrix form as

$\begin{bmatrix}I_1 \\I_2 \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} \begin{bmatrix}V_1 \\V_2 \end{bmatrix}$Equation 1

Step 2 − We know that the following set of two equations, which represents a two port network in terms of Z parameters.

$$V_1 = Z_{11} I_1 + Z_{12} I_2$$

$$V_2 = Z_{21} I_1 + Z_{22} I_2$$

We can represent the above two equations in matrix form as

$$\begin{bmatrix}V_1 \\V_2 \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} \begin{bmatrix}I_1 \\I_2 \end{bmatrix}$$

Step 3 − We can modify it as

$\begin{bmatrix}I_1 \\I_2 \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix}^{-1} \begin{bmatrix}V_1 \\V_2 \end{bmatrix}$Equation 2

Step 4 − By equating Equation 1 and Equation 2, we will get

$$\begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix}^{-1} $$

$$\Rightarrow \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} = \frac{\begin{bmatrix}Z_{22} & -Z_{12} \\-Z_{21} & Z_{11} \end{bmatrix}}{\Delta Z}$$

Where,

$$\Delta Z = Z_{11} Z_{22} - Z_{12} Z_{21}$$

So, just by doing the inverse of Z parameters matrix, we will get Y parameters matrix.

Z parameters to T parameters

Here, we have to represent T parameters in terms of Z parameters. So, in this case T parameters are the desired parameters and Z parameters are the given parameters.

Step 1 − We know that, the following set of two equations, which represents a two port network in terms of T parameters.

$$V_1 = A V_2 - B I_2$$

$$I_1 = C V_2 - D I_2$$

Step 2 − We know that the following set of two equations, which represents a two port network in terms of Z parameters.

$$V_1 = Z_{11} I_1 + Z_{12} I_2$$

$$V_2 = Z_{21} I_1 + Z_{22} I_2$$

Step 3 − We can modify the above equation as

$$\Rightarrow V_2 - Z_{22} I_2 = Z_{21} I_1$$

$$\Rightarrow I_1 = \lgroup \frac{1}{Z_{21}} \rgroup V_2 - \lgroup \frac{Z_{22}}{Z_{21}} \rgroup I_2$$

Step 4 − The above equation is in the form of $I_1 = CV_2 − DI_2$. Here,

$$C = \frac{1}{Z_{21}}$$

$$D = \frac{Z_{22}}{Z_{21}}$$

Step 5 − Substitute $I_1$ value of Step 3 in $V_1$ equation of Step 2.

$$V_1 = Z_{11} \lbrace \lgroup \frac {1}{Z_{12}} \rgroup V_2 - \lgroup \frac {Z_{22}}{Z_{21}} \rgroup I_2 \rbrace + Z_{12} I_2$$

$$\Rightarrow V_1 = \lgroup \frac {Z_{11}}{Z_{21}} \rgroup V_2 - \lgroup \frac{Z_{11} Z_{22} - Z_{12} Z_{21}}{Z_{21}} \rgroup I_2$$

Step 6 − The above equation is in the form of $V_1 = AV_2 − BI_2$. Here,

$$A = \frac{Z_{11}}{Z_{21}}$$

$$B = \frac{Z_{11} Z_{22} - Z_{12} Z_{21}}{Z_{21}}$$

Step 7 − Therefore, the T parameters matrix is

$$\begin{bmatrix}A & B \\C & D \end{bmatrix} = \begin{bmatrix}\frac{Z_{11}}{Z_{21}} & \frac{Z_{11}Z_{22} - Z_{12}Z_{21}}{Z_{21}} \\\frac{1}{Z_{21}} & \frac{Z_{22}}{Z_{21}} \end{bmatrix}$$

Y parameters to Z parameters

Here, we have to represent Z parameters in terms of Y parameters. So, in this case Z parameters are the desired parameters and Y parameters are the given parameters.

Step 1 − We know that, the following matrix equation of two port network regarding Z parameters as

$\begin{bmatrix}V_1 \\V_2 \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} \begin{bmatrix}I_1 \\I_2 \end{bmatrix}$Equation 3

Step 2 - Wir wissen, dass die folgende Matrixgleichung eines Zwei-Port-Netzwerks bezüglich Y-Parametern als

$$\begin{bmatrix}I_1 \\I_2 \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} \begin{bmatrix}V_1 \\V_2 \end{bmatrix}$$

Step 3 - Wir können es ändern als

$\begin{bmatrix}V_1 \\V_2 \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix}^{-1} \begin{bmatrix}I_1 \\I_2 \end{bmatrix}$Equation 4

Step 4 - Durch Gleichsetzen von Gleichung 3 und Gleichung 4 erhalten wir

$$\begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix}^{-1}$$

$$\Rightarrow \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} = \frac{\begin{bmatrix}Y_{22} & - Y_{12} \\- Y_{21} & Y_{11} \end{bmatrix}}{\Delta Y}$$

Wo,

$$\Delta Y = Y_{11} Y_{22} - Y_{12} Y_{21}$$

Also, einfach indem du das machst inverse of Y parameters matrixerhalten wir die Z-Parametermatrix.

Y-Parameter zu T-Parametern

Hier müssen wir T-Parameter als Y-Parameter darstellen. In diesem Fall sind also T-Parameter die gewünschten Parameter und Y-Parameter die angegebenen Parameter.

Step 1 - Wir wissen, dass der folgende Satz von zwei Gleichungen, die ein Zwei-Port-Netzwerk in Bezug auf darstellt T parameters.

$$V_1 = A V_2 - B I_2$$

$$I_1 = C V_2 - D I_2$$

Step 2 - Wir wissen, dass der folgende Satz von zwei Gleichungen eines Zwei-Port-Netzwerks in Bezug auf Y-Parameter.

$$I_1 = Y_{11} V_1 + Y_{12} V_2$$

$$I_2 = Y_{21} V_1 + Y_{22} V_2$$

Step 3 - Wir können die obige Gleichung als ändern

$$\Rightarrow I_2 - Y_{22} V_2 = Y_{21} V_1$$

$$\Rightarrow V_1 = \lgroup \frac{- Y_{22}}{Y_{21}} \rgroup V_2 - \lgroup \frac{-1}{Y_{21}} \rgroup I_2$$

Step 4 - Die obige Gleichung hat die Form von $V_1 = AV_2 − BI_2$. Hier,

$$A = \frac{- Y_{22}}{Y_{21}}$$

$$B = \frac{-1}{Y_{21}}$$

Step 5 - Ersatz $V_1$ Wert von Schritt 3 in $I_1$ Gleichung von Schritt 2.

$$I_1 = Y_{11} \lbrace \lgroup \frac{- Y_{22}}{Y_{21}} \rgroup V_2 - \lgroup \frac{-1}{Y_{21}} \rgroup I_2 \rbrace + Y_{12} V_2$$

$$\Rightarrow I_1 = \lgroup \frac {Y_{12} Y_{21} - Y_{11} Y_{22}}{Y_{21}} \rgroup V_2 - \lgroup \frac{- Y_{11}} {Y_{21}} \rgroup I_2$$

Step 6 - Die obige Gleichung hat die Form von $I_1 = CV_2 − DI_2$. Hier,

$$C = \frac {Y_{12} Y_{21} - Y_{11} Y_{22}}{Y_{21}}$$

$$D = \frac{- Y_{11}} {Y_{21}}$$

Step 7 - Deshalb die T parameters matrix ist

$$\begin{bmatrix}A & B \\C & D \end{bmatrix} = \begin{bmatrix}\frac{-Y_{22}}{Y_{21}} & \frac{-1}{Y_{21}} \\\frac{Y_{12}Y_{21} - Y_{11}Y_{22}}{Y_{21}} & \frac{-Y_{11}}{Y_{21}} \end{bmatrix}$$

T-Parameter zu h-Parametern

Hier müssen wir h-Parameter in Form von T-Parametern darstellen. In diesem Fall sind also h-Parameter die gewünschten Parameter und T-Parameter die gegebenen Parameter.

Step 1 - Wir wissen das, das Folgende h-parameters eines Zwei-Port-Netzwerks.

$$h_{11} = \frac{V_1}{I_1}, \: when \: V_2 = 0$$

$$h_{12} = \frac{V_1}{V_2}, \: when \: I_1 = 0$$

$$h_{21} = \frac{I_2}{I_1}, \: when \: V_2 = 0$$

$$h_{22} = \frac{I_2}{V_2}, \: when \: I_1 = 0$$

Step 2 - Wir wissen, dass der folgende Satz von zwei Gleichungen von zwei Port-Netzwerk in Bezug auf T parameters.

$V_1 = A V_2 - B I_2$Equation 5

$I_1 = C V_2 - D I_2$Equation 6

Step 3 - Ersatz $V_2 = 0$ in den obigen Gleichungen, um die zwei h-Parameter zu finden, $h_{11}$ und $h_{21}$.

$$\Rightarrow V_1 = -B I_2$$

$$\Rightarrow I_1 = -D I_2$$

Ersatz, $V_1$ und $I_1$ Werte in h-Parameter, $h_{11}$.

$$h_{11} = \frac{-B I_2}{-D I_2}$$

$$\Rightarrow h_{11} = \frac{B}{D}$$

Ersatz $I_1$ Wert im h-Parameter $h_{21}$.

$$h_{21} = \frac{I_2}{- D I_2}$$

$$\Rightarrow h_{21} = - \frac{1}{D}$$

Step 4 - Ersatz $I_1 = 0$ in der zweiten Gleichung von Schritt 2, um den h-Parameter zu finden $h_{22}$.

$$0 = C V_2 - D I_2$$

$$\Rightarrow C V_2 = D I_2$$

$$\Rightarrow \frac{I_2}{V_2} = \frac{C}{D}$$

$$\Rightarrow h_{22} = \frac{C}{D}$$

Step 5 - Ersatz $I_2 = \lgroup \frac{C}{D} \rgroup V_2$ in der ersten Gleichung von Schritt 2, um den h-Parameter zu finden, $h_{12}$.

$$V_1 = A V_2 - B \lgroup \frac{C}{D} \rgroup V_2$$

$$\Rightarrow V_1 = \lgroup \frac{AD - BC}{D} \rgroup V_2$$

$$\Rightarrow \frac{V_1}{V_2} = \frac{AD - BC}{D}$$

$$\Rightarrow h_{12} = \frac{AD - BC}{D}$$

Step 6 - Daher ist die h-Parameter-Matrix

$$\begin{bmatrix}h_{11} & h_{12} \\h_{21} & h_{22} \end{bmatrix} = \begin{bmatrix}\frac{B}{D} & \frac{AD - BC}{D} \\-\frac{1}{D} & \frac{C}{D} \end{bmatrix}$$

h-Parameter bis Z-Parameter

Hier müssen wir Z-Parameter als h-Parameter darstellen. In diesem Fall sind also Z-Parameter die gewünschten Parameter und h-Parameter die gegebenen Parameter.

Step 1 - Wir wissen, dass der folgende Satz von zwei Gleichungen von zwei Port-Netzwerk in Bezug auf Z parameters.

$$V_1 = Z_{11} I_1 + Z_{12} I_2$$

$$V_2 = Z_{21} I_1 + Z_{22} I_2$$

Step 2 - Wir wissen, dass der folgende Satz von zwei Gleichungen des Zwei-Port-Netzwerks in Bezug auf h-parameters.

$$V_1 = h_{11} I_1 + h_{12} V_2$$

$$I_2 = h_{21} I_1 + h_{22} V_2$$

Step 3 - Wir können die obige Gleichung als ändern

$$\Rightarrow I_2 - h_{21} I_1 = h_{22} V_2$$

$$\Rightarrow V_2 = \frac{I_2 - h_{21} I_1}{h_{22}}$$

$$\Rightarrow V_2 = \lgroup \frac{-h_{21}}{h_{22}} \rgroup I_1 + \lgroup \frac{1}{h_{22}} \rgroup I_2$$

Die obige Gleichung hat die Form von $V_2 = Z_{21} I_1 + Z_{22} I_2. Here,$

$$Z_{21} = \frac{-h_{21}}{h_{22}}$$

$$Z_{22} = \frac{1}{h_{22}}$$

Step 4- Ersetzen Sie den V ₂ -Wert in der ersten Gleichung von Schritt 2.

$$V_1 = h_{11} I_1 + h_{21} \lbrace \lgroup \frac{-h_{21}}{h_{22}} \rgroup I_1 + \lgroup \frac{1}{h_{22}} \rgroup I_2 \rbrace$$

$$\Rightarrow V_1 = \lgroup \frac{h_{11}h_{22} - h_{12}h_{21}}{h_{22}} \rgroup I_1 + \lgroup \frac{h_{12}}{h_{22}} \rgroup I_2$$

Die obige Gleichung hat die Form von $V_1 = Z_{11}I_1 + Z_{12}I_2$. Hier,

$$Z_{11} = \frac{h_{11}h_{22} - h_{12}h_{21}}{h_{22}}$$

$$Z_{12} = \frac{h_{12}}{h_{22}}$$

Step 5 - Daher ist die Z-Parametermatrix

$$\begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} = \begin{bmatrix}\frac{h_{11}h_{22} - h_{12}h_{21}}{h_{22}} & \frac{h_{12}}{h_{22}} \\\frac{-h_{21}}{h_{22}} & \frac{1}{h_{22}} \end{bmatrix}$$

Auf diese Weise können wir einen Parametersatz in einen anderen Parametersatz konvertieren.

Filter filtern, wie der Name schon sagt, die Frequenzkomponenten. Das heißt, sie erlauben bestimmte Frequenzkomponenten und / oder lehnen einige andere Frequenzkomponenten ab.

Lassen Sie uns in diesem Kapitel über die passive filters. Dies sind die elektrischen Schaltkreise oder Netzwerke mit passiven Elementen wie Widerstand, Induktivität und Kondensator.

Arten von Filtern

Filter werden hauptsächlich in klassifiziert four typesbasierend auf dem Frequenzband, das zulässt, und / oder dem Frequenzband, das ablehnt. Im Folgenden sind die Filtertypen aufgeführt.

• Tiefpassfilter
• Hochpassfilter
• Bandpassfilter
• Bandstoppfilter

Tiefpassfilter

Tiefpassfilter, wie der Name schon sagt, erlaubt nur (Durchgänge) low frequencyKomponenten. Das heißt, es werden alle anderen Hochfrequenzkomponenten zurückgewiesen (blockiert).

Die S-Domain circuit diagram (Netzwerk) des Tiefpassfilters ist in der folgenden Abbildung dargestellt.

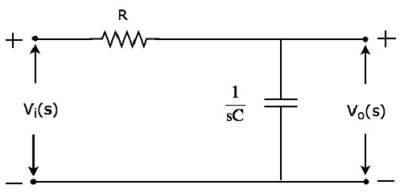
Es besteht aus zwei passiven Elementen Widerstand und Kondensator, die miteinander verbunden sind series. Die Eingangsspannung wird über diese gesamte Kombination angelegt und der Ausgang wird als Spannung über dem Kondensator betrachtet.

Hier, $V_i(s)$ und $V_o(s)$ sind die Laplace-Transformationen der Eingangsspannung, $v_i(t)$ und Ausgangsspannung, $v_o(t)$ beziehungsweise.

Das transfer function des oben genannten Netzwerks ist

$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{\frac{1}{sC}}{R + \frac{1}{sC}}$$

$$\Rightarrow H(s) = \frac{1}{1 + sCR}$$

Ersatz, $s = j \omega$ in der obigen Gleichung.

$$H(j \omega) = \frac{1}{1 + j \omega CR}$$

Größe der Übertragungsfunktion ist

$$|H(j \omega)| = \frac{1}{\sqrt{(1 + (\omega CR)^2}}$$

• Bei ω = 0 ist die Größe der Übertragungsfunktion gleich 1.

• Beim $\omega = \frac{1}{CR}$ist die Größe der Übertragungsfunktion gleich 0,707.

• Bei ω = ∞ ist die Größe der Übertragungsfunktion gleich 0.

Daher ist die Größe der Übertragungsfunktion von Low pass filtervariiert von 1 bis 0, da ω von 0 bis ∞ variiert.

Hochpassfilter

Hochpassfilter, wie der Name schon sagt, erlaubt nur (Durchgänge) high frequencyKomponenten. Das heißt, es werden alle Niederfrequenzkomponenten zurückgewiesen (blockiert).

Die S-Domain circuit diagram (Netzwerk) des Hochpassfilters ist in der folgenden Abbildung dargestellt.

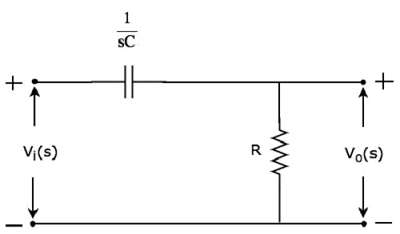
Es besteht aus zwei passiven Elementen Kondensator und Widerstand, die miteinander verbunden sind series. Die Eingangsspannung wird über diese gesamte Kombination angelegt und der Ausgang wird als Spannung über dem Widerstand betrachtet.

Hier, $V_i(s)$ und $V_o(s)$ sind die Laplace-Transformationen der Eingangsspannung, $v_i(t)$ und Ausgangsspannung, $v_o(t)$ beziehungsweise.

Das transfer function des oben genannten Netzwerks ist

$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{R}{R + \frac{1}{sC}}$$

$$\Rightarrow H(s) = \frac{sCR}{1 + sCR}$$

Ersatz, $s = j \omega$ in der obigen Gleichung.

$$H(j \omega) = \frac{j \omega CR}{1 + j \omega CR}$$

Größe der Übertragungsfunktion ist

$$|H(j \omega)| = \frac{\omega CR}{\sqrt{(1 + (\omega CR)^2}}$$

• Bei ω = 0 ist die Größe der Übertragungsfunktion gleich 0.

• Beim $\omega = \frac{1}{CR}$ist die Größe der Übertragungsfunktion gleich 0,707.

• Bei ω = ∞ ist die Größe der Übertragungsfunktion gleich 1.

Daher ist die Größe der Übertragungsfunktion von High pass filtervariiert von 0 bis 1, da ω von 0 bis ∞ variiert.

Bandpassfilter

Bandpassfilter, wie der Name schon sagt allows (geht vorbei) nur one bandvon Frequenzen. Im Allgemeinen liegt dieses Frequenzband zwischen dem Niederfrequenzbereich und dem Hochfrequenzbereich. Das heißt, dieser Filter weist sowohl Nieder- als auch Hochfrequenzkomponenten zurück (blockiert sie).

Die S-Domain circuit diagram (Netzwerk) des Bandpassfilters ist in der folgenden Abbildung dargestellt.

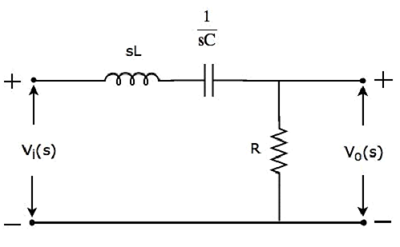
Es besteht aus drei passiven Elementen Induktivität, Kondensator und Widerstand, die miteinander verbunden sind series. Die Eingangsspannung wird über diese gesamte Kombination angelegt und der Ausgang wird als Spannung über dem Widerstand betrachtet.

Hier, $V_i(s)$ und $V_o(s)$ sind die Laplace-Transformationen der Eingangsspannung, $v_i(t)$ und Ausgangsspannung, $v_o(t)$ beziehungsweise.

Das transfer function des oben genannten Netzwerks ist

$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{R}{R + \frac{1}{sC} + sL}$$

$$\Rightarrow H(s) = \frac{s CR}{s^2 LC + sCR + 1}$$

Ersatz $s = j \omega$ in der obigen Gleichung.

$$H(j \omega) = \frac{j \omega CR}{1 - \omega^2 LC + j \omega CR}$$

Größe der Übertragungsfunktion ist

$$|H(j \omega)| = \frac{\omega CR}{\sqrt{(1 - \omega^2 LC)^2 + (\omega CR)^2}}$$

• Bei ω = 0 ist die Größe der Übertragungsfunktion gleich 0.

• Beim $\omega = \frac{1}{\sqrt{LC}}$ist die Größe der Übertragungsfunktion gleich 1.

• Bei ω = ∞ ist die Größe der Übertragungsfunktion gleich 0.

Daher ist die Größe der Übertragungsfunktion von Band pass filtervariiert von 0 bis 1 & 1 bis 0, da ω von 0 bis ∞ variiert.

Bandstoppfilter

Bandstoppfilter, wie der Name schon sagt, lehnt nur ein Frequenzband ab (blockiert es). Im Allgemeinen liegt dieses Frequenzband zwischen dem Niederfrequenzbereich und dem Hochfrequenzbereich. Das heißt, dieser Filter erlaubt (durchläuft) sowohl Nieder- als auch Hochfrequenzkomponenten.

Die S-Domain (Netzwerk) von circuit diagramund Stoppfilter ist in der folgenden Abbildung dargestellt.

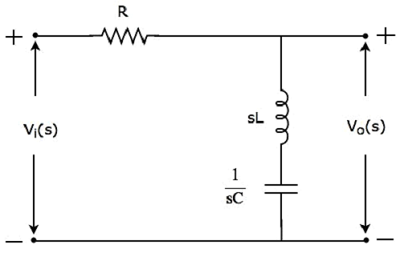
Es besteht aus drei passiven Elementen Widerstand, Induktivität und Kondensator, die miteinander verbunden sind series. Die Eingangsspannung wird über diese gesamte Kombination angelegt und der Ausgang wird als die Spannung über der Kombination von Induktor und Kondensator betrachtet.

Hier, $V_i(s)$ und $V_o(s)$ sind die Laplace-Transformationen der Eingangsspannung, $v_i(t)$ und Ausgangsspannung, $v_o(t)$ beziehungsweise.

Das transfer function des oben genannten Netzwerks ist

$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{sL + \frac{1}{sC}}{R + sL + \frac{1}{sC}}$$

$$\Rightarrow H(s) = \frac{s^2 LC + 1}{s^2 LC + sCR + 1}$$

Ersatz, $s = j \omega$ in der obigen Gleichung.

$$H(j \omega) = \frac{1 - \omega^2 LC}{1 - \omega^2 LC + j \omega CR}$$

Größe der Übertragungsfunktion ist

$$|H(j \omega)| = \frac{1 - \omega^2 LC}{\sqrt{(1 - \omega^2 LC)^2 + (\omega CR)^2}}$$

• Bei ω = 0 ist die Größe der Übertragungsfunktion gleich 1.

• Beim $\omega = \frac{1}{\sqrt{LC}}$ist die Größe der Übertragungsfunktion gleich 0.

• Bei ω = ∞ ist die Größe der Übertragungsfunktion gleich 1.

Daher ist die Größe der Übertragungsfunktion von Band stop filtervariiert von 1 bis 0 und 0 bis 1, da ω von 0 bis ∞ variiert.