Netzwerktheorie - Zwei-Port-Netzwerke
Im Allgemeinen ist es einfach, ein elektrisches Netzwerk zu analysieren, wenn es mit einem äquivalenten Modell dargestellt wird, das die Beziehung zwischen Eingangs- und Ausgangsvariablen angibt. Dafür können wir verwendentwo port networkDarstellungen. Wie der Name schon sagt, enthalten zwei Portnetzwerke zwei Ports. Unter diesen wird ein Port als Eingabeport und der andere Port als Ausgabeport verwendet. Der erste und der zweite Port werden als Port1 bzw. Port2 bezeichnet.
One port networkist ein elektrisches Netzwerk mit zwei Anschlüssen, in dem Strom durch einen Anschluss eintritt und durch einen anderen Anschluss austritt. Widerstände, Induktivitäten und Kondensatoren sind Beispiele für ein Port-Netzwerk, da jedes über zwei Anschlüsse verfügt. Eine Port-Netzwerkdarstellung ist in der folgenden Abbildung dargestellt.
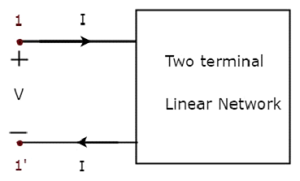
Hier repräsentiert das Terminalpaar 1 & 1 'einen Port. In diesem Fall haben wir nur einen Port, da es sich um ein Netzwerk mit einem Port handelt.
Ähnlich, two port networkist ein Paar von zwei elektrischen Anschlüssen, in denen Strom durch einen Anschluss eintritt und durch einen anderen Anschluss jedes Ports austritt. Die Darstellung des Netzwerks mit zwei Ports ist in der folgenden Abbildung dargestellt.
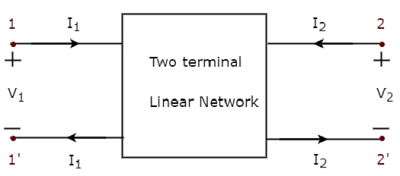
Hier repräsentiert ein Terminalpaar 1 & 1 'einen Port, der als bezeichnet wird port1 und das andere Paar von Anschlüssen, 2 & 2 ', repräsentiert einen anderen Port, der als bezeichnet wird port2.
Es gibt four variablesV 1 , V 2 , I 1 und I 2 in einem Zwei-Port-Netzwerk, wie in der Abbildung gezeigt. Aus diesen können wir zwei Variablen als unabhängig und zwei weitere Variablen als abhängig auswählen. Wir erhalten also sechs mögliche Gleichungspaare. Diese Gleichungen repräsentieren die abhängigen Variablen als unabhängige Variablen. Die Koeffizienten unabhängiger Variablen werden als bezeichnetparameters. Jedes Gleichungspaar ergibt also einen Satz von vier Parametern.
Zwei Port-Netzwerkparameter
Die Parameter eines Zwei-Port-Netzwerks werden als bezeichnet two port network parametersoder einfach zwei Portparameter. Im Folgenden sind die Typen von zwei Port-Netzwerkparametern aufgeführt.
- Z-Parameter
- Y-Parameter
- T-Parameter
- T 'Parameter
- h-parameters
- g-parameters
Lassen Sie uns nun nacheinander über diese beiden Port-Netzwerkparameter sprechen.
Z-Parameter
Wir erhalten den folgenden Satz von zwei Gleichungen, indem wir die Variablen V 1 & V 2 als abhängig und I 1 & I 2 als unabhängig betrachten. Die Koeffizienten der unabhängigen Variablen I 1 und I 2 werden als bezeichnetZ parameters.
$$ V_1 = Z_ {11} I_1 + Z_ {12} I_2 $$
$$ V_2 = Z_ {21} I_1 + Z_ {22} I_2 $$
Das Z parameters sind
$$ Z_ {11} = \ frac {V_1} {I_1}, \: wenn \: I_2 = 0 $$
$$ Z_ {12} = \ frac {V_1} {I_2}, \: wenn \: I_1 = 0 $$
$$ Z_ {21} = \ frac {V_2} {I_1}, \: wenn \: I_2 = 0 $$
$$ Z_ {22} = \ frac {V_2} {I_2}, \: wenn \: I_1 = 0 $$
Z-Parameter heißen als impedance parametersdenn dies sind einfach die Verhältnisse von Spannungen und Strömen. Einheiten der Z-Parameter sind Ohm (Ω).
Wir können zwei Z-Parameter, Z 11 und Z 21 , berechnen , indem wir den offenen Stromkreis von Port 2 ausführen. In ähnlicher Weise können wir die beiden anderen Z-Parameter Z 12 und Z 22 berechnen, indem wir den offenen Stromkreis von Port 1 ausführen. Daher werden die Z-Parameter auch als bezeichnetopen-circuit impedance parameters.
Y-Parameter
Wir erhalten den folgenden Satz von zwei Gleichungen, indem wir die Variablen I 1 & I 2 als abhängig und V 1 & V 2 als unabhängig betrachten. Die Koeffizienten der unabhängigen Variablen V 1 und V 2 werden als bezeichnetY parameters.
$$ I_1 = Y_ {11} V_1 + Y_ {12} V_2 $$
$$ I_2 = Y_ {21} V_1 + Y_ {22} V_2 $$
Das Y parameters sind
$$ Y_ {11} = \ frac {I_1} {V_1}, \: wenn \: V_2 = 0 $$
$$ Y_ {12} = \ frac {I_1} {V_2}, \: wenn \: V_1 = 0 $$
$$ Y_ {21} = \ frac {I_2} {V_1}, \: wenn \: V_2 = 0 $$
$$ Y_ {22} = \ frac {I_2} {V_2}, \: wenn \: V_1 = 0 $$
Y-Parameter werden als bezeichnet admittance parametersdenn dies sind einfach die Verhältnisse von Strömen und Spannungen. Einheiten von Y-Parametern sind mho.
Wir können zwei Y-Parameter, Y 11 und Y 21, berechnen, indem wir Port 2 kurzschließen. In ähnlicher Weise können wir die beiden anderen Y-Parameter Y 12 und Y 22 berechnen, indem wir Port 1 kurzschließen. Daher werden die Y-Parameter auch als bezeichnetshort-circuit admittance parameters.
T-Parameter
Wir erhalten den folgenden Satz von zwei Gleichungen, indem wir die Variablen V 1 & I 1 als abhängig und V 2 & I 2 als unabhängig betrachten. Die Koeffizienten von V 2 und -I 2 werden als bezeichnetT parameters.
$$ V_1 = A V_2 - B I_2 $$
$$ I_1 = C V_2 - D I_2 $$
Das T parameters sind
$$ A = \ frac {V_1} {V_2}, \: wenn \: I_2 = 0 $$
$$ B = - \ frac {V_1} {I_2}, \: wenn \: V_2 = 0 $$
$$ C = \ frac {I_1} {V_2}, \: wenn \: I_2 = 0 $$
$$ D = - \ frac {I_1} {I_2}, \: wenn \: V_2 = 0 $$
T-Parameter werden als Übertragungsparameter oder bezeichnet ABCD parameters. Die Parameter A und D haben keine Einheiten, da diese dimensionslos sind. Die Einheiten der Parameter B und C sind Ohm bzw. mho.
Wir können zwei Parameter, A und C, berechnen, indem wir den offenen Stromkreis von Port2 ausführen. In ähnlicher Weise können wir die beiden anderen Parameter B und D berechnen, indem wir Port 2 kurzschließen.
T 'Parameter
Wir erhalten den folgenden Satz von zwei Gleichungen, indem wir die Variablen V 2 & I 2 als abhängig und V 1 & I 1 als unabhängig betrachten. Die Koeffizienten von V 1 und -I 1 werden als bezeichnetT’ parameters.
$$ V_2 = A 'V_1 - B' I_1 $$
$$ I_2 = C 'V_1 - D' I_1 $$
Das T’ parameters sind
$$ A '= \ frac {V_2} {V_1}, \: wenn \: I_1 = 0 $$
$$ B '= - \ frac {V_2} {I_1}, \: wenn \: V_1 = 0 $$
$$ C '= \ frac {I_2} {V_1}, \: wenn \: I_1 = 0 $$
$$ D '= - \ frac {I_2} {I_1}, \: wenn \: V_1 = 0 $$
T'-Parameter werden als inverse Übertragungsparameter oder bezeichnet A’B’C’D’ parameters. Die Parameter A 'und D' haben keine Einheiten, da diese dimensionslos sind. Die Einheiten der Parameter B 'und C' sind Ohm bzw. Mho.
Wir können zwei Parameter, A 'und C', berechnen, indem wir einen offenen Stromkreis von Port1 ausführen. In ähnlicher Weise können wir die beiden anderen Parameter B 'und D' berechnen, indem wir einen Kurzschluss von Port1 durchführen.
h-Parameter
Wir erhalten den folgenden Satz von zwei Gleichungen, indem wir die Variablen V 1 & I 2 als abhängig und I 1 & V 2 als unabhängig betrachten. Die Koeffizienten unabhängiger Variablen I 1 und V 2 werden als bezeichneth-parameters.
$$ V_1 = h_ {11} I_1 + h_ {12} V_2 $$
$$ I_2 = h_ {21} I_1 + h_ {22} V_2 $$
Die h-Parameter sind
$$ h_ {11} = \ frac {V_1} {I_1}, \: wenn \: V_2 = 0 $$
$$ h_ {12} = \ frac {V_1} {V_2}, \: wenn \: I_1 = 0 $$
$$ h_ {21} = \ frac {I_2} {I_1}, \: wenn \: V_2 = 0 $$
$$ h_ {22} = \ frac {I_2} {V_2}, \: wenn \: I_1 = 0 $$
h-Parameter heißen als hybrid parameters. Die Parameter h 12 und h 21 haben keine Einheiten, da diese dimensionslos sind. Die Einheiten der Parameter h 11 und h 22 sind Ohm bzw. Mho.
Wir können zwei Parameter berechnen, h 11 und h 21, indem wir Port 2 kurzschließen. In ähnlicher Weise können wir die beiden anderen Parameter h 12 und h 22 berechnen, indem wir den offenen Stromkreis von Port 1 ausführen.
Die h-Parameter oder Hybridparameter sind in Transistormodellierungsschaltungen (Netzwerken) nützlich.
g-Parameter
Wir erhalten den folgenden Satz von zwei Gleichungen, indem wir die Variablen I 1 & V 2 als abhängig und V 1 & I 2 als unabhängig betrachten. Die Koeffizienten der unabhängigen Variablen V 1 und I 2 werden als bezeichnetg-parameters.
$$ I_1 = g_ {11} V_1 + g_ {12} I_2 $$
$$ V_2 = g_ {21} V_1 + g_ {22} I_2 $$
Das g-parameters sind
$$ g_ {11} = \ frac {I_1} {V_1}, \: wenn \: I_2 = 0 $$
$$ g_ {12} = \ frac {I_1} {I_2}, \: wenn \: V_1 = 0 $$
$$ g_ {21} = \ frac {V_2} {V_1}, \: wenn \: I_2 = 0 $$
$$ g_ {22} = \ frac {V_2} {I_2}, \: wenn \: V_1 = 0 $$
g-Parameter heißen als inverse hybrid parameters. Die Parameter g 12 und g 21 haben keine Einheiten, da diese dimensionslos sind. Die Einheiten der Parameter g 11 und g 22 sind mho bzw. Ohm.
Wir können zwei Parameter berechnen, g 11 und g 21, indem wir den offenen Stromkreis von Port 2 ausführen. In ähnlicher Weise können wir die beiden anderen Parameter g 12 und g 22 berechnen, indem wir Port 1 kurzschließen.