Netzwerktheorie - Überlagerungssatz

Superposition theorembasiert auf dem Konzept der Linearität zwischen der Reaktion und Erregung eines Stromkreises. Es heißt, dass die Antwort in einem bestimmten Zweig einer linearen Schaltung, wenn mehrere unabhängige Quellen gleichzeitig wirken, äquivalent zu der Summe der Antworten ist, die aufgrund jeder unabhängigen Quelle gleichzeitig wirken.

Bei dieser Methode werden wir nur berücksichtigen one independent sourcezu einer Zeit. Wir müssen also die verbleibenden unabhängigen Quellen aus der Schaltung entfernen. Wir können die Spannungsquellen beseitigen, indem wir ihre beiden Klemmen kurzschließen, und in ähnlicher Weise die Stromquellen, indem wir ihre beiden Klemmen öffnen.

Daher müssen wir die Antwort in einem bestimmten Zweig finden ‘n’ timeswenn es 'n' unabhängige Quellen gibt. Die Antwort in einem bestimmten Zweig könnte entweder Strom sein, der durch diesen Zweig fließt, oder Spannung über diesen Zweig.

Verfahren des Überlagerungssatzes

Befolgen Sie diese Schritte, um die Antwort in einem bestimmten Zweig mithilfe des Überlagerungssatzes zu finden.

Step 1 - Finden Sie die Antwort in einem bestimmten Zweig, indem Sie eine unabhängige Quelle berücksichtigen und die verbleibenden unabhängigen Quellen im Netzwerk eliminieren.

Step 2 - Wiederholen Sie Schritt 1 für alle unabhängigen Quellen im Netzwerk.

Step 3 - Fügen Sie alle Antworten hinzu, um die Gesamtantwort in einem bestimmten Zweig zu erhalten, wenn alle unabhängigen Quellen im Netzwerk vorhanden sind.

Beispiel

Finden Sie den Strom, der durch den 20 Ω-Widerstand der folgenden Schaltung fließt, mit superposition theorem.

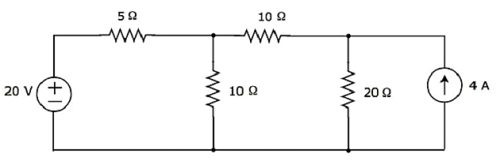
Step 1 - Lassen Sie uns den Strom, der durch den 20 Ω-Widerstand fließt, nur unter Berücksichtigung betrachten 20 V voltage source. In diesem Fall können wir die 4-A-Stromquelle eliminieren, indem wir sie offenlegen. Das modifizierte Schaltbild ist in der folgenden Abbildung dargestellt.

Es gibt nur einen Hauptknoten außer Masse in der obigen Schaltung. Also können wir verwendennodal analysisMethode. Die Knotenspannung V ₁ ist in der folgenden Abbildung gekennzeichnet. Hier ist V ₁ die Spannung von Knoten 1 in Bezug auf Masse.

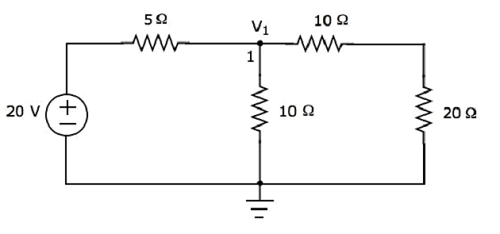
Das nodal equation am Knoten 1 ist

$$ \ frac {V_1 - 20} {5} + \ frac {V_1} {10} + \ frac {V_1} {10 + 20} = 0 $$

$$ \ Rightarrow \ frac {6V_1 - 120 + 3V_1 + V_1} {30} = 0 $$

$$ \ Rightarrow 10V_1 = 120 $$

$$ \ Rightarrow V_1 = 12V $$

Das current flowing through 20 Ω resistor kann durch die folgende Vereinfachung gefunden werden.

$$ I_1 = \ frac {V_1} {10 + 20} $$

Ersetzen Sie den Wert von V ₁ in der obigen Gleichung.

$$ I_1 = \ frac {12} {10 + 20} = \ frac {12} {30} = 0,4 A $$

Daher ist der durch den 20 Ω Widerstand fließende Strom 0.4 Awenn nur eine 20 V Spannungsquelle berücksichtigt wird.

Step 2 - Lassen Sie uns den Strom, der durch den 20 Ω-Widerstand fließt, nur unter Berücksichtigung betrachten 4 A current source. In diesem Fall können wir die 20-V-Spannungsquelle beseitigen, indem wir sie kurzschließen. Das modifizierte Schaltbild ist in der folgenden Abbildung dargestellt.

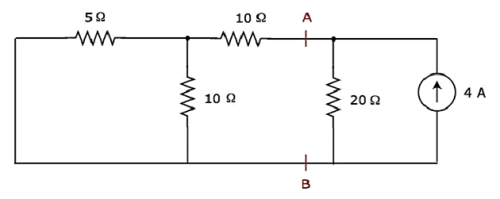
In der obigen Schaltung befinden sich drei Widerstände links von den Klemmen A und B. Wir können diese Widerstände durch einen einzigen ersetzen equivalent resistor. Hier sind 5 Ω- und 10 Ω-Widerstände parallel geschaltet und die gesamte Kombination ist mit dem 10 Ω-Widerstand in Reihe geschaltet.

Das equivalent resistance links von den Terminals A & B.

$$ R_ {AB} = \ lgroup \ frac {5 \ times 10} {5 + 10} \ rgroup + 10 = \ frac {10} {3} + 10 = \ frac {40} {3} \ Omega $$

Das vereinfachte Schaltbild ist in der folgenden Abbildung dargestellt.

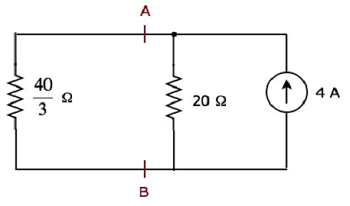
Wir können den Strom finden, der durch den 20 Ω-Widerstand fließt, indem wir verwenden current division principle.

$$ I_2 = I_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$

Ersetzen Sie $ I_S = 4A, \: R_1 = \ frac {40} {3} \ Omega $ und $ R_2 = 20 \ Omega $ in der obigen Gleichung.

$$ I_2 = 4 \ lgroup \ frac {\ frac {40} {3}} {\ frac {40} {3} + 20} \ rgroup = 4 \ lgroup \ frac {40} {100} \ rgroup = 1,6 A. $$

Daher ist der durch den 20 Ω Widerstand fließende Strom 1.6 A, wenn nur 4 A Stromquelle berücksichtigt wird.

Step 3 - Wir werden den Strom durch den 20 Ω Widerstand des gegebenen Stromkreises fließen lassen, indem wir das tun addition of two currents dass wir in Schritt 1 und Schritt 2 bekommen haben. Mathematisch kann es geschrieben werden als

$$ I = I_1 + I_2 $$

Ersetzen Sie die Werte von I ₁ und I ₂ in der obigen Gleichung.

$$ I = 0,4 + 1,6 = 2 A $$

Daher ist der Strom, der durch den 20 Ω-Widerstand einer gegebenen Schaltung fließt, 2 A.

Note - Wir können den Überlagerungssatz nicht direkt anwenden, um die Menge von zu finden powerWird an jeden Widerstand geliefert, der in einer linearen Schaltung vorhanden ist, indem einfach die an diesen Widerstand aufgrund jeder unabhängigen Quelle gelieferten Leistungen addiert werden. Vielmehr können wir entweder den durch diesen Widerstand fließenden Gesamtstrom oder die Spannung über diesen Widerstand unter Verwendung des Überlagerungssatzes berechnen und daraus die an diesen Widerstand gelieferte Leistungsmenge unter Verwendung von $ I ^ 2 R $ oder $ \ frac {V ^ 2} berechnen {R} $.