Satz der maximalen Leistungsübertragung
Die von einer Last empfangene Energiemenge ist ein wichtiger Parameter in elektrischen und elektronischen Anwendungen. In Gleichstromkreisen können wir die Last mit einem Widerstand mit einem Widerstand von R L Ohm darstellen. In ähnlicher Weise können wir es in Wechselstromkreisen mit einer komplexen Last mit einer Impedanz von Z L Ohm darstellen.
Maximum power transfer theorem gibt an, dass die Gleichspannungsquelle nur dann maximale Leistung an den Widerstand mit variabler Last liefert, wenn der Lastwiderstand gleich dem Quellenwiderstand ist.
Ähnlich, Maximum power transfer theorem gibt an, dass die Wechselspannungsquelle der variablen komplexen Last nur dann maximale Leistung liefert, wenn die Lastimpedanz gleich dem komplexen Konjugat der Quellenimpedanz ist.
Lassen Sie uns in diesem Kapitel den Satz der maximalen Leistungsübertragung für Gleichstromkreise diskutieren.
Beweis des Satzes der maximalen Leistungsübertragung
Ersetzen Sie ein beliebiges lineares Netzwerk oder eine Schaltung mit zwei Anschlüssen auf der linken Seite des Widerstands mit variabler Last und einem Widerstand von R L Ohm durch ein Thevenin-Ersatzschaltbild. Wir wissen, dass das Ersatzschaltbild von Thevenin einer praktischen Spannungsquelle ähnelt.
Dieses Konzept ist in den folgenden Abbildungen dargestellt.
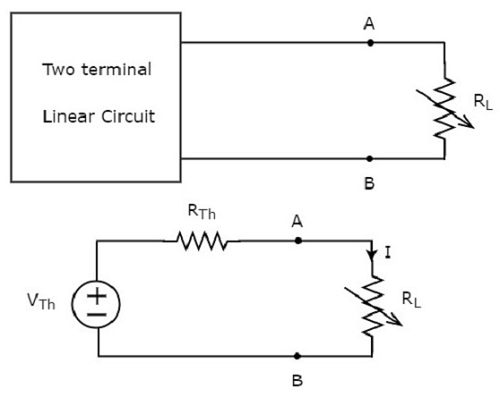
Die über den Lastwiderstand abgegebene Leistung beträgt
$$ P_L = I ^ 2 R_L $$
Ersetzen Sie $ I = \ frac {V_ {Th}} {R_ {Th} + R_L} $ in der obigen Gleichung.
$$ P_L = \ lgroup \ frac {V_ {Th}} {(R_ {Th} + R_L)} \ rgroup ^ 2 R_L $$
$ \ Rightarrow P_L = {V_ {Th}} ^ 2 \ lbrace \ frac {R_L} {(R_ {Th} + R_L) ^ 2} \ rbrace $ Equation 1
Bedingung für maximale Kraftübertragung
Für Maximum oder Minimum ist die erste Ableitung Null. Differenzieren Sie also Gleichung 1 in Bezug auf R L und machen Sie sie gleich Null.
$$ \ frac {dP_L} {dR_L} = {V_ {Th}} ^ 2 \ lbrace \ frac {(R_ {Th} + R_L) ^ 2 \ mal 1 - R_L \ mal 2 (R_ {Th} + R_L) } {(R_ {Th} + R_L) ^ 4} \ rbrace = 0 $$
$$ \ Rightarrow (R_ {Th} + R_L) ^ 2 -2R_L (R_ {Th} + R_L) = 0 $$
$$ \ Rightarrow (R_ {Th} + R_L) (R_ {Th} + R_L - 2R_L) = 0 $$
$$ \ Rightarrow (R_ {Th} - R_L) = 0 $$
$$ \ Rightarrow R_ {Th} = R_L \: oder \: R_L = R_ {Th} $$
deshalb, die condition for maximum powerDie Verlustleistung über die Last beträgt $ R_L = R_ {Th} $. Das heißt, wenn der Wert des Lastwiderstands gleich dem Wert des Quellenwiderstands ist, dh dem Widerstand von Thevenin, ist die über die Last abgegebene Leistung von maximalem Wert.
Der Wert der maximalen Leistungsübertragung
Ersetzen Sie $ R_L = R_ {Th} \: \ & \: P_L = P_ {L, Max} $ in Gleichung 1.
$$ P_ {L, Max} = {V_ {Th}} ^ 2 \ lbrace \ frac {R_ {Th}} {(R_ {Th} + R_ {Th}) ^ 2} \ rbrace $$
$$ P_ {L, Max} = {V_ {Th}} ^ 2 \ lbrace \ frac {R_ {Th}} {4 {R_ {Th}} ^ 2} \ rbrace $$
$$ \ Rightarrow P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {Th}} $$
$$ \ Rightarrow P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {L}}, \: da \: R_ {L} = R_ {Th} $$
deshalb, die maximum amount of power auf die Last übertragen wird
$$ P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4R_ {L}} = \ frac {{V_ {Th}} ^ 2} {4R_ {Th}} $$
Effizienz der maximalen Kraftübertragung
Wir können die Effizienz der maximalen Leistungsübertragung $ \ eta_ {Max} $ anhand der folgenden Formel berechnen.
$ \ eta_ {Max} = \ frac {P_ {L, Max}} {P_S} $ Equation 2
Wo,
$ P_ {L, Max} $ ist die maximale Leistung, die auf die Last übertragen wird.
$ P_S $ ist die von der Quelle erzeugte Energiemenge.
Das amount of power generated von der Quelle ist
$$ P_S = I ^ 2 R_ {Th} + I ^ 2 R_L $$
$$ \ Rightarrow P_S = 2 I ^ 2 R_ {Th}, \: da \: R_ {L} = R_ {Th} $$
Ersetzen Sie $ I = \ frac {V_ {Th}} {2 R_ {Th}} $ in der obigen Gleichung.
$$ P_S = 2 \ lgroup \ frac {V_ {Th}} {2 R_ {Th}} \ rgroup ^ 2 R_ {Th} $$
$$ \ Rightarrow P_S = 2 \ lgroup \ frac {{V_ {Th}} ^ 2} {4 {R_ {Th}} ^ 2} \ rgroup R_ {Th} $$
$$ \ Rightarrow P_S = \ frac {{V_ {Th}} ^ 2} {2 R_ {Th}} $$
Ersetzen Sie die Werte von $ P_ {L, Max} $ und $ P_S $ in Gleichung 2.
$$ \ eta_ {Max} = \ frac {\ lgroup \ frac {{V_ {Th}} ^ 2} {4R_ {Th}} \ rgroup} {\ lgroup \ frac {{V_ {Th}} ^ 2} { 2R_ {Th}} \ rgroup} $$
$$ \ Rightarrow \ eta_ {Max} = \ frac {1} {2} $$
Wir können die Effizienz der maximalen Leistungsübertragung in Bezug auf darstellen percentage wie folgt -
$$ \% \ eta_ {Max} = \ eta_ {Max} \ times 100 \% $$
$$ \ Rightarrow \% \ eta_ {Max} = \ lgroup \ frac {1} {2} \ rgroup \ times 100 \% $$
$$ \ Rightarrow \% \ eta_ {Max} = 50 \% $$
Daher ist der Wirkungsgrad der maximalen Leistungsübertragung 50 %.
Beispiel
Finden Sie die maximum powerDies kann an den Lastwiderstand R L der in der folgenden Abbildung gezeigten Schaltung geliefert werden .
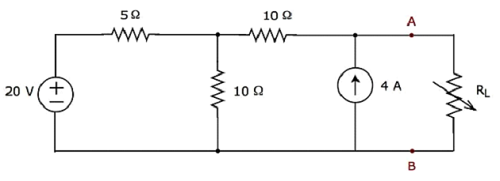
Step 1- In Thevenins Theorem-Kapitel haben wir das Thevenin-Ersatzschaltbild auf der linken Seite der Klemmen A und B berechnet. Wir können dieses Schaltkreis jetzt verwenden. Dies ist in der folgenden Abbildung dargestellt.
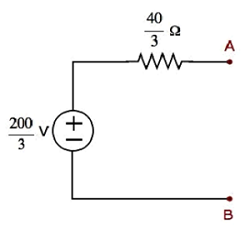
Hier ist Thevenins Spannung $ V_ {Th} = \ frac {200} {3} V $ und Thevenins Widerstand $ R_ {Th} = \ frac {40} {3} \ Omega $
Step 2- Ersetzen Sie den Teil des Stromkreises, der sich links von den Klemmen A und B des angegebenen Stromkreises befindet, durch das oben genannte Thevenin-Ersatzschaltbild. Das resultierende Schaltbild ist in der folgenden Abbildung dargestellt.

Step 3- Wir können die maximale Leistung ermitteln, die an den Lastwiderstand R L abgegeben wird, indem wir die folgende Formel verwenden.
$$ P_ {L, Max} = \ frac {{V_ {Th}} ^ 2} {4 R_ {Th}} $$
Ersetzen Sie $ V_ {Th} = \ frac {200} {3} V $ und $ R_ {Th} = \ frac {40} {3} \ Omega $ in der obigen Formel.
$$ P_ {L, Max} = \ frac {\ lgroup \ frac {200} {3} \ rgroup ^ 2} {4 \ lgroup \ frac {40} {3} \ rgroup} $$
$$ P_ {L, Max} = \ frac {250} {3} W $$
deshalb, die maximum power das an den Lastwiderstand RL der gegebenen Schaltung geliefert wird, ist $ \ mathbf {\ frac {250} {3}} $ W