Netzwerktheorie - Umwandlung von Delta in Stern
Im vorherigen Kapitel haben wir ein Beispiel für einen problembezogenen äquivalenten Widerstand erörtert. Dort haben wir die berechnetequivalent resistancezwischen den Klemmen A & B des gegebenen Stromnetzes leicht. Denn in jedem Schritt haben wir die Kombination von Widerständen erhalten, die entweder in Reihenform oder in Parallelform verbunden sind.
In einigen Situationen ist es jedoch schwierig, das Netzwerk zu vereinfachen, indem der vorherige Ansatz befolgt wird. Zum Beispiel sind die Widerstände entweder in Delta (δ) -Form oder Sternform verbunden. In solchen Situationen müssen wirconvertdas Netzwerk von einer Form zur anderen, um es durch Verwendung einer Reihenkombination oder einer Parallelkombination weiter zu vereinfachen. Lassen Sie uns in diesem Kapitel über dieDelta to Star Conversion.
Delta Network
Folgendes berücksichtigen delta network wie in der folgenden Abbildung gezeigt.
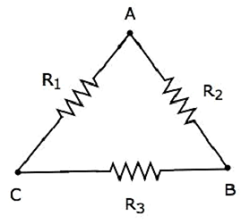
Die folgenden Gleichungen repräsentieren die equivalent resistance zwischen zwei Terminals des Delta-Netzwerks, wenn das dritte Terminal offen gehalten wird.
$$ R_ {AB} = \ frac {(R_1 + R_3) R_2} {R_1 + R_2 + R_3} $$
$$ R_ {BC} = \ frac {(R_1 + R_2) R_3} {R_1 + R_2 + R_3} $$
$$ R_ {CA} = \ frac {(R_2 + R_3) R_1} {R_1 + R_2 + R_3} $$
Star Network
Die folgende Abbildung zeigt die equivalent star network entsprechend dem obigen Delta-Netzwerk.
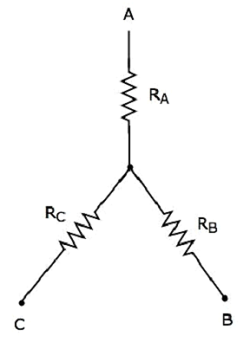
Die folgenden Gleichungen repräsentieren die equivalent resistance zwischen zwei Terminals des Sternnetzwerks, wenn das dritte Terminal offen gehalten wird.
$$ R_ {AB} = R_A + R_B $$
$$ R_ {BC} = R_B + R_C $$
$$ R_ {CA} = R_C + R_A $$
Star Network Resistances in Bezug auf Delta Network Resistances
Wir erhalten die folgenden Gleichungen, indem wir die Terme auf der rechten Seite der obigen Gleichungen gleichsetzen, für die die Terme auf der linken Seite gleich sind.
$ R_A + R_B = \ frac {(R_1 + R_3) R_2} {R_1 + R_2 + R_3} $ Equation 1
$ R_B + R_C = \ frac {(R_1 + R_2) R_3} {R_1 + R_2 + R_3} $ Equation 2
$ R_C + R_A = \ frac {(R_2 + R_3) R_1} {R_1 + R_2 + R_3} $ Equation 3
Durch Hinzufügen der obigen drei Gleichungen erhalten wir
$$ 2 (R_A + R_B + R_C) = \ frac {2 (R_1 R_2 + R_2 R_3 + R_3 R_1)} {R_1 + R_2 + R_3} $$
$ \ Rightarrow R_A + R_B + R_C = \ frac {R_1 R_2 + R_2 R_3 + R_3 R_1} {R_1 + R_2 + R_3} $ Equation 4
Subtrahieren Sie Gleichung 2 von Gleichung 4.
$ R_A + R_B + R_C - (R_B + R_C) = \ frac {R_1 R_2 + R_2 R_3 + R_3 R_1} {R_1 + R_2 + R_3} - \ frac {(R_1 + R_2) R_3} {R_1 + R_2 + R_3} $
$$ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $$
Durch Subtrahieren von Gleichung 3 von Gleichung 4 erhalten wir
$$ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $$
Durch Subtrahieren von Gleichung 1 von Gleichung 4 erhalten wir
$$ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $$
Unter Verwendung der obigen Beziehungen können wir die Widerstände des Sternnetzwerks aus den Widerständen des Delta-Netzwerks ermitteln. Auf diese Weise können wir a konvertierendelta network in ein star network.
Beispiel
Berechnen wir die resistances of star network, die dem Delta-Netzwerk entsprechen, wie in der folgenden Abbildung gezeigt.
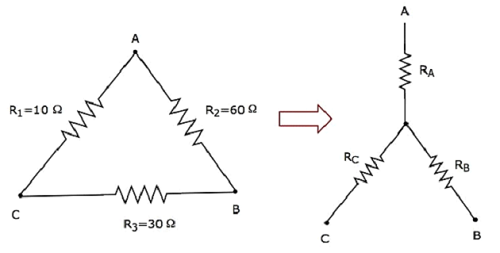
Angenommen resistances of delta networkals R 1 = 10 Ω, R 2 = 60 Ω und R 3 = 30 Ω.
Wir kennen die folgenden Beziehungen der Widerstände des Sternnetzwerks in Bezug auf die Widerstände des Delta-Netzwerks.
$$ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $$
$$ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $$
$$ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $$
Ersetzen Sie die Werte von R 1 , R 2 und R 3 durch die obigen Gleichungen.
$$ R_A = \ frac {10 \ times 60} {10 + 60 + 30} = \ frac {600} {100} = 6 \ Omega $$
$$ R_B = \ frac {60 \ mal 30} {10 + 60 + 30} = \ frac {1800} {100} = 18 \ Omega $$
$$ R_C = \ frac {30 \ times 10} {10 + 60 + 30} = \ frac {300} {100} = 3 \ Omega $$
Also haben wir die Widerstände des Sternennetzwerks als RA = 6 Ω, RB = 18 Ω und RC = 3 Ω, die den Widerständen des gegebenen Delta-Netzwerks entsprechen.