Netzwerktheorie - Stern-Delta-Umwandlung
Im vorherigen Kapitel haben wir die Umwandlung des Delta-Netzwerks in ein äquivalentes Sternnetzwerk erörtert. Lassen Sie uns nun über die Umwandlung des Sternnetzwerks in ein äquivalentes Delta-Netzwerk diskutieren. Diese Konvertierung wird als bezeichnetStar to Delta Conversion.
Im vorigen Kapitel haben wir die resistances of star network vom Delta-Netzwerk als
$ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $ Equation 1
$ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $ Equation 2
$ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $ Equation 3
Delta Network Resistances in Bezug auf Star Network Resistances
Manipulieren wir die obigen Gleichungen, um die Widerstände des Delta-Netzwerks in Form der Widerstände des Sternnetzwerks zu erhalten.
Multiply jeder Satz von zwei Gleichungen und dann add.
$$ R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 ^ 2 R_3 + R_2 R_3 ^ 2 R_1 + R_3 R_1 ^ 2 R_2} {(R_1 + R_2 + R_3) ^ 2} $$
$$ \ Rightarrow R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 R_3 (R_1 + R_2 + R_3)} {(R_1 + R_2 + R_3) ^ 2} $$
$ \ Rightarrow R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 R_3} {R_1 + R_2 + R_3} $ Equation 4
Durch Teilen von Gleichung 4 mit Gleichung 2 erhalten wir
$$ \ frac {R_A R_B + R_B R_C + R_C R_A} {R_B} = R_1 $$
$$ \ Rightarrow R_1 = R_C + R_A + \ frac {R_C R_A} {R_B} $$
Durch Teilen von Gleichung 4 mit Gleichung 3 erhalten wir
$$ R_2 = R_A + R_B + \ frac {R_A R_B} {R_C} $$
Durch Teilen von Gleichung 4 mit Gleichung 1 erhalten wir
$$ R_3 = R_B + R_C + \ frac {R_B R_C} {R_A} $$
Unter Verwendung der obigen Beziehungen können wir die Widerstände des Delta-Netzwerks aus den Widerständen des Sternnetzwerks ermitteln. Auf diese Weise können wir konvertierenstar network into delta network.
Beispiel
Berechnen wir die resistances of delta network, die dem des Sternennetzwerks entsprechen, wie in der folgenden Abbildung gezeigt.
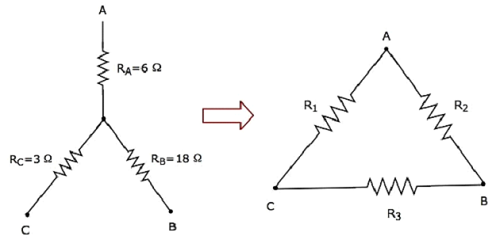
Angenommen resistances of star networkals R A = 6 Ω, R B = 18 Ω und R C = 3 Ω .
Wir kennen die folgenden Beziehungen der resistances of delta network in Bezug auf die Widerstände des Sternennetzwerks.
$$ R_1 = R_C + R_A + \ frac {R_C R_A} {R_B} $$
$$ R_2 = R_A + R_B + \ frac {R_A R_B} {R_C} $$
$$ R_3 = R_B + R_C + \ frac {R_B R_C} {R_A} $$
Ersetzen Sie die Werte von R A , R B und R C durch die obigen Gleichungen.
$$ R_1 = 3 + 6 + \ frac {3 \ times 6} {18} = 9 + 1 = 10 \ Omega $$
$$ R_2 = 6 + 18 + \ frac {6 \ times 18} {3} = 24 + 36 = 60 \ Omega $$
$$ R_3 = 18 + 3 + \ frac {18 \ times 3} {6} = 21 + 9 = 30 \ Omega $$
Also haben wir die Widerstände des Delta-Netzwerks als R1 = 10 Ω, R2 = 60 Ω und R3 = 30 Ω, die den Widerständen des gegebenen Sternnetzwerks entsprechen.