Netzwerktheorie - Reaktion von Wechselstromkreisen
Im vorherigen Kapitel haben wir das Einschwingverhalten und das stationäre Verhalten des Gleichstromkreises erörtert. Lassen Sie uns in diesem Kapitel das diskutierenresponse of AC circuit. Die Konzepte des Einschwingverhaltens und des stationären Ansprechverhaltens, die wir im vorherigen Kapitel erörtert haben, werden auch hier nützlich sein.
Ermitteln der Reaktion der Serie RL-Schaltung
Folgendes berücksichtigen series RL circuit Diagramm.

In der obigen Schaltung ist die switch wurde behalten openbis zu t = 0 und es wurde bei t = 0 geschlossen . Daher ist die Wechselspannungsquelle mit einer Spitzenspannung von V m Volt bis zu diesem Zeitpunkt nicht mit der Serien-RL-Schaltung verbunden. Daher gibt esno initial current fließt durch den Induktor.
Der Schaltplan, wenn die switch ist in closed Position, ist in der folgenden Abbildung dargestellt.
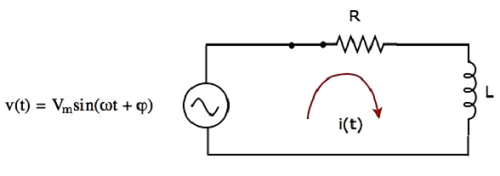
Nun fließt der Strom i (t) in der gesamten Schaltung, da die Wechselspannungsquelle mit einer Spitzenspannung von V m Volt an die Serien-RL-Schaltung angeschlossen ist.
Wir wissen, dass der Strom i (t) , der durch die obige Schaltung fließt, zwei Terme hat, einen, der den Übergangsteil darstellt, und einen anderen Term, der den stationären Zustand darstellt.
Mathematisch kann es dargestellt werden als
$ i (t) = i_ {Tr} (t) + i_ {ss} (t) $Equation 1
Wo,
$ i_ {Tr} (t) $ ist das Einschwingverhalten des durch die Schaltung fließenden Stroms.
$ i_ {ss} (t) $ ist die stationäre Antwort des durch die Schaltung fließenden Stroms.
Im vorherigen Kapitel haben wir das Einschwingverhalten des durch die Serien-RL-Schaltung fließenden Stroms erhalten. Es hat die Form von $ Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} $.
Ersetzen Sie $ i_ {Tr} (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} $ in Gleichung 1.
$ i (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + i_ {ss} (t) $Equation 2
Berechnung des stationären Stroms
Wenn ein sinusförmiges Signal als Eingang für einen linearen Stromkreis angelegt wird, erzeugt es einen stationären Ausgang, der auch a ist sinusoidal signal. Sowohl das sinusförmige Eingangs- als auch das Ausgangssignal haben die gleiche Frequenz, jedoch unterschiedliche Amplituden und Phasenwinkel.
Wir können die stationäre Reaktion eines Stromkreises berechnen, wenn er von einer sinusförmigen Spannungsquelle mit angeregt wird Laplace Transform approach.
Das S-Domänen-Schaltbild, wenn die switch ist in closed Position, ist in der folgenden Abbildung dargestellt.
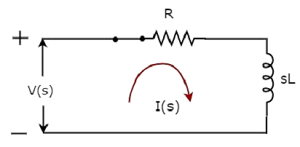
In der obigen Schaltung sind alle Größen und Parameter in dargestellt s-domain. Dies sind die Laplace-Transformationen von Zeitbereichsgrößen und -parametern.
Das Transfer function der obigen Schaltung ist
$$ H (s) = \ frac {I (s)} {V (s)} $$
$$ \ Rightarrow H (s) = \ frac {1} {Z (s)} $$
$$ \ Rightarrow H (s) = \ frac {1} {R + sL} $$
Ersetzen Sie $ s = j \ omega $ in der obigen Gleichung.
$$ H (j \ omega) = \ frac {1} {R + j \ omega L} $$
Magnitude of $ \ mathbf {\ mathit {H (j \ omega)}} $ ist
$$ | H (j \ omega) | = \ frac {1} {\ sqrt {R ^ 2 + {\ omega} ^ 2} L ^ 2} $$
Phase angle of $ \ mathbf {\ mathit {H (j \ omega)}} $ ist
$$ \ angle H (j \ omega) = -tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup $$
Wir werden das bekommen steady state current $ i_ {ss} (t) $, indem Sie die folgenden zwei Schritte ausführen:
Multiplizieren Sie die Spitzenspannung der sinusförmigen Eingangsspannung und die Größe von $ H (j \ omega) $.
Addieren Sie die Phasenwinkel der sinusförmigen Eingangsspannung und $ H (j \ omega) $.
Das steady state current $ i_ {ss} (t) $ wird sein
$$ i_ {ss} (t) = \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$
Ersetzen Sie den Wert von $ i_ {ss} (t) $ in Gleichung 2.
$ i (t) = Ke ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $Equation 3
Wir wissen, dass in der Schaltung kein Anfangsstrom vorhanden ist. Ersetzen Sie daher in Gleichung 3 t = 0 & i (t) = 0 , um den Wert der Konstanten K zu ermitteln.
$$ 0 = Ke ^ {- \ lgroup \ frac {0} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ Omega (0) + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$
$$ \ Rightarrow 0 = K + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi - tan ^ {- 1} \ lgroup \ frac {\ Omega L} {R} \ rgroup \ rgroup $$
$$ \ Rightarrow K = - \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$
Ersetzen Sie den Wert von K in Gleichung 3.
$ i (t) = - \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup e ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} + \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2 }} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $Equation 4
Gleichung 4 stellt den Strom dar, der durch die Serien-RL-Schaltung fließt, wenn er von einer sinusförmigen Spannungsquelle angeregt wird. Es hat zwei Begriffe. Der erste und der zweite Term repräsentieren das Einschwingverhalten bzw. das stationäre Ansprechverhalten des Stroms.
Wir können neglect the first termvon Gleichung 4, weil sein Wert sehr viel kleiner als eins sein wird. Der resultierende Strom, der durch die Schaltung fließt, ist also
$$ i (t) = \ frac {V_m} {\ sqrt {R ^ 2 + {\ omega} ^ 2 L ^ 2}} sin \ lgroup \ omega t + \ varphi - tan ^ {- 1} \ lgroup \ frac {\ omega L} {R} \ rgroup \ rgroup $$
Es enthält nur die steady state term. Daher können wir nur das stationäre Verhalten von Wechselstromkreisen finden und das Einschwingverhalten vernachlässigen.