Netzwerktheorie - Passive Elemente
In diesem Kapitel werden die passiven Elemente wie Widerstand, Induktor und Kondensator ausführlich erläutert. Beginnen wir mit Widerständen.
Widerstand
Die Hauptfunktionalität des Widerstands besteht darin, dem Stromfluss entweder entgegenzuwirken oder ihn einzuschränken. Daher werden die Widerstände verwendet, um den Stromfluss und / oder die Teilungsspannung zu begrenzen.
Der durch den Widerstand fließende Strom sei I Ampere und die Spannung über ihm beträgt V Volt. Dassymbol des Widerstands zusammen mit Strom I und Spannung V sind in der folgenden Abbildung dargestellt.
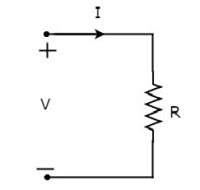
Gemäß Ohm’s lawDie Spannung am Widerstand ist das Produkt des durch ihn fließenden Stroms und des Widerstands dieses Widerstands. Mathematicallykann es dargestellt werden als
$ V = IR $ Equation 1
$ \ Rightarrow I = \ frac {V} {R} $Equation 2
Wo, R ist der Widerstand eines Widerstands.
Aus Gleichung 2 können wir schließen, dass der durch den Widerstand fließende Strom direkt proportional zur angelegten Spannung am Widerstand und umgekehrt proportional zum Widerstand des Widerstands ist.
Power in einem elektrischen Schaltungselement kann dargestellt werden als
$ P = VI $Equation 3
Ersetzen Sie Gleichung 1 in Gleichung 3.
$ P = (IR) I $
$ \ Rightarrow P = I ^ 2 R $ Equation 4
Ersetzen Sie Gleichung 2 in Gleichung 3.
$ P = V \ lgroup \ frac {V} {R} \ rgroup $
$ \ Rightarrow P = \ frac {V ^ 2} {R} $ Equation 5
Wir können also die im Widerstand verbrauchte Leistung unter Verwendung einer der in den Gleichungen 3 bis 5 genannten Formeln berechnen.
Induktor
Im Allgemeinen haben Induktoren eine Anzahl von Windungen. Daher erzeugen sie einen magnetischen Fluss, wenn Strom durch sie fließt. Die Menge des gesamten magnetischen Flusses, der von einem Induktor erzeugt wird, hängt also vom Strom ab, den I durch ihn fließt, und sie haben eine lineare Beziehung.
Mathematicallykann geschrieben werden als
$$ \ Psi \: \ alpha \: I $$
$$ \ Rightarrow \ Psi = LI $$
Wo,
Ψ ist der gesamte magnetische Fluss
L ist die Induktivität eines Induktors
Der durch den Induktor fließende Strom sei I Ampere und die Spannung über ihm beträgt V Volt. Dassymbolder Induktivität zusammen mit Strom I und Spannung V sind in der folgenden Abbildung dargestellt.
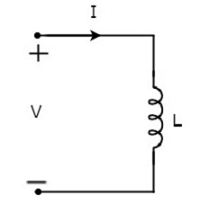
Gemäß Faraday’s lawkann die Spannung über der Induktivität wie folgt geschrieben werden
$$ V = \ frac {d \ Psi} {dt} $$
Ersetzen Sie Ψ = LI in der obigen Gleichung.
$$ V = \ frac {d (LI)} {dt} $$
$$ \ Rightarrow V = L \ frac {dI} {dt} $$
$$ \ Rightarrow I = \ frac {1} {L} \ int V dt $$
Aus den obigen Gleichungen können wir schließen, dass es eine gibt linear relationship zwischen der Spannung über der Induktivität und dem durch sie fließenden Strom.
Wir wissen das power in einem elektrischen Schaltungselement kann dargestellt werden als
$$ P = VI $$
Ersetzen Sie $ V = L \ frac {dI} {dt} $ in der obigen Gleichung.
$$ P = \ lgroup L \ frac {dI} {dt} \ rgroup I $$
$$ \ Rightarrow P = LI \ frac {dI} {dt} $$
Durch Integration der obigen Gleichung erhalten wir die energy in einem Induktor gespeichert als
$$ W = \ frac {1} {2} LI ^ 2 $$
Der Induktor speichert also die Energie in Form eines Magnetfeldes.
Kondensator
Im Allgemeinen hat ein Kondensator zwei leitende Platten, die durch ein dielektrisches Medium getrennt sind. Wenn eine positive Spannung an den Kondensator angelegt wird, speichert er positive Ladung. In ähnlicher Weise speichert eine negative Ladung, wenn eine negative Spannung an den Kondensator angelegt wird.
Die im Kondensator gespeicherte Ladungsmenge hängt also von der angelegten Spannung ab Vdarüber und sie haben eine lineare Beziehung. Mathematisch kann es geschrieben werden als
$$ Q \: \ alpha \: V $$
$$ \ Rightarrow Q = CV $$
Wo,
Q ist die im Kondensator gespeicherte Ladung.
C ist die Kapazität eines Kondensators.
Der durch den Kondensator fließende Strom sei I Ampere und die Spannung über ihm beträgt V Volt. Das Symbol des Kondensators zusammen mit Strom I und Spannung V ist in der folgenden Abbildung dargestellt.
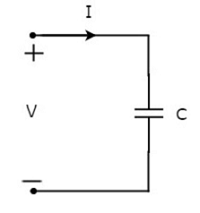
Wir wissen, dass die current ist nichts als das time rate of flow of charge. Mathematisch kann es dargestellt werden als
$$ I = \ frac {dQ} {dt} $$
Ersetzen Sie $ Q = CV $ in der obigen Gleichung.
$$ I = \ frac {d (CV)} {dt} $$
$$ \ Rightarrow I = C \ frac {dV} {dt} $$
$$ \ Rightarrow V = \ frac {1} {C} \ int I dt $$
Aus den obigen Gleichungen können wir schließen, dass es eine gibt linear relationship zwischen der Spannung am Kondensator und dem durch ihn fließenden Strom.
Wir wissen das power in einem elektrischen Schaltungselement kann dargestellt werden als
$$ P = VI $$
Ersetzen Sie $ I = C \ frac {dV} {dt} $ in der obigen Gleichung.
$$ P = V \ lgroup C \ frac {dV} {dt} \ rgroup $$
$$ \ Rightarrow P = CV \ frac {dV} {dt} $$
Durch Integration der obigen Gleichung erhalten wir die energy im Kondensator gespeichert als
$$ W = \ frac {1} {2} CV ^ 2 $$
Der Kondensator speichert also die Energie in Form eines elektrischen Feldes.