Netzwerktheorie - Netzanalyse
Bei der Netzanalyse werden die Ströme berücksichtigt, die durch jedes Netz fließen. Daher wird die Netzanalyse auch als bezeichnetMesh-current method.
EIN branchist ein Pfad, der zwei Knoten verbindet und ein Schaltungselement enthält. Wenn ein Zweig nur zu einem Netz gehört, entspricht der Verzweigungsstrom dem Netzstrom.
Wenn ein Zweig zwei Maschen gemeinsam ist, ist der Zweigstrom gleich der Summe (oder Differenz) zweier Maschenströme, wenn sie in derselben (oder entgegengesetzter) Richtung liegen.
Verfahren der Netzanalyse
Befolgen Sie diese Schritte, während Sie ein elektrisches Netzwerk oder einen Stromkreis mithilfe der Netzanalyse lösen.
Step 1 - Identifizieren Sie die meshes und beschriften Sie die Maschenströme entweder im oder gegen den Uhrzeigersinn.
Step 2 - Beobachten Sie die Strommenge, die durch jedes Element fließt, in Form von Maschenströmen.
Step 3 - Schreiben mesh equationszu allen Maschen. Die Maschengleichung wird erhalten, indem zuerst KVL und dann das Ohmsche Gesetz angewendet werden.
Step 4 - Lösen Sie die in Schritt 3 erhaltenen Netzgleichungen, um die zu erhalten mesh currents.
Jetzt können wir den Strom, der durch jedes Element fließt, und die Spannung über jedem Element, das in dem gegebenen Netzwerk vorhanden ist, unter Verwendung von Maschenströmen finden.
Beispiel
Ermitteln Sie die Spannung am 30 Ω-Widerstand mit Mesh analysis.
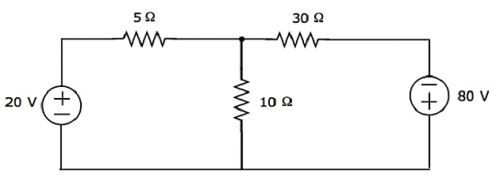
Step 1- In der obigen Schaltung befinden sich zwei Maschen. Dasmesh currentsI 1 und I 2 werden im Uhrzeigersinn betrachtet. Diese Maschenströme sind in der folgenden Abbildung dargestellt.
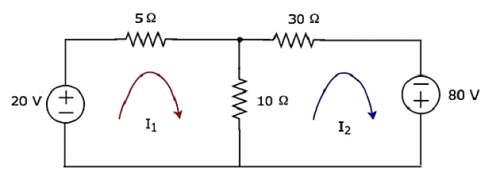
Step 2- Der Maschenstrom I 1 fließt durch eine 20-V-Spannungsquelle und einen 5-Ω-Widerstand. In ähnlicher Weise fließt der Maschenstrom I 2 durch einen 30 Ω-Widerstand und eine Spannungsquelle von -80 V. Die Differenz zweier Maschenströme I 1 und I 2 fließt jedoch durch einen 10 Ω-Widerstand, da dies der gemeinsame Zweig zweier Maschen ist.
Step 3 - In diesem Fall werden wir bekommen two mesh equationsda es zwei Maschen in der gegebenen Schaltung gibt. Wenn wir die Netzgleichungen schreiben, nehmen wir an, dass der Netzstrom dieses bestimmten Netzes größer ist als alle anderen Netzströme der Schaltung.
Das mesh equation des ersten Netzes ist
$$ 20 - 5I_1 -10 (I_1 - I_2) = 0 $$
$$ \ Rightarrow 20 - 15I_1 + 10I_2 = 0 $$
$$ \ Rightarrow 10I_2 = 15I_1 - 20 $$
Teilen Sie die obige Gleichung mit 5.
$$ 2I_2 = 3I_1 - 4 $$
Multiplizieren Sie die obige Gleichung mit 2.
$ 4I_2 = 6I_1 - 8 $ Equation 1
Das mesh equation des zweiten Netzes ist
$$ - 10 (I_2 - I_1) - 30I_2 + 80 = 0 $$
Teilen Sie die obige Gleichung mit 10.
$$ - (I_2 - I_1) - 3I_2 + 8 = 0 $$
$$ \ Rightarrow -4I_2 + I_1 + 8 = 0 $$
$ 4I_2 = I_1 + 8 $ Equation 2
Step 4- Finden der Maschenströme I 1 und I 2 durch Lösen von Gleichung 1 und Gleichung 2.
Die Terme auf der linken Seite von Gleichung 1 und Gleichung 2 sind gleich. Setzen Sie daher die Terme auf der rechten Seite von Gleichung 1 und Gleichung 2 gleich, um den Wert von I 1 zu finden .
$$ 6I_1 - 8 = I_1 + 8 $$
$$ \ Rightarrow 5I_1 = 16 $$
$$ \ Rightarrow I_1 = \ frac {16} {5} A $$
Ersetzen Sie den I 1 -Wert in Gleichung 2.
$$ 4I_2 = \ frac {16} {5} + 8 $$
$$ \ Rightarrow 4I_2 = \ frac {56} {5} $$
$$ \ Rightarrow I_2 = \ frac {14} {5} A $$
Wir haben also die Maschenströme I 1 und I 2 als $ \ mathbf {\ frac {16} {5}} $ erhaltenA und $ \ mathbf {\ frac {14} {5}} $ A beziehungsweise.
Step 5- Der durch den 30 Ω-Widerstand fließende Strom ist nichts anderes als der Maschenstrom I 2 und entspricht $ \ frac {14} {5} $ A. Nun können wir die Spannung am 30 Ω-Widerstand unter Verwendung des Ohmschen Gesetzes ermitteln.
$$ V_ {30 \ Omega} = I_2 R $$
Ersetzen Sie die Werte von I 2 und R in der obigen Gleichung.
$$ V_ {30 \ Omega} = \ lgroup \ frac {14} {5} \ rgroup 30 $$
$$ \ Rightarrow V_ {30 \ Omega} = 84V $$
Daher beträgt die Spannung am 30 Ω-Widerstand der gegebenen Schaltung 84 V.
Note 1- Aus dem obigen Beispiel können wir schließen, dass wir m-Maschengleichungen lösen müssen, wenn der Stromkreis m-Maschen hat. Aus diesem Grund können wir die Netzanalyse wählen, wenn die Anzahl der Netze geringer ist als die Anzahl der Hauptknoten (mit Ausnahme des Referenzknotens) eines Stromkreises.
Note 2 - Wir können entweder Knotenanalyse oder Netzanalyse wählen, wenn die Anzahl der Netze gleich der Anzahl der Hauptknoten (mit Ausnahme des Referenzknotens) in einem Stromkreis ist.