Teoria sieci - konwersja delta do gwiazdy
W poprzednim rozdziale omówiliśmy przykładową rezystancję równoważną związaną z problemem. Tam obliczyliśmyequivalent resistancełatwo między zaciskami A i B danej sieci elektrycznej. Ponieważ na każdym kroku otrzymaliśmy kombinację rezystorów połączonych szeregowo lub równolegle.
Jednak w niektórych sytuacjach trudno jest uprościć sieć, stosując poprzednie podejście. Na przykład rezystory połączone w kształcie trójkąta (δ) lub gwiazdy. W takich sytuacjach musimyconvertsieć jednej postaci do drugiej w celu dalszego uproszczenia jej poprzez zastosowanie kombinacji szeregowej lub kombinacji równoległej. W tym rozdziale omówimy tematDelta to Star Conversion.
Delta Network
Rozważ następujące delta network jak pokazano na poniższym rysunku.
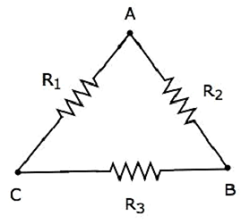
Poniższe równania reprezentują equivalent resistance między dwoma terminalami sieci delta, gdy trzeci terminal jest otwarty.
$$ R_ {AB} = \ frac {(R_1 + R_3) R_2} {R_1 + R_2 + R_3} $$
$$ R_ {BC} = \ frac {(R_1 + R_2) R_3} {R_1 + R_2 + R_3} $$
$$ R_ {CA} = \ frac {(R_2 + R_3) R_1} {R_1 + R_2 + R_3} $$
Star Network
Poniższy rysunek przedstawia equivalent star network odpowiadające powyższej sieci delta.
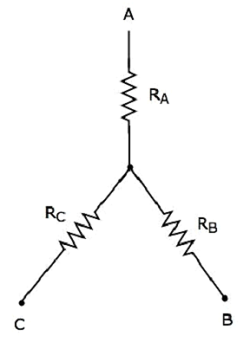
Poniższe równania reprezentują equivalent resistance między dwoma terminalami sieci gwiazdy, gdy trzeci terminal jest otwarty.
$$ R_ {AB} = R_A + R_B $$
$$ R_ {BC} = R_B + R_C $$
$$ R_ {CA} = R_C + R_A $$
Star Network Resistances w kategoriach Delta Network Resistances
Otrzymamy następujące równania, zrównując wyrazy po prawej stronie powyższych równań, dla których wyrazy po lewej stronie są takie same.
$ R_A + R_B = \ frac {(R_1 + R_3) R_2} {R_1 + R_2 + R_3} $ Equation 1
$ R_B + R_C = \ frac {(R_1 + R_2) R_3} {R_1 + R_2 + R_3} $ Equation 2
$ R_C + R_A = \ frac {(R_2 + R_3) R_1} {R_1 + R_2 + R_3} $ Equation 3
Dodając powyższe trzy równania, otrzymamy
$$ 2 (R_A + R_B + R_C) = \ frac {2 (R_1 R_2 + R_2 R_3 + R_3 R_1)} {R_1 + R_2 + R_3} $$
$ \ Rightarrow R_A + R_B + R_C = \ frac {R_1 R_2 + R_2 R_3 + R_3 R_1} {R_1 + R_2 + R_3} $ Equation 4
Odejmij równanie 2 od równania 4.
$ R_A + R_B + R_C - (R_B + R_C) = \ frac {R_1 R_2 + R_2 R_3 + R_3 R_1} {R_1 + R_2 + R_3} - \ frac {(R_1 + R_2) R_3} {R_1 + R_2 + R_3} $
$$ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $$
Odejmując równanie 3 od równania 4, otrzymamy
$$ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $$
Odejmując równanie 1 od równania 4, otrzymamy
$$ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $$
Korzystając z powyższych zależności, możemy znaleźć opory sieci gwiazdowej na podstawie rezystancji sieci delta. W ten sposób możemy przekonwertować plikdelta network do star network.
Przykład
Obliczmy resistances of star network, które są równoważne sieci typu trójkąt, jak pokazano na poniższym rysunku.
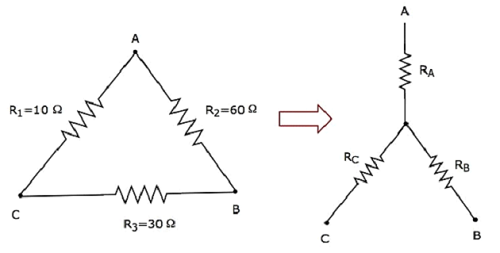
Biorąc pod uwagę resistances of delta networkjako R 1 = 10 Ω, R 2 = 60 Ω i R 3 = 30 Ω.
Znamy następujące relacje oporów sieci gwiazdowej w kategoriach rezystancji sieci delta.
$$ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $$
$$ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $$
$$ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $$
Zastąp wartości R 1 , R 2 i R 3 w powyższych równaniach.
$$ R_A = \ frac {10 \ times 60} {10 + 60 + 30} = \ frac {600} {100} = 6 \ Omega $$
$$ R_B = \ frac {60 \ times 30} {10 + 60 + 30} = \ frac {1800} {100} = 18 \ Omega $$
$$ R_C = \ frac {30 \ times 10} {10 + 60 + 30} = \ frac {300} {100} = 3 \ Omega $$
Więc otrzymaliśmy rezystancje sieci gwiazd jako RA = 6 Ω, RB = 18 Ω i RC = 3 Ω, które są równoważne rezystancjom danej sieci trójkątnej.