Teoria sieci - twierdzenie o superpozycji
Superposition theoremopiera się na koncepcji liniowości między odpowiedzią a wzbudzeniem obwodu elektrycznego. Stwierdza, że odpowiedź w określonej gałęzi obwodu liniowego, gdy wiele niezależnych źródeł działa w tym samym czasie, jest równoważna sumie odpowiedzi spowodowanych przez każde niezależne źródło działające w tym samym czasie.
W tej metodzie rozważymy tylko one independent sourcena czas. Musimy więc wyeliminować pozostałe niezależne źródła z obwodu. Możemy wyeliminować źródła napięcia, zwierając ich dwa zaciski i analogicznie, źródła prądu, otwierając oba zaciski.
Dlatego musimy znaleźć odpowiedź w konkretnej branży ‘n’ timesjeśli istnieje „n” niezależnych źródeł. Odpowiedzią w konkretnej gałęzi może być prąd przepływający przez tę gałąź lub napięcie w tej gałęzi.
Procedura twierdzenia o superpozycji
Wykonaj poniższe kroki, aby znaleźć odpowiedź w określonej gałęzi za pomocą twierdzenia o superpozycji.
Step 1 - Znajdź odpowiedź w określonej branży, biorąc pod uwagę jedno niezależne źródło i eliminując pozostałe niezależne źródła obecne w sieci.
Step 2 - Powtórz krok 1 dla wszystkich niezależnych źródeł obecnych w sieci.
Step 3 - Dodaj wszystkie odpowiedzi, aby uzyskać ogólną odpowiedź w określonej gałęzi, gdy wszystkie niezależne źródła są obecne w sieci.
Przykład
Znajdź prąd przepływający przez rezystor 20 Ω następującego obwodu za pomocą superposition theorem.
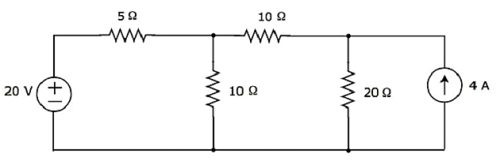
Step 1 - Znajdźmy prąd przepływający przez rezystor 20 Ω, biorąc pod uwagę tylko 20 V voltage source. W takim przypadku możemy wyeliminować źródło prądu 4 A, otwierając jego obwód. Zmodyfikowany schemat obwodu pokazano na poniższym rysunku.

W powyższym obwodzie jest tylko jeden główny węzeł oprócz uziemienia. Więc możemy użyćnodal analysismetoda. Napięcie węzłowe V 1 jest oznaczone na poniższym rysunku. Tutaj V 1 jest napięciem z węzła 1 względem masy.
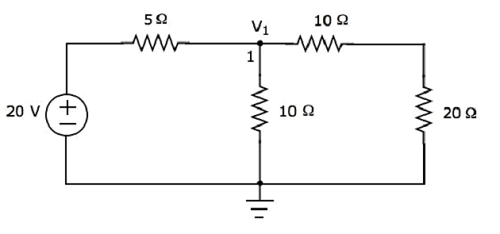
Plik nodal equation w węźle 1 jest
$$ \ frac {V_1 - 20} {5} + \ frac {V_1} {10} + \ frac {V_1} {10 + 20} = 0 $$
$$ \ Rightarrow \ frac {6V_1 - 120 + 3V_1 + V_1} {30} = 0 $$
$$ \ Rightarrow 10V_1 = 120 $$
$$ \ Rightarrow V_1 = 12V $$
Plik current flowing through 20 Ω resistor można znaleźć, wykonując następujące uproszczenie.
$$ I_1 = \ frac {V_1} {10 + 20} $$
Zastąp wartość V 1 w powyższym równaniu.
$$ I_1 = \ frac {12} {10 + 20} = \ frac {12} {30} = 0,4 A $$
Dlatego prąd przepływający przez rezystor 20 Ω jest 0.4 A, gdy rozważane jest tylko źródło napięcia 20 V.
Step 2 - Znajdźmy prąd przepływający przez rezystor 20 Ω, biorąc pod uwagę tylko 4 A current source. W takim przypadku możemy wyeliminować źródło napięcia 20 V, wykonując jego zwarcie. Zmodyfikowany schemat obwodu pokazano na poniższym rysunku.
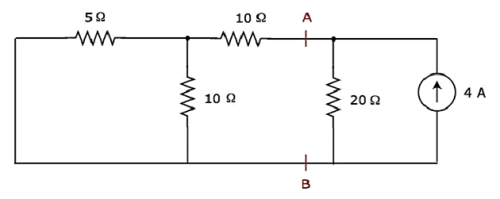
W powyższym obwodzie po lewej stronie zacisków A i B znajdują się trzy rezystory. Możemy zastąpić te rezystory pojedynczym equivalent resistor. Tutaj rezystory 5 Ω i 10 Ω są połączone równolegle, a cała kombinacja jest połączona szeregowo z rezystorem 10 Ω.
Plik equivalent resistance na lewo od terminali A i B będą
$$ R_ {AB} = \ lgroup \ frac {5 \ times 10} {5 + 10} \ rgroup + 10 = \ frac {10} {3} + 10 = \ frac {40} {3} \ Omega $$
Poniższy rysunek przedstawia uproszczony schemat połączeń.
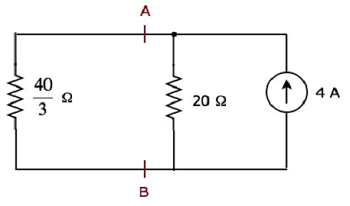
Prąd przepływający przez rezystor 20 Ω możemy znaleźć używając current division principle.
$$ I_2 = I_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
Podstaw $ I_S = 4A, \: R_1 = \ frac {40} {3} \ Omega $ i $ R_2 = 20 \ Omega $ w powyższym równaniu.
$$ I_2 = 4 \ lgroup \ frac {\ frac {40} {3}} {\ frac {40} {3} + 20} \ rgroup = 4 \ lgroup \ frac {40} {100} \ rgroup = 1,6 A $$
Dlatego prąd przepływający przez rezystor 20 Ω jest 1.6 A, gdy brane jest pod uwagę źródło prądu tylko 4 A.
Step 3 - Prąd płynący przez rezystor 20 Ω danego obwodu uzyskamy wykonując addition of two currents który otrzymaliśmy w kroku 1 i kroku 2. Matematycznie można to zapisać jako
$$ I = I_1 + I_2 $$
Podstawimy wartości I 1 i I 2 w powyższym równaniu.
$$ I = 0,4 + 1,6 = 2 A $$
Zatem prąd przepływający przez rezystor 20 Ω danego obwodu wynosi 2 A.
Note - Nie możemy bezpośrednio zastosować twierdzenia o superpozycji w celu obliczenia ilości powerdostarczane do dowolnego rezystora, który jest obecny w obwodzie liniowym, po prostu przez dodanie mocy dostarczanych do tego rezystora z powodu każdego niezależnego źródła. Możemy raczej obliczyć albo całkowity prąd przepływający przez ten rezystor, albo napięcie na tym rezystorze, używając twierdzenia o superpozycji, a na tej podstawie możemy obliczyć ilość mocy dostarczonej do tego rezystora za pomocą $ I ^ 2 R $ lub $ \ frac {V ^ 2} {R} $.