Teoria sieci - elementy pasywne
W tym rozdziale omówimy szczegółowo elementy pasywne, takie jak rezystor, cewka indukcyjna i kondensator. Zacznijmy od rezystorów.
Rezystor
Główną funkcją rezystora jest przeciwdziałanie lub ograniczanie przepływu prądu elektrycznego. W związku z tym rezystory są używane w celu ograniczenia wielkości przepływu prądu i / lub dzielenia (współdzielenia) napięcia.
Niech prąd przepływający przez rezystor ma wartość 1 amperów, a napięcie na nim wynosi V woltów. Pliksymbol rezystora wraz z prądem, I i napięciem, V pokazano na poniższym rysunku.
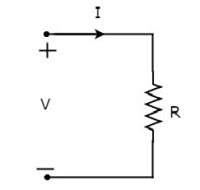
Według Ohm’s law, napięcie na rezystorze jest iloczynem przepływającego przez niego prądu i rezystancji tego rezystora. Mathematically, można go przedstawić jako
$ V = IR $ Equation 1
$ \ Rightarrow I = \ frac {V} {R} $Equation 2
Gdzie, R jest rezystancją rezystora.
Z równania 2 możemy wywnioskować, że prąd przepływający przez rezystor jest wprost proporcjonalny do przyłożonego napięcia na rezystorze i odwrotnie proporcjonalny do rezystancji rezystora.
Power w elemencie obwodu elektrycznego można przedstawić jako
$ P = VI $Equation 3
Zastąp równanie 1 w równaniu 3.
$ P = (IR) I $
$ \ Rightarrow P = I ^ 2 R $ Equation 4
Zastąp równanie 2 w równaniu 3.
$ P = V \ lgroup \ frac {V} {R} \ rgroup $
$ \ Rightarrow P = \ frac {V ^ 2} {R} $ Equation 5
Możemy więc obliczyć ilość mocy rozproszonej w rezystorze za pomocą jednego ze wzorów wymienionych w równaniach od 3 do 5.
Induktor
Ogólnie cewki będą miały liczbę zwojów. W związku z tym wytwarzają strumień magnetyczny, gdy przepływa przez nie prąd. Tak więc wielkość całkowitego strumienia magnetycznego wytwarzanego przez cewkę indukcyjną zależy od prądu, przez który przepływam i mają one liniową zależność.
Mathematically, można go zapisać jako
$$ \ Psi \: \ alpha \: I $$
$$ \ Rightarrow \ Psi = LI $$
Gdzie,
Ψ to całkowity strumień magnetyczny
L jest indukcyjnością cewki indukcyjnej
Niech prąd przepływający przez cewkę wynosi 1 amper, a napięcie na nim wynosi V woltów. Pliksymbolcewki indukcyjnej wraz z prądem I i napięciem V pokazano na poniższym rysunku.
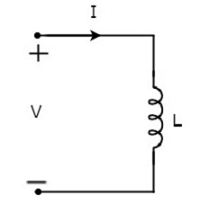
Według Faraday’s law, napięcie na cewce można zapisać jako
$$ V = \ frac {d \ Psi} {dt} $$
Zastąpić * F = LI w powyższym równaniu.
$$ V = \ frac {d (LI)} {dt} $$
$$ \ Rightarrow V = L \ frac {dI} {dt} $$
$$ \ Rightarrow I = \ frac {1} {L} \ int V dt $$
Z powyższych równań możemy wywnioskować, że istnieje linear relationship między napięciem na cewce a przepływającym przez nią prądem.
Wiemy to power w elemencie obwodu elektrycznego można przedstawić jako
$$ P = VI $$
Podstaw $ V = L \ frac {dI} {dt} $ w powyższym równaniu.
$$ P = \ lgroup L \ frac {dI} {dt} \ rgroup I $$
$$ \ Rightarrow P = LI \ frac {dI} {dt} $$
Całkując powyższe równanie, otrzymamy energy przechowywane w induktorze jako
$$ W = \ frac {1} {2} LI ^ 2 $$
Zatem induktor przechowuje energię w postaci pola magnetycznego.
Kondensator
Ogólnie kondensator ma dwie przewodzące płytki, oddzielone dielektrykiem. Jeśli do kondensatora zostanie przyłożone napięcie dodatnie, to zachowuje ładunek dodatni. Podobnie, jeśli napięcie ujemne zostanie przyłożone do kondensatora, wówczas przechowuje ładunek ujemny.
Tak więc ilość ładunku przechowywanego w kondensatorze zależy od przyłożonego napięcia Vw poprzek i mają liniową zależność. Matematycznie można to zapisać jako
$$ Q \: \ alpha \: V $$
$$ \ Rightarrow Q = CV $$
Gdzie,
Q to ładunek przechowywany w kondensatorze.
C to pojemność kondensatora.
Niech prąd przepływający przez kondensator ma wartość 1 amperów, a napięcie na nim wynosi V woltów. Symbol kondensatora wraz z prądem I i napięciem V pokazano na poniższym rysunku.
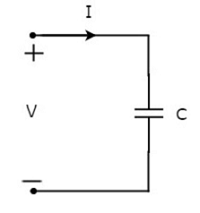
Wiemy, że current to nic innego jak time rate of flow of charge. Matematycznie można to przedstawić jako
$$ I = \ frac {dQ} {dt} $$
Zastąp $ Q = CV $ w powyższym równaniu.
$$ I = \ frac {d (CV)} {dt} $$
$$ \ Rightarrow I = C \ frac {dV} {dt} $$
$$ \ Rightarrow V = \ frac {1} {C} \ int I dt $$
Z powyższych równań możemy wywnioskować, że istnieje linear relationship między napięciem na kondensatorze a przepływającym przez niego prądem.
Wiemy to power w elemencie obwodu elektrycznego można przedstawić jako
$$ P = VI $$
Podstaw $ I = C \ frac {dV} {dt} $ w powyższym równaniu.
$$ P = V \ lgroup C \ frac {dV} {dt} \ rgroup $$
$$ \ Rightarrow P = CV \ frac {dV} {dt} $$
Całkując powyższe równanie, otrzymamy energy przechowywane w kondensatorze jako
$$ W = \ frac {1} {2} CV ^ 2 $$
Zatem kondensator magazynuje energię w postaci pola elektrycznego.