Teoria sieci - odpowiedź obwodów prądu stałego

Jeśli sygnał wyjściowy obwodu elektrycznego dla wejścia zmienia się w czasie, nazywa się go jako time response. Odpowiedź czasowa składa się z następujących dwóch części.

• Reakcja przejściowa
• Odpowiedź w stanie stacjonarnym

W tym rozdziale omówimy najpierw te dwie odpowiedzi, a następnie obserwujemy te dwie odpowiedzi w obwodzie szeregowym RL, gdy jest on wzbudzany przez źródło napięcia stałego.

Reakcja przejściowa

Po przyłożeniu sygnału wejściowego do obwodu elektrycznego wyjście osiąga stan ustalony po pewnym czasie. Tak więc wyjście będzie w stanie przejściowym, dopóki nie przejdzie do stanu ustalonego. Dlatego odpowiedź obwodu elektrycznego w stanie przejściowym jest znana jakotransient response.

Reakcja przejściowa będzie wynosić zero dla dużych wartości „t”. Idealnie, ta wartość „t” powinna wynosić nieskończoność. Ale praktyczniefive time constants są wystarczające.

Obecność lub brak przemijających

Stany przejściowe występują w odpowiedzi z powodu sudden changew źródłach, które są doprowadzane do obwodu elektrycznego i / lub w wyniku przełączania. Istnieją dwie możliwe czynności przełączania. To jest przełącznik otwierania i zamykania.

• Plik transient część będzie not presentw odpowiedzi obwodu elektrycznego lub sieci, jeśli zawiera tylko rezystancje. Dlategoresistor ma możliwość regulacji dowolnej wartości napięcia i prądu.

• Plik transient part occurs w odpowiedzi obwodu elektrycznego lub sieci z powodu obecności elementów magazynujących energię, takich jak inductor and capacitor. Ponieważ nie mogą natychmiast zmienić energii zgromadzonej w tych elementach.

Zachowanie cewki indukcyjnej

Załóżmy, że działanie przełączające ma miejsce w chwili t = 0.Inductor currentnie zmienia się natychmiast po przełączeniu. Oznacza to, że wartość prądu cewki indukcyjnej tuż po przełączeniu będzie taka sama, jak tuż przed przełączeniem.

Matematycznie można to przedstawić jako

$$ i_L (0 ^ +) = i_L (0 ^ -) $$

Zachowanie kondensatorów

Plik capacitor voltagenie zmienia się natychmiastowo, podobnie jak prąd cewki indukcyjnej, gdy następuje przełączenie. Oznacza to, że wartość napięcia kondensatora tuż po przełączeniu będzie taka sama, jak tuż przed przełączeniem.

Matematycznie można to przedstawić jako

$$ v_c (0 ^ +) = v_c (0 ^ -) $$

Odpowiedź w stanie stacjonarnym

Część odpowiedzi czasowej, która pozostaje nawet po tym, jak odpowiedź przejściowa stała się wartością zerową dla dużych wartości „t”, jest znana jako steady state response. Oznacza to, że w stanie ustalonym nie będzie żadnej przejściowej części odpowiedzi.

Zachowanie cewki indukcyjnej

Jeżeli niezależne źródło jest podłączone do obwodu elektrycznego lub sieci mającej jeden lub więcej cewek indukcyjnych i rezystorów (opcjonalnie) przez długi czas, wówczas ten obwód elektryczny lub sieć jest w stanie ustalonym. Dlatego energia zmagazynowana w cewce (cewkach) tego obwodu elektrycznego jest maksymalna i stała.

Matematycznie można to przedstawić jako

$ W_L = \ frac {L {i_L} ^ 2} {2} = $ Maksymalna i stała

$ \ Rightarrow i_L = $ Maksymalna i stała

Dlatego cewka działa jak constant current source w stanie ustalonym.

Napięcie na cewce będzie wynosić

$$ V_L = L \ frac {di_ {L}} {dt} = 0V $$

Tak więc cewka działa jak short circuit w stanie ustalonym.

Zachowanie kondensatorów

Jeżeli niezależne źródło jest podłączone do obwodu elektrycznego lub sieci mającej jeden lub więcej kondensatorów i rezystorów (opcjonalnie) przez długi czas, wówczas ten obwód elektryczny lub sieć jest w stanie ustalonym. Dlatego energia zmagazynowana w kondensatorze (-ach) tego obwodu elektrycznego jest maksymalna i stała.

Matematycznie można to przedstawić jako

$ W_c = \ frac {C {v_c} ^ 2} {2} = $ Maksymalna i stała

$ \ Rightarrow v_c = $ Maksymalna i stała

Dlatego kondensator działa jak constant voltage source w stanie ustalonym.

Prąd przepływający przez kondensator będzie

$$ i_c = C \ frac {dv_c} {dt} = 0A $$

Tak więc kondensator działa jako open circuit w stanie ustalonym.

Znajdowanie odpowiedzi obwodu szeregowego RL

Rozważ następujące series RL circuit diagram.

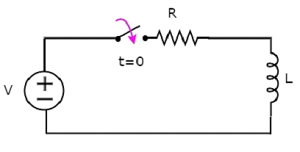
W powyższym obwodzie switch był przechowywany openaż do t = 0 i zostało zamknięte w t = 0. Tak więc źródło napięcia stałego o woltach V nie jest dołączane do obwodu szeregowego RL do tej chwili. Dlatego jestno initial current przepływa przez cewkę.

Schemat obwodu, gdy switch jest w closed położenie pokazano na poniższym rysunku.

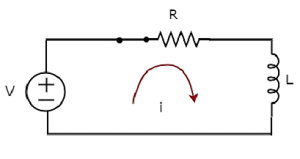
Teraz prąd i płynie w całym obwodzie, ponieważ źródło napięcia stałego ma V woltów jest podłączony do obwodu szeregowego RL.

Teraz aplikuj KVL wokół pętli.

$$ V = Ri + L \ frac {di} {dt} $$

$ \ frac {di} {dt} + \ lgroup \ frac {R} {L} \ rgroup i = \ frac {V} {L} $Equation 1

Powyższe równanie jest równaniem różniczkowym pierwszego rzędu i ma postać

$ \ frac {dy} {dt} + Py = Q $Equation 2

Przez comparing Równanie 1 i równanie 2, otrzymamy następujące zależności.

$$ x = t $$

$$ y = i $$

$$ P = \ frac {R} {L} $$

$$ Q = \ frac {V} {L} $$

Plik solution z równania 2 będzie

$ ye ^ {\ int p dx} = \ int Q e ^ {\ int p dx} dx + k $Equation 3

Gdzie, k jest stała.

Zastąp wartości x, y, P i Q w równaniu 3.

$ ie ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} = \ int (\ frac {V} {L}) \ lgroup e ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} \ rgroup dt + k $

$ \ Rightarrow ie ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ int e ^ {\ lgroup \ frac {R} {L} \ rgroup t} dt + k $

$ \ Rightarrow ie ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ lbrace \ frac {e ^ {\ lgroup \ frac {R} {L} \ rgroup} t} {\ frac {R} {L}} \ rbrace + k $

$ \ Rightarrow i = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup} t $Equation 4

Wiemy, że w obwodzie nie ma prądu początkowego. Stąd podstawienie, t = 0 i = 0 w równaniu 4, aby znaleźć wartość stałej k.

$$ 0 = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup (0)} $$

$$ 0 = \ frac {V} {R} + k (1) $$

$$ k = - \ frac {V} {R} $$

Zastąp wartość k w równaniu 4.

$$ i = \ frac {V} {R} + \ lgroup - \ frac {V} {R} \ rgroup e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $$

$$ i = \ frac {V} {R} - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $$

Dlatego też current przepływający przez obwód jest

$ i = - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} + \ frac {V} {R} $Equation 5

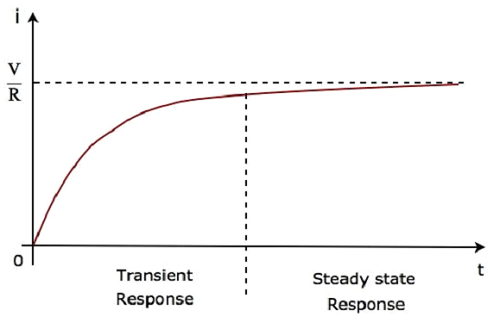
Tak więc reakcja obwodu szeregowego RL, gdy jest wzbudzana przez źródło napięcia stałego, ma następujące dwa wyrazy.

• Pierwszy wyraz $ - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $ odpowiada transient response.

• Drugi termin $ \ frac {V} {R} $ odpowiada steady state response. Te dwie odpowiedzi przedstawiono na poniższym rysunku.

Możemy przepisać równanie 5 w następujący sposób -

$ i = \ frac {V} {R} \ lgroup 1 - e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} \ rgroup $

$ \ Rightarrow i = \ frac {V} {R} \ lgroup 1 - e ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} \ rgroup $Equation 6

Gdzie, τ jest time constant a jego wartość jest równa $ \ frac {L} {R} $.

Równanie 5 i 6 są takie same. Ale możemy łatwo zrozumieć powyższy przebieg prądu przepływającego przez obwód z równania 6, zastępując kilka wartościt jak 0, τ, 2τ, 5τ itd.

W powyższym przebiegu prądu przepływającego przez obwód, odpowiedź przejściowa będzie prezentować do pięciu stałych czasowych od zera, podczas gdy odpowiedź w stanie ustalonym będzie występować od pięciu stałych czasowych wzwyż.