Przykładowy problem obwodów równoważnych
W poprzednim rozdziale omówiliśmy indywidualnie obwody równoważne w kombinacji szeregowej i kombinacji równoległej. W tym rozdziale rozwiążmy przykładowy problem, rozważając zarówno szeregowe, jak i równoległe kombinacje podobnych elementów pasywnych.
Przykład
Znajdźmy plik equivalent resistance przez zaciski A i B następującej sieci elektrycznej.

Uzyskamy równoważną rezystancję na zaciskach A i B, minimalizując powyższą sieć do pojedynczego rezystora między tymi dwoma zaciskami. W tym celu musimyidentify the combination of resistors które są połączone szeregowo i równolegle, a następnie znajdź równoważny opór odpowiedniej formy na każdym kroku.
Podana sieć elektryczna to modified w poniższy formularz, jak pokazano na poniższym rysunku.
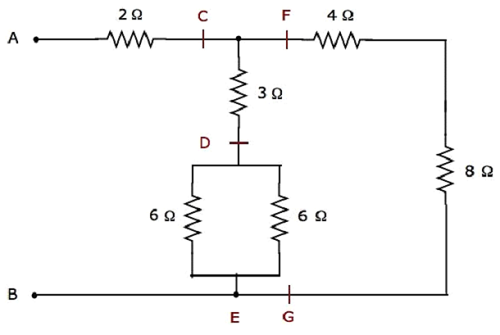
Na powyższym rysunku litery od C do G służą do oznaczania różnych zacisków.
Step 1 - W powyższej sieci dwa 6 Ω resistors są podłączone parallel. Tak więc równoważna rezystancja między D i E będzie wynosić 3 Ω. Można to uzyskać, wykonując następujące uproszczenie.
$$ R_ {DE} = \ frac {6 \ times 6} {6 + 6} = \ frac {36} {12} = 3 \ Omega $$
W powyższej sieci rezystory 4 Ω i 8 Ω są podłączone series. Tak więc równoważna rezystancja między F i G będzie wynosić 12 Ω. Można to uzyskać, wykonując następujące uproszczenie.
$$ R_ {FG} = 4 + 8 = 12 \ Omega $$
Step 2 - Uproszczona instalacja elektryczna network after Step 1 pokazano na poniższym rysunku.
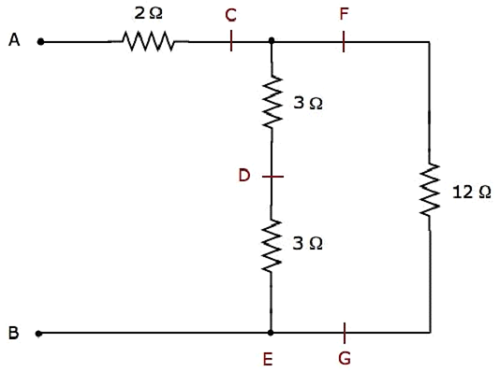
W powyższej sieci dwa 3 Ω resistors są podłączone series. Tak więc równoważny opór między C i E będzie6 Ω. Można to uzyskać, wykonując następujące uproszczenie.
$$ R_ {CE} = 3 + 3 = 6 \ Omega $$
Step 3 - Uproszczona instalacja elektryczna network after Step 2 pokazano na poniższym rysunku.

W powyższej sieci rezystory 6 Ω i 12 Ω są podłączone parallel. Tak więc równoważna rezystancja między C i B będzie wynosić 4 Ω. Można to uzyskać, wykonując następujące uproszczenie.
$$ R_ {CB} = \ frac {6 \ times 12} {6 + 12} = \ frac {72} {18} = 4 \ Omega $$
Step 4 - Uproszczona instalacja elektryczna network after Step 3 pokazano na poniższym rysunku.
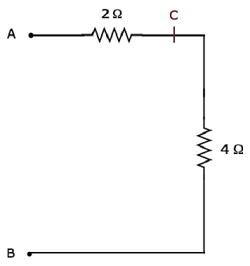
W powyższej sieci rezystory 2 Ω i 4 Ω są podłączone seriesmiędzy zaciskami A i B. Zatem równoważna rezystancja między A i B będzie wynosić 6 Ω. Można to uzyskać, wykonując następujące uproszczenie.
$$ R_ {AB} = 2 + 4 = 6 \ Omega $$
Dlatego równoważna rezystancja między zaciskami A i B danej sieci elektrycznej wynosi 6 Ω.