Teoria sieci - rezonans szeregowy
Resonancewystępuje w obwodach elektrycznych z powodu obecności elementów magazynujących energię, takich jak cewka i kondensator. Jest to podstawowa koncepcja, na podstawie której odbiorniki radiowe i telewizyjne są projektowane w taki sposób, aby mogły wybierać tylko żądaną częstotliwość stacji.
Tam są two typesrezonansów, a mianowicie rezonansu szeregowego i rezonansu równoległego. Są one klasyfikowane na podstawie elementów sieci połączonych szeregowo lub równolegle. W tym rozdziale omówimy rezonans szeregowy.
Schemat obwodu rezonansu szeregowego
Jeśli rezonans występuje w obwodzie szeregowym RLC, nazywa się go as Series Resonance. Rozważ następująceseries RLC circuit, który jest reprezentowany w dziedzinie wskazowej.
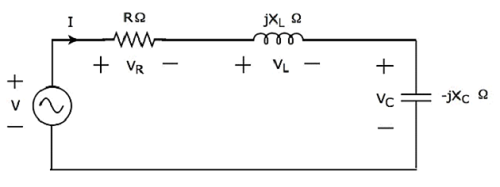
Tutaj elementy bierne, takie jak rezystor, cewka i kondensator, są połączone szeregowo. Ta cała kombinacja jest dostępnaseries z wejściowym źródłem napięcia sinusoidalnego.
Zastosować KVL wokół pętli.
$$ V - V_R - V_L - V_C = 0 $$
$$ \ Rightarrow V - IR - I (j X_L) - I (-j X_C) = 0 $$
$$ \ Rightarrow V = IR + I (j X_L) + I (-j X_C) $$
$ \ Rightarrow V = I [R + j (X_L - X_C)] $Equation 1
Powyższe równanie ma postać V = IZ.
Dlatego też impedance Z obwodu szeregowego RLC
$$ Z = R + j (X_L - X_C) $$
Parametry i wielkości elektryczne w rezonansie
Teraz wyprowadźmy kolejno wartości parametrów i wielkości elektrycznych w rezonansie szeregowego obwodu RLC.
Częstotliwość rezonansowa
Częstotliwość, przy której występuje rezonans, nazywana jest as resonant frequency fr. W szeregu RLC rezonans obwodu występuje, gdy wyimaginowany człon impedancji Z wynosi zero, tj. Wartość $ X_L - X_C $ powinna być równa zero.
$$ \ Rightarrow X_L = X_C $$
Podstaw $ X_L = 2 \ pi f L $ i $ X_C = \ frac {1} {2 \ pi f C} $ w powyższym równaniu.
$$ 2 \ pi f L = \ frac {1} {2 \ pi f C} $$
$$ \ Rightarrow f ^ 2 = \ frac {1} {(2 \ pi) ^ 2 LC} $$
$$ \ Rightarrow f = \ frac {1} {(2 \ pi) \ sqrt {LC}} $$
Dlatego też resonant frequency fr obwodu szeregowego RLC jest
$$ f_r = \ frac {1} {(2 \ pi) \ sqrt {LC}} $$
Gdzie, L jest indukcyjnością cewki indukcyjnej i C to pojemność kondensatora.
Plik resonant frequency fr obwodu szeregowego RLC zależy tylko od indukcyjności L i pojemność C. Ale jest niezależny od oporuR.
Impedancja
Mamy impedance Z obwodu szeregowego RLC jako
$$ Z = R + j (X_L - X_C) $$
Zastąp $ X_L = X_C $ w powyższym równaniu.
$$ Z = R + j (X_C - X_C) $$
$$ \ Rightarrow Z = R + j (0) $$
$$ \ Rightarrow Z = R $$
W rezonansie impedance Z obwodu szeregowego RLC jest równa wartości rezystancji Rtj. Z = R.
Prąd przepływający przez obwód
Podstaw $ X_L - X_C = 0 $ w równaniu 1.
$$ V = I [R + j (0)] $$
$$ \ Rightarrow V = IR $$
$$ \ Rightarrow I = \ frac {V} {R} $$
W związku z tym, current przepływający przez obwód szeregowego RLC w rezonansie to $ \ mathbf {\ mathit {I = \ frac {V} {R}}} $.
W rezonansie impedancja szeregowego obwodu RLC osiąga wartość minimalną. Stądmaximum current przepływa przez ten obwód w rezonansie.
Napięcie na rezystorze
Napięcie na rezystorze wynosi
$$ V_R = IR $$
Zastąp wartość I w powyższym równaniu.
$$ V_R = \ lgroup \ frac {V} {R} \ rgroup R $$
$$ \ Rightarrow V_R = V $$
Dlatego też voltage across resistor w rezonansie jest VR = V.
Napięcie na cewce
Napięcie na cewce wynosi
$$ V_L = I (jX_L) $$
Zastąp wartość I w powyższym równaniu.
$$ V_L = \ lgroup \ frac {V} {R} \ rgroup (jX_L) $$
$$ \ Rightarrow V_L = j \ lgroup \ frac {X_L} {R} \ rgroup V $$
$$ \ Rightarrow V_L = j QV $$
Dlatego też voltage across inductor przy rezonansie wynosi $ V_L = j QV $.
Tak więc magnitude napięcia na cewce w rezonansie będzie
$$ | V_L | = QV $$
Gdzie Q jest Quality factor a jego wartość jest równa $ \ frac {X_L} {R} $
Napięcie na kondensatorze
Napięcie na kondensatorze wynosi
$$ V_C = I (-j X_C) $$
Zastąp wartość I w powyższym równaniu.
$$ V_C = \ lgroup \ frac {V} {R} \ rgroup (-j X_C) $$
$$ \ Rightarrow V_C = -j \ lgroup \ frac {X_C} {R} \ rgroup V $$
$$ \ Rightarrow V_C = -jQV $$
Dlatego też voltage across capacitor w rezonansie to $ \ mathbf {\ mathit {V_C = -jQV}} $.
Tak więc magnitude napięcia na kondensatorze w rezonansie wyniesie
$$ | V_C | = QV $$
Gdzie Q jest Quality factor a jego wartość jest równa $ \ frac {X_ {C}} {R} $
Note - Obwód RLC z rezonansem szeregowym nosi nazwę voltage magnificationUkład, że wielkość napięcia na cewki i kondensatora jest równa Q razy sinusoidalne napięcie wejściowe V .