Teoria sieci - analiza siatki
W analizie Mesh rozważymy prądy przepływające przez każdą siatkę. Dlatego analiza siatki jest również nazywana jakoMesh-current method.
ZA branchto ścieżka, która łączy dwa węzły i zawiera element obwodu. Jeśli gałąź należy tylko do jednej siatki, wówczas prąd gałęzi będzie równy prądowi siatki.
Jeśli gałąź jest wspólna dla dwóch siatek, wówczas prąd odgałęzienia będzie równy sumie (lub różnicy) dwóch prądów siatki, gdy są one w tym samym (lub przeciwnym) kierunku.
Procedura analizy siatki
Wykonaj poniższe czynności podczas rozwiązywania dowolnej sieci lub obwodu elektrycznego za pomocą analizy siatki.
Step 1 - Zidentyfikuj meshes i oznacz prądy siatki w kierunku zgodnym lub przeciwnym do ruchu wskazówek zegara.
Step 2 - Obserwuj ilość prądu przepływającego przez każdy element pod względem prądów siatki.
Step 3 - Napisz mesh equationsdo wszystkich oczek. Równanie siatki uzyskuje się, stosując najpierw KVL, a następnie prawo Ohma.
Step 4 - Rozwiąż równania siatki uzyskane w kroku 3, aby uzyskać mesh currents.
Teraz możemy znaleźć prąd przepływający przez dowolny element i napięcie na dowolnym elemencie obecnym w danej sieci za pomocą prądów siatkowych.
Przykład
Znajdź napięcie na rezystorze 30 Ω za pomocą Mesh analysis.
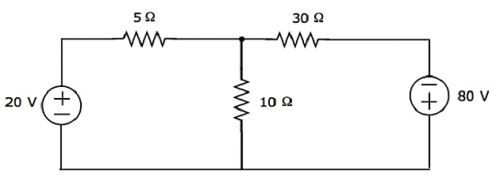
Step 1- W powyższym obwodzie są dwa oczka. Plikmesh currentsI 1 i I 2 są rozpatrywane zgodnie z ruchem wskazówek zegara. Te prądy siatkowe pokazano na poniższym rysunku.
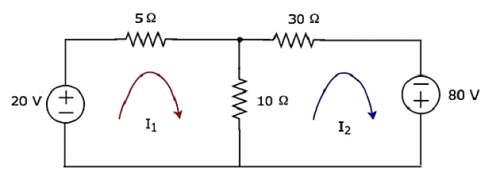
Step 2- Prąd siatki I 1 przepływa przez źródło napięcia 20 V i rezystor 5 Ω. Podobnie prąd siatki I 2 przepływa przez rezystor 30 Ω i źródło napięcia -80 V. Ale różnica dwóch prądów siatki, I 1 i I 2 , przepływa przez rezystor 10 Ω, ponieważ jest to wspólna gałąź dwóch oczek.
Step 3 - W takim razie dostaniemy two mesh equationsponieważ w danym obwodzie są dwa oczka. Kiedy piszemy równania siatki, załóżmy, że prąd siatki tej konkretnej siatki jest większy niż wszystkie inne prądy siatki w obwodzie.
Plik mesh equation pierwszej siatki jest
$$ 20 - 5I_1 -10 (I_1 - I_2) = 0 $$
$$ \ Rightarrow 20-15I_1 + 10I_2 = 0 $$
$$ \ Rightarrow 10I_2 = 15I_1 - 20 $$
Podziel powyższe równanie przez 5.
$$ 2I_2 = 3I_1 - 4 $$
Pomnóż powyższe równanie przez 2.
4I_2 $ = 6I_1 - 8 $ Equation 1
Plik mesh equation drugiej siatki jest
$$ - 10 (I_2 - I_1) - 30I_2 + 80 = 0 $$
Podziel powyższe równanie przez 10.
$$ - (I_2 - I_1) - 3I_2 + 8 = 0 $$
$$ \ Rightarrow -4I_2 + I_1 + 8 = 0 $$
4 $ I_2 = I_1 + 8 $ Equation 2
Step 4- Znajdowanie prądów siatkowych I 1 i I 2 poprzez rozwiązanie równania 1 i równania 2.
Wyrażenia po lewej stronie Równania 1 i Równania 2 są takie same. Dlatego zrównaj prawostronne wyrazy Równania 1 i Równania 2, aby znaleźć wartość I 1 .
$$ 6I_1 - 8 = I_1 + 8 $$
$$ \ Rightarrow 5I_1 = 16 $$
$$ \ Rightarrow I_1 = \ frac {16} {5} A $$
Zastąp wartość I 1 w równaniu 2.
$$ 4I_2 = \ frac {16} {5} + 8 $$
$$ \ Rightarrow 4I_2 = \ frac {56} {5} $$
$$ \ Rightarrow I_2 = \ frac {14} {5} A $$
Więc mamy prądy siatki I 1 i I 2 jako $ \ mathbf {\ frac {16} {5}} $A i $ \ mathbf {\ frac {14} {5}} $ A odpowiednio.
Step 5- Prąd przepływający przez rezystor 30 Ω to nic innego jak prąd siatki I 2 i wynosi on $ \ frac {14} {5} $ A. Teraz możemy znaleźć napięcie na rezystorze 30 Ω, korzystając z prawa Ohma.
$$ V_ {30 \ Omega} = I_2 R $$
Zastąp wartości I 2 i R w powyższym równaniu.
$$ V_ {30 \ Omega} = \ lgroup \ frac {14} {5} \ rgroup 30 $$
$$ \ Rightarrow V_ {30 \ Omega} = 84V $$
Dlatego napięcie na rezystorze 30 Ω danego obwodu wynosi 84 V.
Note 1- Z powyższego przykładu możemy wywnioskować, że musimy rozwiązać równania siatki „m”, jeśli obwód elektryczny ma oczka „m”. Dlatego możemy wybrać analizę siatki, gdy liczba oczek jest mniejsza niż liczba głównych węzłów (z wyjątkiem węzła odniesienia) dowolnego obwodu elektrycznego.
Note 2 - Możemy wybrać analizę węzłową lub analizę siatkową, gdy liczba oczek jest równa liczbie głównych węzłów (poza węzłem odniesienia) w dowolnym obwodzie elektrycznym.