Teoria sieci - obwody równoważne
Jeśli obwód składa się z dwóch lub więcej podobnych elementów pasywnych i są połączone wyłącznie szeregowo lub równolegle, to możemy je zastąpić jednym równoważnym elementem pasywnym. Stąd ten obwód nazywa sięequivalent circuit.
W tym rozdziale omówimy następujące dwa równoważne obwody.
- Obwód równoważny serii
- Równoległy obwód równoważny
Obwód równoważny serii
Jeśli zostaną podłączone podobne elementy pasywne series, wtedy ten sam prąd przepłynie przez wszystkie te elementy. Ale napięcie zostaje podzielone na każdy element.
Rozważ następujące circuit diagram.
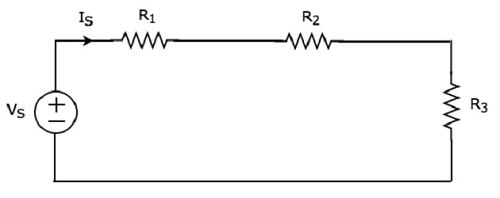
Posiada jedno źródło napięcia (V S ) i trzy rezystory o rezystancji R 1 , R 2 i R 3 . Wszystkie te elementy są połączone szeregowo. Obecny SI przepływa przez wszystkie te elementy.
Powyższy obwód ma tylko jedną siatkę. PlikKVL equation wokół tej siatki jest
$$ V_S = V_1 + V_2 + V_3 $$
Podstaw $ V_1 = I_S R_1, \: V_2 = I_S R_2 $ i $ V_3 = I_S R_3 $ w powyższym równaniu.
$$ V_S = I_S R_1 + I_S R_2 + I_S R_3 $$
$$ \ Rightarrow V_S = I_S (R_1 + R_2 + R_3) $$
Powyższe równanie ma postać $ V_S = I_S R_ {Eq} $ gdzie,
$$ R_ {Eq} = R_1 + R_2 + R_3 $$
Plik equivalent circuit diagram danego obwodu pokazano na poniższym rysunku.
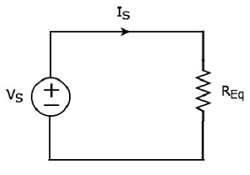
Oznacza to, że jeśli kilka rezystorów jest połączonych szeregowo, możemy je zastąpić equivalent resistor. Rezystancja tego równoważnego rezystora jest równa sumie rezystancji wszystkich tych wielu rezystorów.
Note 1- Jeśli cewki indukcyjne `` N '' o indukcyjności L 1 , L 2 , ..., L N są połączone szeregowo, toequivalent inductance będzie
$$ L_ {Eq} = L_1 + L_2 + ... + L_N $$
Note 2- Jeśli kondensatory 'N' o pojemnościach C 1 , C 2 , ..., C N są połączone szeregowo, toequivalent capacitance będzie
$$ \ frac {1} {C_ {Eq}} = \ frac {1} {C_1} + \ frac {1} {C_2} + ... + \ frac {1} {C_N} $$
Równoległy obwód równoważny
Jeśli zostaną podłączone podobne elementy pasywne parallel, to takie samo napięcie będzie utrzymywane na każdym elemencie. Ale prąd przepływający przez każdy element zostaje podzielony.
Rozważ następujące circuit diagram.

Posiada jedno źródło prądu (I S ) i trzy rezystory o rezystancji R 1 , R 2 i R 3 . Wszystkie te elementy są połączone równolegle. Napięcie (V S ) jest dostępne we wszystkich tych elementach.
Powyższy obwód ma tylko jeden główny węzeł (P) z wyjątkiem węzła uziemienia. PlikKCL equation w tym głównym węźle (P) jest
$$ I_S = I_1 + I_2 + I_3 $$
Podstaw $ I_1 = \ frac {V_S} {R_1}, \: I_2 = \ frac {V_S} {R_2} $ i $ I_3 = \ frac {V_S} {R_3} $ w powyższym równaniu.
$$ I_S = \ frac {V_S} {R_1} + \ frac {V_S} {R_2} + \ frac {V_S} {R_3} $$
$$ \ Rightarrow I_S = V_S \ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgroup $$
$$ \ Rightarrow V_S = I_S \ left [\ frac {1} {\ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgroup} \ right] $$
Powyższe równanie ma postać V S = I S R Eq gdzie,
$$ R_ {Eq} = \ frac {1} {\ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgroup} $$
$$ \ frac {1} {R_ {Eq}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} $$
Plik equivalent circuit diagram danego obwodu pokazano na poniższym rysunku.
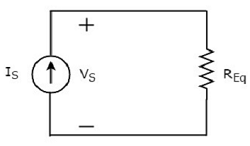
Oznacza to, że jeśli kilka rezystorów jest połączonych równolegle, możemy je zastąpić równoważnym rezystorem. Opór tegoequivalent resistor jest równe odwrotności sumy odwrotności każdego oporu wszystkich tych wielokrotnych rezystorów.
Note 1- Jeżeli dławiki `` N '' o indukcyjności L 1 , L 2 , ..., L N są połączone równolegle, toequivalent inductance będzie
$$ \ frac {1} {L_ {Eq}} = \ frac {1} {L_1} + \ frac {1} {L_2} + ... + \ frac {1} {L_N} $$
Note 2- Jeśli kondensatory `` N '' o pojemnościach C 1 , C 2 , ..., C N są połączone równolegle, toequivalent capacitance będzie
$$ C_ {Eq} = C_1 + C_2 + ... + C_N $$