Zasady podziału ilości energii elektrycznej
W tym rozdziale omówimy następujące dwie zasady podziału wielkości elektrycznych.
- Bieżąca zasada podziału
- Zasada podziału napięcia
Bieżąca zasada podziału
Kiedy dwa lub więcej elementów pasywnych jest połączonych równolegle, ilość prądu przepływającego przez każdy element wzrasta divided (współdzielone) między sobą od prądu, który wchodzi do węzła.
Rozważ następujące circuit diagram.
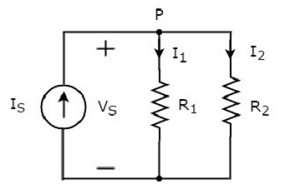
Powyższy schemat obwodu składa się ze źródła prądu wejściowego IS równolegle z dwoma rezystorami R1 i R2. Napięcie na każdym elemencie wynosiVS. Prądy przepływające przez rezystoryR1 i R2 są I1 i I2 odpowiednio.
Plik KCL equation w węźle P będzie
$$ I_S = I_1 + I_2 $$
Podstaw $ I_1 = \ frac {V_S} {R_1} $ i $ I_2 = \ frac {V_S} {R_2} $ w powyższym równaniu.
$$ I_S = \ frac {V_S} {R_1} + \ frac {V_S} {R_2} = V_S \ lgroup \ frac {R_2 + R_1} {R_1 R_2} \ rgroup $$
$$ \ Rightarrow V_S = I_S \ lgroup \ frac {R_1R_2} {R_1 + R_2} \ rgroup $$
Zastąp wartość V S w $ I_1 = \ frac {V_S} {R_1} $.
$$ I_1 = \ frac {I_S} {R_1} \ lgroup \ frac {R_1 R_2} {R_1 + R_2} \ rgroup $$
$$ \ Rightarrow I_1 = I_S \ lgroup \ frac {R_2} {R_1 + R_2} \ rgroup $$
Zastąp wartość V S w $ I_2 = \ frac {V_S} {R_2} $.
$$ I_2 = \ frac {I_S} {R_2} \ lgroup \ frac {R_1 R_2} {R_1 + R_2} \ rgroup $$
$$ \ Rightarrow I_2 = I_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
Z równań I 1 i I 2 możemy uogólnić, że prąd płynący przez dowolny element pasywny można znaleźć za pomocą następującego wzoru.
$$ I_N = I_S \ lgroup \ frac {Z_1 \ rVert Z_2 \ rVert ... \ rVert Z_ {N-1}} {Z_1 + Z_2 + ... + Z_N} \ rgroup $$
Jest to znane jako current division principle i ma to zastosowanie, gdy dwa lub więcej elementów pasywnych jest połączonych równolegle i tylko jeden prąd wpływa do węzła.
Gdzie,
I N jest prąd płynący przez bierny element N -tego oddziału.
I S to prąd wejściowy, który wchodzi do węzła.
Z 1 , Z 2 , ..., Z N są impedancje 1 st oddziału, 2 nd oddziału, ..., n th oddział odpowiednio.
Zasada podziału napięcia
Kiedy dwa lub więcej elementów pasywnych jest połączonych szeregowo, wartość napięcia obecnego na każdym elemencie wzrasta divided (współdzielone) między sobą z napięcia, które jest dostępne w całej tej kombinacji.
Rozważ następujące circuit diagram.
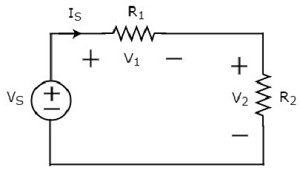
Powyższy schemat obwodu składa się ze źródła napięcia V S połączonego szeregowo z dwoma rezystorami R 1 i R 2 . Prąd płynący przez te elementy ja S . Spadki napięcia na rezystorach R 1 i R 2 wynoszą odpowiednio V 1 i V 2 .
Plik KVL equation wokół pętli będzie
$$ V_S = V_1 + V_2 $$
Podstawienie V 1 = I S R 1 i V 2 = I S R 2 w powyższym równaniu
$$ V_S = I_S R_1 + I_S R_2 = I_S (R_1 + R_2) $$
$$ I_S = \ frac {V_S} {R_1 + R_2} $$
Zastąp wartość I S w V 1 = I S R 1 .
$$ V_1 = \ lgroup \ frac {V_S} {R_1 + R_2} \ rgroup R_1 $$
$$ \ Rightarrow V_1 = V_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
Zastąp wartość I S w V 2 = I S R 2 .
$$ V_2 = \ lgroup \ frac {V_S} {R_1 + R_2} \ rgroup R_2 $$
$$ \ Rightarrow V_2 = V_S \ lgroup \ frac {R_2} {R_1 + R_2} \ rgroup $$
Z równań V 1 i V 2 możemy uogólnić, że napięcie na dowolnym elemencie pasywnym można znaleźć za pomocą następującego wzoru.
$$ V_N = V_S \ lgroup \ frac {Z_N} {Z_1 + Z_2 + .... + Z_N} \ rgroup $$
Jest to znane jako voltage division principle i ma zastosowanie, gdy dwa lub więcej elementów pasywnych jest połączonych szeregowo i tylko jedno napięcie jest dostępne w całej kombinacji.
Gdzie,
V N jest napięciem na N- tym elemencie pasywnym.
V S jest napięciem wejściowym, które występuje w całej kombinacji szeregowych elementów pasywnych.
Z 1 , Z 2 , ..., Z 3 są impedancje 1 st elementu biernego, 2 nd biernego elementu, ..., n -tego elementu pasywnego odpowiednio.