Teoria sieci - rezonans równoległy
W poprzednim rozdziale omówiliśmy znaczenie rezonansu szeregowego. Omówmy teraz rezonans równoległy w obwodach RLC.
Schemat równoległego obwodu rezonansowego
Jeśli rezonans występuje w równoległym obwodzie RLC, nazywa się go as Parallel Resonance. Rozważ następująceparallel RLC circuit, który jest reprezentowany w dziedzinie wskazowej.
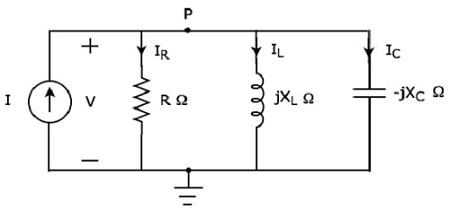
Tutaj elementy bierne, takie jak rezystor, cewka i kondensator, są połączone równolegle. Ta cała kombinacja jest dostępnaparallel z wejściowym źródłem prądu sinusoidalnego.
pisać nodal equation w węźle P.
$$ - I + I_R + I_L + I_C = 0 $$
$$ \ Rightarrow - I + \ frac {V} {R} + \ frac {V} {j X_L} + \ frac {V} {- j X_C} = 0 $$
$$ \ Rightarrow I = \ frac {V} {R} - \ frac {jV} {X_L} + \ frac {jV} {X_C} $$
$ \ Rightarrow I = V [\ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup] $Equation 1
Powyższe równanie ma postać I = VY.
Dlatego też admittance Y równoległego obwodu RLC
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup $$
Parametry i wielkości elektryczne w rezonansie
Teraz wyprowadźmy kolejno wartości parametrów i wielkości elektrycznych przy rezonansie równoległego obwodu RLC.
Częstotliwość rezonansowa
Wiemy, że resonant frequency, frjest częstotliwością, przy której występuje rezonans. Równolegle rezonans obwodu RLC występuje, gdy wyimaginowany człon admitancji Y wynosi zero. tj. wartość $ \ frac {1} {X_C} - \ frac {1} {X_L} $ powinna być równa zero
$$ \ Rightarrow \ frac {1} {X_C} = \ frac {1} {X_L} $$
$$ \ Rightarrow X_L = X_C $$
Powyższy stan rezonansu jest taki sam, jak w przypadku obwodu szeregowego RLC. Tak więcresonant frequency, fr będzie taki sam w obwodzie szeregowym RLC i równoległym obwodzie RLC.
Dlatego też resonant frequency, fr równoległego obwodu RLC
$$ f_r = \ frac {1} {2 \ pi \ sqrt {LC}} $$
Gdzie,
- L to indukcyjność cewki indukcyjnej.
- C jest pojemnością kondensatora.
Plik resonant frequency, fr równoległego obwodu RLC zależy tylko od indukcyjności L i pojemność C. Ale jest niezależny od oporuR.
Wstęp
Mamy admittance Y równoległego obwodu RLC jako
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup $$
Zastąp $ X_L = X_C $ w powyższym równaniu.
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_C} \ rgroup $$
$$ \ Rightarrow Y = \ frac {1} {R} + j (0) $$
$$ \ Rightarrow Y = \ frac {1} {R} $$
W rezonansie admittance, Y równoległego obwodu RLC jest równe odwrotności oporu, R. tj. $ \ Mathbf {\ mathit {Y = \ frac {1} {R}}} $
Napięcie na każdym elemencie
Podstaw, $ \ frac {1} {X_C} - \ frac {1} {X_L} = 0 $ w równaniu 1
$$ I = V [\ frac {1} {R} + j (0)] $$
$$ \ Rightarrow I = \ frac {V} {R} $$
$$ \ Rightarrow V = IR $$
Dlatego też voltage na wszystkich elementach równoległego obwodu RLC w rezonansie V = IR.
Przy rezonansie admitancja równoległego obwodu RLC osiąga wartość minimalną. W związku z tym,maximum voltage jest obecny w każdym elemencie tego obwodu w rezonansie.
Prąd przepływający przez rezystor
Prąd przepływający przez rezystor wynosi
$$ I_R = \ frac {V} {R} $$
Zastąp wartość V w powyższym równaniu.
$$ I_R = \ frac {IR} {R} $$
$$ \ Rightarrow I_R = I $$
Dlatego też current flowing through resistor przy rezonansie to $ \ mathbf {\ mathit {I_R = I}} $.
Prąd przepływający przez cewkę indukcyjną
Prąd przepływający przez cewkę wynosi
$$ I_L = \ frac {V} {j X_L} $$
Zastąp wartość V w powyższym równaniu.
$$ I_L = \ frac {IR} {j X_L} $$
$$ \ Rightarrow I_L = -j \ lgroup \ frac {R} {X_L} \ rgroup I $$
$$ \ Rightarrow I_L = -jQI $$
Dlatego też current flowing through inductor przy rezonansie wynosi $ I_L = -jQI $.
Tak więc magnitude prądu przepływającego przez cewkę w rezonansie będzie
$$ | I_L | = QI $$
Gdzie Q jest Quality factor a jego wartość jest równa $ \ frac {R} {X_L} $
Prąd przepływający przez kondensator
Prąd przepływający przez kondensator wynosi
$$ I_C = \ frac {V} {- j X_C} $$
Zastąp wartość V w powyższym równaniu.
$$ I_C = \ frac {IR} {- j X_C} $$
$$ \ Rightarrow I_C = j \ lgroup \ frac {R} {X_C} \ rgroup I $$
$$ \ Rightarrow I_C = jQI $$
Dlatego też current flowing through capacitor przy rezonansie wynosi $ I_C = jQI $
Tak więc magnitude prądu przepływającego przez kondensator w rezonansie wyniesie
$$ | I_C | = QI $$
Gdzie Q jest Quality factor a jego wartość jest równa $ \ frac {R} {X_C} $
Note - Równoległy obwód rezonansowy RLC nazywa się current magnificationobwód. Ponieważ wielkość prądu przepływającego przez cewkę i kondensator jest równa Q razy wejściowy prąd sinusoidalny I .